ACUSTICA

Acustica

(I, p. 453; App. I, p. 21; II, i, p. 23; III, i, p. 16; IV, i, p. 27; V, 1, p. 33)

a. fisica

Le questioni relative alla storia dell'a., all'a. fisica in generale e all'a. musicale sono state trattate nella voce suono (XXXII, p. 995), mentre quelle di a. ambientale hanno trovato una trattazione sistematica in tutti gli articoli dedicati all'a. nel vol. I dell'Enciclopedia e nelle Appendici successive. Gli argomenti relativi all'a. medica sono trattati in sordità (XXXII, p. 156; App. V, v, p. 334) e udito (XXXIV, p. 605; App. V, v, p. 619). Per una disciplina applicata come l'elettroacustica, riguardante la trasduzione da segnali acustici a segnali elettrici oppure di altra natura (per es., meccanici e magnetici), e viceversa, nonché per la manipolazione di tali segnali, in particolare le tecniche di registrazione e di riproduzione dei suoni, v. la voce suono nel vol. XXXII (p. 995) e nelle Appendici III, ii, p. 872; IV, iii, p. 545; V, v, p. 334. *

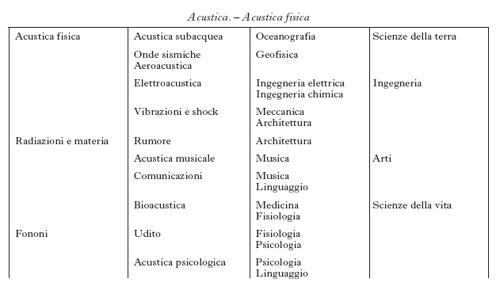
L'a., originariamente limitata allo studio delle sensazioni fisiologiche prodotte sull'orecchio umano dalle vibrazioni propagantisi nel mezzo aeriforme con cui esso viene a contatto, è divenuta successivamente tipico oggetto di studio della fisica, quale estensione della meccanica dei continui, nella consueta ipotesi che la lunghezza d'onda della radiazione d'interesse sia di molti ordini di grandezza superiore alle dimensioni delle strutture microscopiche costituenti il mezzo di propagazione. Come tale, si può dire che l'a. come disciplina si sia consolidata già nel 19° sec. in modo pressoché definitivo; nel corso del 20° sec., tuttavia, l'importanza assunta prima dalle telecomunicazioni, poi dall'elettronica e dalla microelettronica in generale, ha esteso le possibilità di applicazioni dell'a. a onde elastiche di frequenza ben al di sopra del limite di udibilità e quindi a tecnologie e settori scientifici nuovi. Inoltre, i risultati conseguiti in questi nuovi settori hanno permesso di rilanciare le applicazioni già note a nuovi indirizzi di ricerca e a nuovi campi di indagine: alle basse temperature, ai film sottili e alle microstrutture in genere, ai semiconduttori, a tutti i nuovi tipi di materiali ecc. In pari tempo, si sono aggiornate e ampliate le conoscenze della fisiologia dell'orecchio, della psicoacustica, dell'a. architettonica, così che le interconnessioni dell'a. con le varie scienze e, più in generale, con le varie attività dell'uomo si sono moltiplicate e non appare semplice fornire un quadro organico di sintesi cui riferire i risultati più recenti. Può ancora, in questo senso, costituire un utile riferimento il quadro descrittivo qui riprodotto, dove, procedendo da sinistra verso destra, si accentua il carattere più applicativo dell'argomento ed è sempre più presente l'interesse per l'uomo a mano a mano che si considerino settori posti più in basso. Dallo schema riportato si deduce che, se pure l'a. trova i suoi naturali riferimenti nella fisica di base e nelle interazioni tra i campi elastici e la materia, i temi della propagazione di onde elastiche sono diffusi in moltissimi altri campi.

Più che la consueta identificazione e suddivisione dei temi per campi di frequenze, può aiutare a individuare un ordine tra le diverse problematiche la semplice analisi diretta dell'oggetto di studio della disciplina, cioè l'onda elastica rappresentata, per questo scopo, mediante l'espressione consueta di un'onda piana sinusoidale a distanza r dall'origine delle coordinate spaziali e all'istante t:

a(r,t)=A(r,t)exp[i(k∙r±ωt)+φ]

con i unità immaginaria, caratterizzata da un'ampiezza A del campo acustico (che può rappresentare una qualunque grandezza fisica caratteristica della propagazione), un vettore d'onda k (il cui modulo è la pulsazione spaziale k=2π/λ, con λ lunghezza d'onda, da vedersi anche come periodo spaziale), una pulsazione temporale ω (=2π/T, con T periodo temporale) e una fase di riferimento φ (la fase che si ha per r=t=0).

Al legame funzionale k(ω) tra k e ω sono riconducibili le problematiche più strettamente connesse con la struttura della materia e con la fisica dei materiali. Velocità e assorbimento dell'onda, parametri legati, rispettivamente, alla parte reale e immaginaria della funzione k(ω), sono infatti intimamente dipendenti dall'interazione tra l'onda, o i quanti dell'energia acustica (fononi), e la struttura microscopica del mezzo di propagazione, che nella teoria del continuo non viene esplicitamente considerata. Di qui si possono ricavare informazioni relative alle dimensioni e distribuzioni spaziali di strutture o microstrutture presenti come inclusioni o disperse all'interno di un mezzo, sui materiali stratificati e i materiali compositi.

Al modo di propagarsi di un'onda o di un fronte d'onda in un mezzo, cioè allo studio della funzione k(r), è volto l'interesse di una serie di discipline applicate che fanno uso della propagazione elastica come mezzo di informazione per localizzare ostacoli o determinare la forma di oggetti presenti in un mezzo, generalmente omogeneo, di propagazione. Dai primi studi di L. Spallanzani sull'orientamento dei pipistrelli per ecolocalizzazione in volo degli ostacoli mediante il suono, lo sviluppo di tecniche volte agli scopi anzidetti, spesso chiamate di imaging, ha compiuto progressi notevolissimi. Ricorderemo che esempi di utilizzazione dell'a., sempre più frequenti e di migliore resa, sono: la determinazione della forma dei fondali e delle coste; nell'oceanografia, la localizzazione dei banchi di pesci, di ostacoli; nella medicina, in varie tecniche ecografiche, integrative o sostitutive di quelle a raggi X, l'esame di organi o tessuti; la rivelazione di sedimenti e giacimenti nella prospezione geofisica come anche l'individuazione di oggetti di interesse archeologico sepolti nel sottosuolo; nella microscopia, la visualizzazione di strutture opache alla luce, di interesse biologico o in uso nella microelettronica; nelle varie tecnologie di fabbricazione, l'analisi on-line di prodotti, per l'individuazione di scarti o difetti di processi. In ciascuna di queste applicazioni, sia pure a frequenze diverse e attraverso l'impiego di tecniche diverse, il meccanismo fondamentale di ricostruzione dell'immagine consiste nella rivelazione e nel trattamento del segnale prodotto dall'eco acustica riflessa dalle superfici di discontinuità costituite dalle differenti caratteristiche elastiche presenti nel mezzo, alle quali corrispondono variazioni di impedenza acustica; queste determinano variazioni locali del vettore d'onda k, che vengono analizzate come segnali da un'opportuna catena di rivelazione elettronica. Occorre notare come in questa fenomenologia, negli esempi applicativi indicati, le lunghezze d'onda coinvolte spazino su più di cinque ordini di grandezza: da valori di decine di metri, per es., nelle misurazioni delle distanze dei fondali in oceanografia, a qualche μm, nell'analisi microscopica dei microchip elettronici.

Infine, alla funzione A(t), descrivente la dipendenza dell'ampiezza del campo dal tempo, fanno capo le numerose applicazioni che l'elettronica e le tecniche del trattamento del segnale hanno sviluppato, fondate sulla propagazione delle onde elastiche. Più frequente è, in questo campo, l'uso di onde di elevata frequenza, tipicamente dell'ordine delle decine di MHz fino a qualche GHz, assai spesso propagantisi come onde elastiche superficiali sulla superficie di cristalli. Le applicazioni in questo campo passano necessariamente attraverso la realizzazione di un dispositivo di tipo analogico dove un trasduttore elettroacustico trasforma il segnale elettrico in un'onda elastica e un secondo la ritrasforma in segnale elettrico, dopo l'opportuna variazione avvenuta nel mezzo. L'interesse per questi dispositivi deriva essenzialmente dal basso valore della velocità di propagazione dell'onda acustica rispetto a quella di un'onda elettromagnetica, inferiore di circa cinque ordini di grandezza, che permette di realizzare linee di ritardo di limitate dimensioni e con limitate perdite di inserzione. Negli ultimi decenni, l'introduzione dei trasduttori interdigitali ha consentito di realizzare dispositivi a onde elastiche superficiali, nei quali la disponibilità del segnale acustico lungo il cammino di propagazione ne permette l'analisi e la modificazione, e quindi la riconduzione a segnale elettrico per un opportuno trattamento. Con tali tecniche si realizzano tipicamente, oltre a linee di ritardo, come già indicato, filtri di frequenza, dispositivi elettroacustici o anche acusto-ottici per l'analisi spettrale di un segnale ecc.

Ancora riconducibile all'analisi temporale del segnale, quindi alla funzione A(t) citata sopra, è l'ampio campo delle non linearità acustiche, che promette quasi di costituire una disciplina a sé stante (v. acustica non lineare, App. V), vuoi per le implicazioni teoriche, oltre che pratiche, che hanno assunto alcuni temi specifici, come quelli dei solitoni, delle biforcazioni, del caos e altri, conseguenti ai fenomeni non lineari, vuoi però anche e soprattutto per l'incidenza che ha oggi l'ipotesi di non linearità tout-court in ogni ambito della fisica e nelle discipline scientifiche in genere. La propagazione acustica costituisce per il fenomeno della non linearità un processo secolare, che si estende cioè su una scala temporale molto estesa, nel senso che la generazione locale di un'onda armonica lungo la propagazione per effetto di termini non lineari nell'equazione delle onde e la non dispersività del mezzo per frequenze sufficientemente alte, portano a sommare in fase il nuovo contributo all'effetto cumulativo fino a quel momento prodottosi. La stessa fenomenologia ha luogo nel tempo in un risonatore non lineare. Sono fenomeni coinvolgenti il regime di non linearità delle onde i suoni emessi da strumenti musicali in regime di forte o fortissimo; sono frutto di non linearità i fenomeni di sonoluminescenza prodotti nelle oscillazioni delle bolle di cavitazione in liquidi irradiati; è effetto di non linearità la generazione di frequenze subarmoniche nelle vibrazioni di strutture meccaniche o di generatori, con le implicazioni di processi a soglia e la generazione a cascata di frequenze sottomultiple fino alla produzione di fenomeni caotici; passa necessariamente attraverso lo sfruttamento di fenomeni non lineari la possibilità di effettuare un controllo attivo del rumore attraverso un mescolamento di onde coniugate in fase.

bibliografia

W. Yost, D.W. Nielsen, Fundamentals of hearing. An introduction, New York 1977, 1985²; H. Kuttruff, Ultrasonics. Fundamentals and applications, London-New York 1991. Cfr. inoltre dal 1964 in poi Physical acoustics, New York, poi San Diego, collana in continua pubblicazione per l'aggiornamento della disciplina.