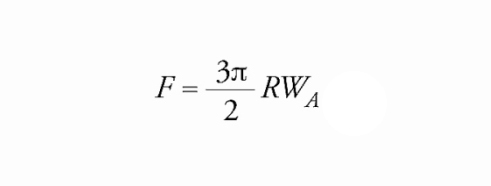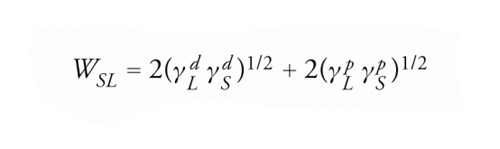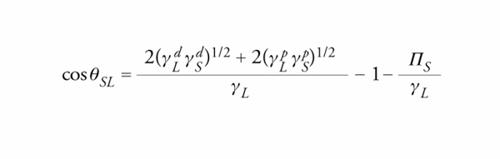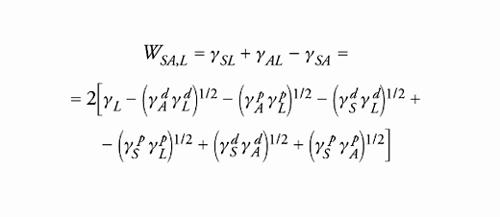Adesione

Adesione

Il fenomeno per cui due oggetti messi a contatto, si attraggono reciprocamente e hanno la tendenza a restare attaccati l'uno all'altro è chiamato adesione, o, se interessa due parti dello stesso corpo, coesione. Pur verificandosi sistematicamente, tale fenomeno spesso è poco evidente: nella maggior parte dei casi, gli oggetti con cui abbiamo a che fare non aderiscono spontaneamente l'uno all'altro, perché l'intensità delle forze in gioco è molto piccola. L'adesione, infatti, è dovuta a interazioni il cui raggio d'azione è dell'ordine delle distanze intermolecolari: legami fisici ‒ forze intermolecolari ‒ tra le superfici dei corpi a contatto e, talora, anche veri e propri legami chimici tra molecole appartenenti a corpi diversi. Affinché due oggetti macroscopici aderiscano con un'intensità apprezzabile, tra di essi si deve perciò stabilire un contatto a livello microscopico. Motivi di ordine meccanico, dovuti alle irregolarità della superficie, e le impurezze che si frappongono tra le molecole, prima fra tutte l'umidità, rendono però tale contatto difficilmente realizzabile tra due solidi; d'altra parte, alcuni esperimenti hanno mostrato che, se la distanza di separazione scende al di sotto di un valore critico ‒ tipicamente tra 1 e 10 nm ‒ campioni di mica, oro, gomma e gelatina, lisci su scala atomica, aderiscono spontaneamente l'uno all'altro. Diverso è il caso di un liquido e un solido, tra i quali è facile che si stabilisca un contatto molecolare che rende l'adesione molto intensa; ne sono una dimostrazione i fenomeni di capillarità, o il fatto stesso che i liquidi bagnano i solidi. Per la maggior parte, gli adesivi utilizzati comunemente nell'industria e nella vita quotidiana si trovano nella fase liquida al momento dell'applicazione e soltanto in seguito solidificano, proprio perché possano bagnare adeguatamente il substrato e successivamente aumentare la propria coesione: tra i numerosi esempi possiamo citare le colle viniliche, che, applicate in emulsione acquosa, solidificano in seguito all'evaporazione del mezzo liquido, e gli adesivi universali istantanei a base di cianoacrilati, i quali polimerizzano molto rapidamente in presenza di umidità sul substrato.

L'adesione ha notevole importanza anche in biologia cellulare, in quanto rappresenta il meccanismo con cui le cellule si uniscono tra loro o con la matrice extracellulare, particolari proteine, dette molecole di adesione, rivestono un ruolo fondamentale nella formazione di tessuti e di organi durante l'embriogenesi, nella risposta immunitaria e nello sviluppo di alcune malattie quali i tumori. Sono soprattutto le applicazioni tecnologiche, però, prima fra tutte l'incollaggio, che alimentano l'interesse verso l'adesione. Tra i maggiori consumatori di adesivi troviamo industrie ad alta tecnologia quali l'aeronautica, l'aerospaziale, l'automobilistica e l'elettronica, in cui saldature e rivettature sono state parzialmente sostituite da giunzioni adesive, che permettono di unire facilmente tra loro materiali diversi, assicurano una distribuzione degli sforzi più uniforme e sono più resistenti alla fatica, oltre a essere più leggere e migliori dal punto di vista estetico. Gli adesivi trovano largo impiego anche nell'industria del legno, delle costruzioni, delle calzature, dell'imballaggio, dello sport, ecc.; più recentemente il loro uso è stato introdotto anche in odontoiatria e in chirurgia. Una conoscenza approfondita dell'adesione, oltre a permettere di migliorare la qualità degli adesivi, è utile nella realizzazione di quei prodotti ‒ vernici, rivestimenti, materiali compositi, ecc. ‒ le cui prestazioni dipendono dalle proprietà dell'interfaccia tra due materiali.

Scienza dell'adesione

Le origini della scienza dell'adesione risalgono ai primi studi sulle forze intermolecolari e sulla meccanica della frattura, ma è soltanto a partire dagli anni Settanta del XX sec. che tale disciplina si è guadagnata una propria autonomia. Pur essendosi sempre trovata in posizione secondaria rispetto alle applicazioni tecnologiche, negli ultimi anni il divario tra la scienza e la tecnologia dell'adesione si sta riducendo rapidamente. L'adesione è un fenomeno complesso, che coinvolge svariate discipline, quali la chimica fisica delle superfici e delle interfacce, la scienza delle macromolecole, la scienza dei materiali, la reologia e la meccanica della frattura, e che risulta perciò difficile da comprendere nella sua generalità. L'approccio al problema può variare a seconda dello scopo che ci si prefigge: se si tratta di studiare le forze intermolecolari all'origine dell'attrazione tra i corpi, esso sarà di tipo microscopico; in questo contesto l'adesione è detta fondamentale ed è quantificata dal lavoro termodinamico di adesione W_A, che è definito come il lavoro per unità di superficie necessario per separare reversibilmente due corpi e che assume tipicamente valori dell'ordine di 10⁻¹÷10⁻² J/m². Qualora si sia interessati invece alla resistenza di un giunto, è necessario analizzare la rottura del legame adesivo, processo che coinvolge oggetti macroscopici.

L'adesione fondamentale

fig. 2

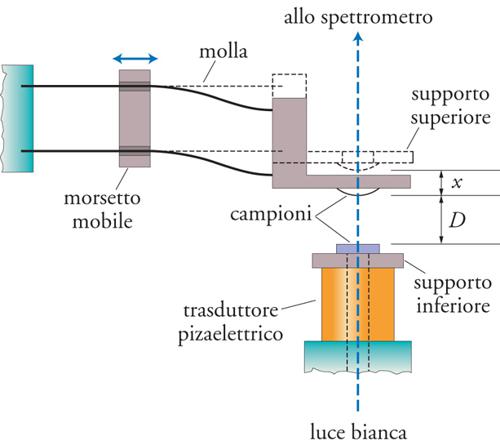
Il lavoro termodinamico di adesione si può ricavare dalla misurazione diretta delle forze intermolecolari se si è in presenza di due solidi, da misurazioni di angolo di contatto se si hanno un solido e un liquido. Nel primo caso, per valutare la forza di disimpegno F (pull-off force), ossia la minima forza necessaria per separare due solidi posti a contatto, si può ricorrere al cosiddetto SFA (Surface force apparatus), sviluppato da David Tabor, Richard H.S. Winterton e Jacob N. Israelachvili e in grado di misurare forze dell'ordine di 10⁻⁸ N a distanze di separazione di frazioni di nanometro (fig. 2). La teoria di Johnson, Kendall e Roberts (JKR), che nel caso di due solidi elastici permette di ricavare il lavoro termodinamico di adesione, prevede che per due sfere di uguale raggio R valga la seguente relazione:

[1] formula.

La [1] implica, per esempio, che la forza necessaria a separare due sfere solide di raggio R=1 cm per le quali il lavoro di adesione vale W_A=10⁻² J/m² è di soli 0,5 mN; dal confronto con la forza esercitata dall'attrazione gravitazionale terrestre, che se le due sfere sono dense quanto l'acqua vale circa 40 mN, risulta evidente per quale motivo l'adesione tra solidi possa essere trascurata su scala macroscopica. Al diminuire del raggio delle sfere, però, la forza di disimpegno decresce molto più lentamente rispetto alla forza di gravità, in quanto l'una è proporzionale a R e l'altra a R³, cosicché per particelle sufficientemente piccole l'adesione domina sull'attrazione gravitazionale.

Nel caso di adesivi liquidi su substrati solidi, possiamo affermare che una condizione necessaria perché si realizzi l'adesione è che l'adesivo bagni il substrato, in modo da realizzare a livello microscopico un contatto che permetta alle forze intermolecolari di agire. Le misurazioni dell'angolo di contatto, importanti al fine di ricavare il lavoro termodinamico di adesione, saranno trattate dettagliatamente nel paragrafo in cui studieremo gli aspetti termodinamici dell'interfaccia adesivo-substrato e ne descriveremo la teoria.

L'adesione pratica

Completamente diverso dal precedente è il problema di determinare la resistenza di un giunto adesivo. Perché un giunto adesivo sia resistente, bisogna che i materiali che lo costituiscono siano in grado di dissipare grandi quantità di energia in maniera viscoelastica o plastica; per questo la reologia dell'adesione assume un ruolo fondamentale nella progettazione dei giunti. La reologia, così come d'altra parte la termodinamica dell'interfaccia, è un aspetto assai generale, che permette di interpretare una gran quantità di fenomeni adesivi; le teorie che la descrivono saranno trattate nel seguito.

fig. 3

L'entità dell'adesione cosiddetta pratica è valutata in relazione a una grandezza macroscopica: l'energia di frattura adesiva G_a, definita come il lavoro necessario a separare una superficie dell'interfaccia del giunto che abbia estensione unitaria. È misurata in prove di frattura (fig. 3) e può valere fino a 10²÷10⁴ J/m². Il suo valore dipende in maniera sostanziale dal tipo di prova e dalle condizioni in cui questa si svolge: a incidere sono soprattutto la velocità v di propagazione della frattura e la temperatura T. Da un rapido confronto si nota che G_a è fino a un milione di volte maggiore di W_A, e questo perché la maggior parte dell'energia spesa per rompere una giunzione è dissipata viscoelasticamente o plasticamente dall'adesivo, piuttosto che essere impiegata per rompere il legame adesivo all'interfaccia; gran parte degli adesivi sono infatti elastomeri o termoplastici, ossia sono composti da materiali capaci di deformarsi e di assorbire enormi quantità di energia prima di cedere.

L'energia di frattura è la quantità che riveste maggiore interesse nelle applicazioni tecnologiche dell'adesione, ma purtroppo può essere misurata esclusivamente mediante prove distruttive: questa circostanza rappresenta uno degli svantaggi dell'incollaggio rispetto ad altri tipi di giunzioni ed è uno dei motivi per cui è importante avere a disposizione modelli teorici che forniscano la G_a di un giunto senza doverlo rompere.

Teorie dell'adesione

La scienza dell'adesione è, come abbiamo visto, una disciplina piuttosto recente, che si occupa di un fenomeno affatto complesso, e non deve quindi stupire che non esista un'unica teoria dell'adesione. Si può dire che quasi ogni coppia di materiali rappresenti un caso particolare, da descrivere attraverso un modello specifico, ma il fatto che esistano alcuni tratti comuni a più sistemi ha portato a formulare teorie in grado di stabilire criteri di buona adesione per intere classi di materiali. Come già accennato, aspetti molto generali sono la termodinamica e la reologia, che permettono di interpretare una gran quantità di fenomeni adesivi. Meno universale, ma ugualmente degno attenzione, è il ruolo dei legami chimici, che allorquando siano presenti contribuiscono notevolmente alla tenuta di un'interfaccia. È ormai superata invece la teoria elettrostatica, che all'origine dell'adesione invocava un trasferimento di elettroni tra adesivo e substrato: è applicabile solamente in pochissimi casi e trascura completamente gli aspetti reologici.

Aspetti termodinamici

La teoria termodinamica ha validità molto generale, dovuta al fatto che le forze dispersive di London sono universalmente presenti, ed è una delle più diffuse nello studio dell'adesione. La prima formulazione di una teoria termodinamica dell'adesione si deve a Louis Houghton Sharpe e Harold Schonhorn e si basa sull'ipotesi che le interazioni fisiche tra molecole siano sufficienti a generare l'adesione tra due materiali. Tali forze, per poter essere efficaci, richiedono che adesivo e substrato siano in intimo contatto, ciò che, di solito, avviene se l'adesivo è applicato in forma liquida su un substrato solido; condizione necessaria perché ci sia adesione è perciò che l'adesivo bagni il substrato. Nel descrivere il processo di bagnatura, la teoria termodinamica stabilisce alcuni criteri di bagnabilità e mette in relazione il lavoro termodinamico di adesione con le energie superficiali dei singoli materiali, tanto che tale teoria è anche nota come modello di bagnatura (wetting model).

Il lavoro termodinamico di adesione, che indicheremo con W_SL per ricordare che stiamo considerando un'interfaccia solido-liquido, è dato dall'equazione di Dupré

[2] W_SL = γ_S + γ_L − γ_SL

fig. 4

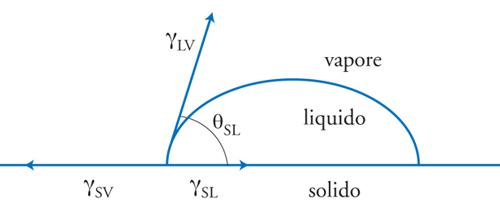
che esprime la differenza di energia tra lo stato in cui le due superfici sono separate nel vuoto e quello in cui esse sono a contatto. Le grandezze γ_S, γ_L e γ_SL sono le energie libere superficiali rispettivamente del solido, del liquido e dell'interfaccia tra i due. L'energia di coesione di un materiale si ottiene applicando la [2] a due mezzi identici ed è uguale al doppio dell'energia superficiale. Consideriamo adesso una goccia di liquido in equilibrio con il suo vapore, appoggiata su un substrato solido come indicato nella fig. 4. Dall'equazione di Young, ricordando che per un liquido γ_LV=γ_L, si ottiene immediatamente l'equazione di Young-Dupré

[3] W_SL = γ_L (1 + cosθ_SL)+ Π_S,

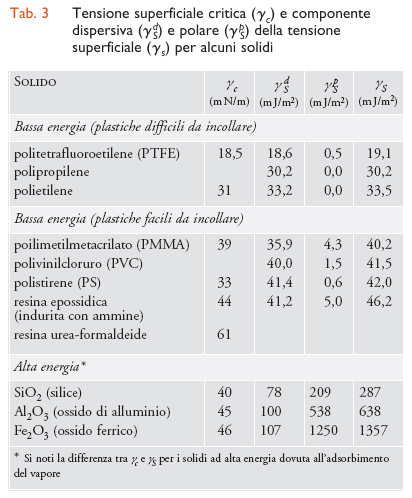
dove Π_S è la pressione di spargimento (spreading pressure) dovuta all'adsorbimento del vapore sul solido, definita dalla relazione γ_SV=γ_S−Π_S. La [3] mette in relazione il lavoro termodinamico di adesione con l'angolo di contatto θ_SL tra adesivo e substrato. Per i solidi a bassa energia superficiale (γ_S〈100 mJ/m²), come per esempio i polimeri, si può assumere Π_S=0; il lavoro di adesione si può ricavare dalla [3] e da misurazioni dell'angolo di contatto, una volta supposta nota la tensione superficiale dell'adesivo, che può essere misurata indipendentemente. I solidi caratterizzati da elevati valori dell'energia superficiale (γ_S>500 mJ/m²), quali metalli e ossidi, sono invece bagnati spontaneamente dalla maggior parte dei liquidi di prova, cosicché diviene impossibile la misurazione dell'angolo di contatto. Un metodo alternativo consiste nel misurare la pressione di spargimento Π_S e nel ricavare il lavoro termodinamico di adesione mediante la [3], che per θ_SL=0 diventa W_SL=2γ_L+Π_S. Poiché per θ_SL=0 un liquido bagna completamente un solido, dalla [3] si ottiene la seguente condizione per avere bagnabilità:

[4] W_SL ≥ 2γ_L + Π_S;

la [4] richiede che il bilancio energetico a seguito del processo di bagnatura sia positivo. Per solidi a bassa energia si ha Π_S=0 e il criterio di bagnabilità [4] impone semplicemente che l'energia di adesione solido-liquido sia maggiore dell'energia di coesione del liquido. La [2] e la [4] permettono di stabilire se un adesivo bagnerà il substrato e quanto intensa sarà l'adesione tra i due; perciò, riscritte in funzione di grandezze relative ai singoli corpi, esse consentono di valutare l'adesione tra due qualunque materiali in base alle caratteristiche individuali di questi ultimi.

fig. 5

In un lavoro divenuto classico, William Albert Zisman ha osservato che, per un dato solido, cosθ_SL è proporzionale a γ_L. Ha introdotto inoltre una tensione superficiale critica γ_C, caratteristica del solido, corrispondente alla tensione superficiale di un liquido per il quale θ_SL=0. Riportando in un grafico cosθ_SL in funzione di γ_L si può quindi ricavare γ_C estrapolando, o misurando, quel valore di γ_L per cui cosθ_SL=1, come mostrato in fig. 5; il criterio di bagnabilità diventa allora

[5] γ_C ≥ γ_L .

L'energia superficiale critica è una grandezza empirica legata alla tensione superficiale del solido, di notevole utilità pratica perché permette di prevedere immediatamente se un liquido bagnerà o meno un solido. È inoltre possibile generalizzare questo modello al caso di due solidi, di cui uno liquido al momento dell'applicazione, e, confrontando le due energie superficiali critiche, prevedere se l'uno bagnerà l'altro. In particolare, se ne può concludere che se il primo solido bagna il secondo, allora non potrà mai accadere che il secondo bagni il primo. Per esempio, sebbene non si produca adesione polimerizzando una resina epossidica (γ_C=44 mJ/m²) su polietilene (γ_C=31 mJ/m²), applicando su una resina epossidica precedentemente polimerizzata polietilene fuso si ottiene un'ottima adesione.

Con un'analisi più rigorosa Frederick Mayhew Fowkes ha suggerito che tanto il lavoro di adesione quanto la tensione superficiale possano essere scritti come la somma di vari termini dovuti ai diversi tipi di interazioni molecolari, ipotizzando inoltre che, se agiscono esclusivamente forze di tipo dispersivo, l'energia di interazione tra due superfici sia data dalla media geometrica delle rispettive energie superficiali. Per analogia D.K. Owens e R.C. Wendt e, successivamente, D.H. Kaelble hanno proposto di estendere il metodo della media geometrica anche alle componenti non dispersive delle tensioni superficiali, ottenendo

[6] formula

e, dalla [3],

[7] formula

2

3

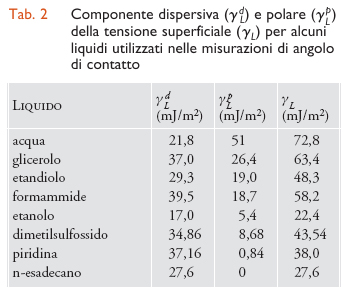
dove gli apici d e p indicano rispettivamente le componenti dispersive e polari della tensione superficiale γ=γ^d+γ^p. In questo modello, di uso assai frequente per via della sua semplicità, la componente polare include sia le interazioni di Debye e Keesom, sia il legame a idrogeno e l'interazione acido-base di Lewis; nelle tabb. 2 e 3 sono riportate rispettivamente le energie superficiali di alcuni liquidi e alcuni solidi. Confrontanto la [7] con la teoria di Zisman, emerge che il valore della tensione critica dipende dai liquidi usati per la misurazione; per esempio, per solidi a bassa energia (Π_S=0) che si trovino a contatto con liquidi apolari (γ_L^p=0) si ottiene γ_C=γ_S^d , relazione che però non è verificata nel caso di liquidi polari. Una volta note le tensioni superficiali, possiamo calcolare il lavoro di adesione per qualunque coppia di materiali in diversi ambienti; a tal fine, se un giunto è collocato nel vuoto o in aria asciutta è necessario applicare la [6], mentre se è immerso in un liquido vale la relazione

[8] formula

tab. 4

dove i pedici A, S e L indicano rispettivamente l'adesivo, il substrato e l'ambiente liquido. I risultati sperimentali ottenuti per alcune coppie di materiali in diversi ambienti sono riportati nella tab. 4, dalla quale si evince che la teoria di Owens-Wendt è in grado di dare conto del fatto che in presenza di un liquido, o anche semplicemente di umidità, molti legami adesivi cedono.

Nel corso degli anni sono state sollevate varie obiezioni al modello termodinamico, ma la sua semplicità e i numerosi ambiti di applicazione lo rendono molto apprezzato da chi lavora nel campo dell'adesione. Le principali critiche riguardano sia l'isteresi, che si osserva nella misurazione degli angoli di contatto e che indica che i processi descritti dal modello non sono perfettamente reversibili, sia l'uso della media geometrica nella [6]. Riguardo a quest'ultimo aspetto menzioniamo alcune tra le osservazioni più rilevanti: secondo Souheng Wu, la media geometrica dovrebbe essere sostituita dalla media armonica; Fowkes ha messo in evidenza come l'uso della media geometrica non sia corretto per le interazioni acido-base di Lewis, legame a idrogeno incluso, che possono essere descritte da un termine aggiuntivo; Carel J. van Oss, Robert J. Good e Manoi K. Chaudury hanno proposto invece di estendere il metodo della media geometrica anche alle interazioni acido-base di Lewis, introducendo due nuove componenti della tensione superficiale, γ⁺ e γ⁻.

Aspetti reologici

Una descrizione degli aspetti reologici è d'importanza fondamentale nella scienza dell'adesione, perché consente di mettere in relazione l'adesione cosiddetta pratica con quella detta fondamentale. Il modello di più frequente uso, proposto da Alan N. Gent e Jacques Schultz, afferma che l'energia di frattura G_a è il prodotto del lavoro termodinamico di adesione W_A per una funzione di perdita f, che dipende dalla velocità v di propagazione della frattura e dalla temperatura T:

[9] G_a = W_Af (v,T).

La f tiene conto dell'energia dissipata per via viscoelastica o plastica dai materiali che formano il giunto e costituisce il principale contributo a G_a. D'altra parte, nella [9] compare come fattore moltiplicativo il lavoro termodinamico di adesione, che svolge quindi un ruolo determinante nello stabilire se tra due materiali vi sia o meno adesione; una riprova di tale ruolo è data dall'ultima colonna della tab. 4, che mostra come non vi sia adesione per W_A〈0. La [9] è spesso scritta nella forma

[10] G_a = G₀Φ(v,T)

fig. 6

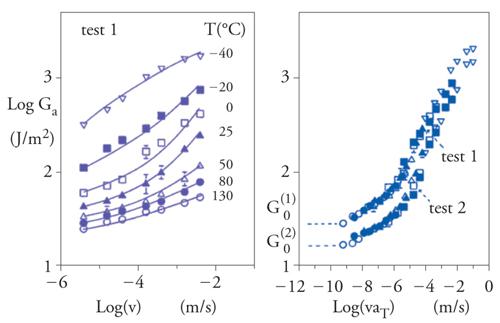
dove G₀ è il valore limite a basse velocità e alte temperature, altrimenti noto come energia di frattura intrinseca: rappresenta l'adesione misurata in condizioni vicine all'equilibrio termodinamico, qualora la dissipazione viscoelastica sia trascurabile. Spesso G₀ è maggiore di W_A, perché all'interfaccia di un giunto intervengono fenomeni irreversibili. Per esempio, il valore teorico di G₀ per l'adesione tra polimeri vetrosi è dell'ordine di 1 J/m², a causa dell'energia dissipata per attrito durante l'estrazione delle catene polimeriche che attraversano l'interfaccia (chain pull-out). Nel caso degli elastomeri reticolati, invece, per separare le due superfici di un giunto quelle stesse catene devono essere rotte (chain scission); per di più, per scindere anche un singolo legame chimico lungo una catena polimerica bisogna prima deformare fino al punto di rottura tutti i legami compresi tra due ponti di reticolazione. Per questo, Alain Carré e Schultz hanno proposto di scrivere G₀=W_Ag(M_c), dove g è una funzione di dissipazione molecolare che dipende dal peso molecolare M_c tra i ponti di reticolazione, e hanno verificato la loro teoria su giunti di gomme e di alluminio. I valori tipici di G₀ variano tra 10 e 100 J/m² se i giunti coinvolgono elastomeri, nel qual caso la funzione Φ(v,T) rispetta l'equivalenza tempo-temperatura di Williams, Landel e Ferry (WLF) e può essere scritta Φ(v,T)=Φ(va_T), dove log[a_T]=17,5(T−T_g)/(52+T−T_g) e T_g è la temperatura di transizione vetrosa (fig. 6): è così confermato che il contributo principale a Φ proviene dalla dissipazione viscoelastica.

Ruolo del legame chimico

tab. 1

fig. 7

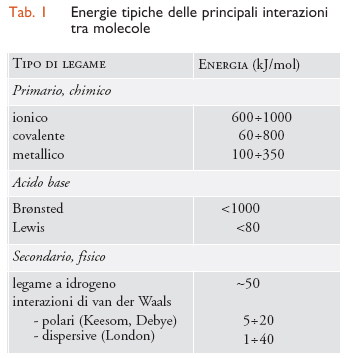
Come risulta evidente dalla tab. 1, i legami chimici, se presenti, possono aumentare considerevolmente l'adesione rispetto ai valori che si avrebbero per effetto dei soli legami fisici. Verificare sperimentalmente la presenza di legami chimici all'interfaccia di un giunto adesivo, tuttavia, è un compito assai difficile, fatta eccezione per casi particolari come l'adesione tra ottone e gomma vulcanizzata con zolfo, dovuta alla formazione di legami polisolfurici, e le interfacce metallo-polimero, in cui spesso si formano legami chimici a seguito del trasferimento di elettroni dal primo al secondo. I legami chimici sono anche alla base del funzionamento degli agenti di accoppiamento (coupling agents), molecole capaci di reagire sia con l'adesivo sia con il substrato, molto usate per migliorare l'adesione di un giunto, soprattutto dal punto di vista della resistenza all'umidità. Gli agenti di accoppiamento più diffusi sono i silani, che all'interfaccia tra vetro e polimeri formano legami covalenti con entrambi i materiali. Per migliorare l'adesione all'interfaccia tra polimeri immiscibili si possono usare opportuni copolimeri, purché formati da due blocchi, ognuno dei quali miscibile con un polimero diverso (fig. 7): ogni blocco si dissolve in un materiale diverso e porta alla formazione di grovigli (entanglements) talmente difficili da districare che, per rompere il giunto, è necessario spezzare i legami C‒C del copolimero. Perché l'interfaccia sia effettivamente rinforzata, tanto i blocchi del copolimero quanto i due polimeri devono avere pesi molecolari sufficientemente alti, maggiori cioè del proprio peso molecolare M_e tra i grovigli: in caso contrario, questi ultimi possono essere facilmente disaggrovigliati. Esperimenti condotti da Gent e A. Ahagon sui silani hanno evidenziato che l'effetto di questi agenti di accoppiamento è quello di far aumentare l'energia di frattura intrinseca G₀, proporzionale alla densità superficiale Σ di legami che attraversano l'interfaccia del giunto; Hugh Brown ha invece studiato l'effetto di copolimeri a blocchi all'interfaccia tra polimeri vetrosi, mostrando che a basse densità superficiali l'energia di frattura G_a è proporzionale a Σ, mentre a densità più elevate G_a∝Σ ² e si osservano le tipiche 'screpolature' (crazes) intorno alla frattura.

fig. 8

Riguardo alla resistenza delle saldature tra polimeri diversi o di un polimero con se stesso (autoesione), essa è dovuta alla presenza di catene polimeriche e quindi legami C‒C, che attraversano l'interfaccia a seguito dell'interdiffusione tra aderendo e substrato (fig. 8). Tale diffusione avviene a due condizioni, che i due polimeri siano mutualmente solubili e che le catene siano sufficientemente mobili: la prima è soddisfatta per alcune coppie di polimeri parzialmente miscibili e, ovviamente, nel caso dell'autoesione; la seconda, per ciascuno dei materiali, al di sopra della temperatura di transizione vetrosa T_g. L'aspetto scientifico più rilevante di questo fenomeno è legato alla dinamica delle catene polimeriche, che determina la dipendenza dell'energia di frattura dal peso molecolare dei polimeri, dallo spessore dell'interfase e da alcuni parametri del processo di saldatura, quali temperatura e tempo t_c di contatto tra i due materiali. La migliore descrizione del moto delle catene in polimeri fusi è quella offerta dalla teoria della reptazione (reptation) elaborata da Pierre-Gilles de Gennes, Masas Doi e Sir Samuel F. Edwards, e William W. Greassley, che, in accordo con gli esperimenti, prevede che valga la relazione G_a∝t_c^1/2.

fig. 9

Nel concludere, ricordiamo che sono state elaborate teorie dell'adesione che, pur meno rilevanti dal punto di vista scientifico rispetto a quelle sopra esposte, individuano validi criteri per migliorare l'adesione tra due sostanze. Tra esse citiamo quella dell'incastro meccanico (mechanical interlocking), secondo cui l'adesione è conseguenza del fatto che l'adesivo si incastra nei pori e nelle asperità del substrato, come accade per il legno, la carta e i tessuti; questa circostanza non è sufficiente a spiegare un fenomeno tanto complesso, ma mette in evidenza il fatto che aumentando la porosità o la rugosità di un materiale si può migliorare la sua adesione. Un altro esempio è costituito dalla teoria dello strato interfacciale debole (weak boundary layer), secondo cui la rottura di un giunto avviene sempre all'interno di un'interfase che si crea tra adesivo e substrato, a causa della presenza di aria, impurezze o prodotti di reazioni chimiche (fig. 9): pur non valendo in generale, le va riconosciuto il merito di aver messo in risalto l'importanza dell'interfase, e in particolare la necessità di eliminarla o rinforzarla al fine di ottenere una buona adesione.

Bibliografia

Comyn 2005: Comyn, John, Theory of adhesion, in: Handbook of adhesives and sealants, edited by Philippe Cognard, II, Amsterdam-London, Elsevier, 2005.

Israelachvili 1985: Israelachvili, Jacob N., Intermolecular and surface forces, London, Academic Press, 1985.

Kinloch 1987: Kinloch, Anthony J., Adhesion and adhesives. Science and technology, Berlin, Springer Netherland, 1987.

Lee 1991: Fundamentals of adhesion, edited by Lieng-Huang Lee, Berlin, Springer, 1991.

Packham 2005: Handbook of adhesion, 2. ed., edited by David E. Packham, Chichester, Wiley, 2005.

Pizzi, Mittal 2003: Handbook of adhesive technology, 2. ed., edited by Antonio Pizzi, Kashmiri Mittal, New York, Dekker, 2003.

Wu 1982: Wu, Souheng, Polymer interface and adhesion, New York, Dekker, 1982.