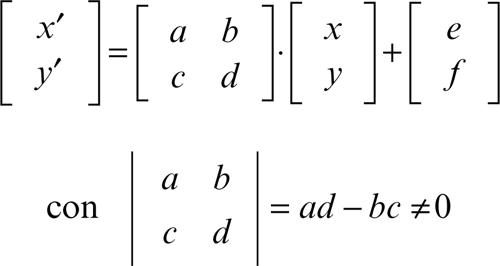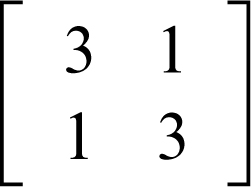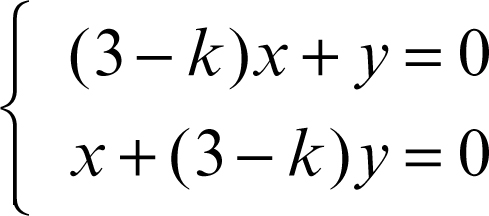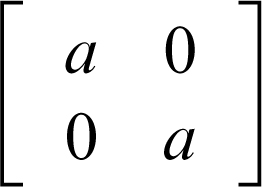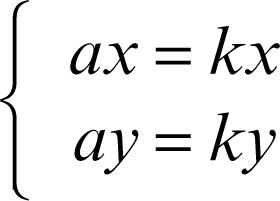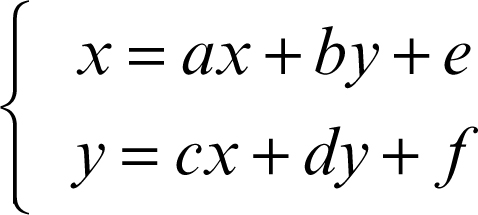affinità

affinita

affinità o trasformazione affine, in geometria, corrispondenza biunivoca tra spazi che ha come invarianti l’allineamento dei punti (è quindi una collineazione poiché muta rette in rette) e il parallelismo. Da ciò segue che un’affinità muta parallelogrammi in parallelogrammi e parallelepipedi in parallelepipedi, ma, in generale, non mantiene né la forma né le dimensioni di una figura. Altro invariante caratteristico di una affinità, dipendente dai precedenti, è il rapporto semplice di tre punti allineati, da cui segue che se M è il punto medio di un segmento AB, il suo corrispondente M′ nell’affinità è ancora il punto medio del segmento corrispondente A′B′. L’insieme delle affinità di uno spazio in sé costituisce un gruppo rispetto all’operazione di composizione di corrispondenze e ciò permette di definire lo spazio affine come quello spazio caratterizzato dal suo gruppo di trasformazioni associato.

Affinità come modello matematico di un fenomeno fisico

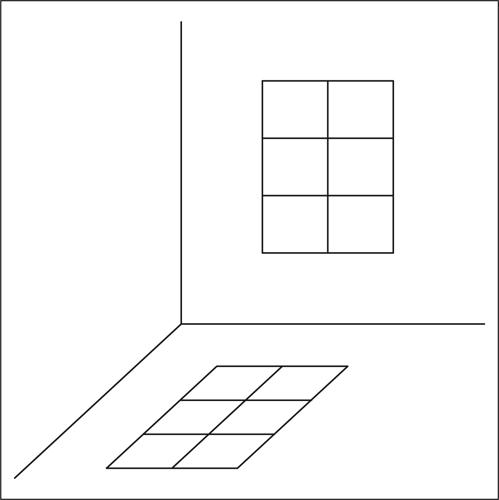
Nell’ordinario spazio tridimensionale, un esempio di trasformazione affine è fornito dalla corrispondenza prodotta dalla luce solare tra i punti di un reticolato piano, per esempio quello di una

, e quelli della sua ombra sul pavimento. Infatti, in tale corrispondenza, che è ottenuta per proiezione parallela dei raggi solari, ai segmenti paralleli degli stipiti e delle segmentazioni lignee dei vetri della finestra corrispondono, nell’ombra sul pavimento, segmenti ancora paralleli. In una tale trasformazione, a una circonferenza corrisponde, in generale, un’ellisse (si pensi per esempio all’ombra di un cartello stradale di forma circolare), mentre parabole si trasformano in parabole e iperboli in iperboli.

Affinità nel piano

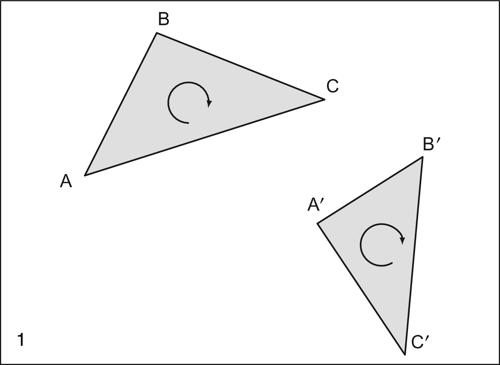
È la trasformazione affine di un piano in sé stesso. Essa risulta completamente individuata quando nel piano sono assegnati tre punti A, B, C non allineati e i loro trasformati A′, B′, C′ anch’essi non allineati, ma può mantenere o meno l’orientamento (se orario o antiorario) nel piano di tali punti. Si distingue, quindi, tra affinità che mantengono l’orientamento nel piano e affinità che lo invertono. Nel primo caso, l’affinità è detta

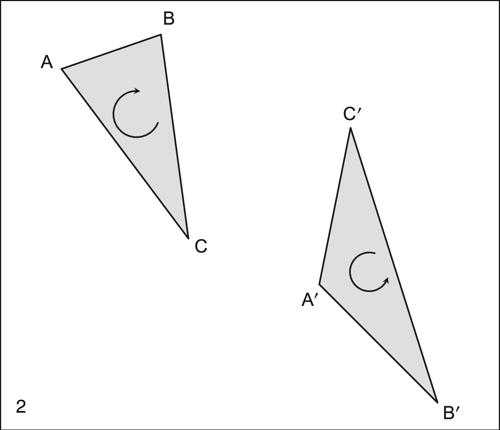
, nel secondo è detta

(o inversa).

In un’affinità del piano, le aree delle figure corrispondenti (che si dicono dunque affini) hanno rapporto costante e, a seconda che l’affinità sia diretta o invertente, tale costante non nulla (detta rapporto o costante di affinità) è rispettivamente positiva o negativa.

Descrizione analitica di un’affinità

Da un punto di vista analitico, una trasformazione affine è una trasformazione di uno spazio vettoriale V in sé, definita da una relazione del tipo S(x) = T(x) + v, dove v è un elemento fissato di V e T è una trasformazione lineare invertibile, rappresentata quindi da una matrice quadrata non singolare, cioè a determinante non nullo.

In uno spazio euclideo n-dimensionale, un’affinità è pertanto descritta da equazioni del tipo

in cui A è una matrice n × n con determinante non nullo. Tale matrice è detta matrice dell’affinità.

Descrizione analitica delle affinità nel piano

Utilizzando il simbolismo matriciale, le equazioni di un’affinità piana si scrivono nel modo che segue:

Nel caso in cui risulta e = ƒ = 0, l’affinità associata ha come punto unito l’origine. Un’affinità piana è data pertanto dalla composizione di un’affinità con punto unito l’origine con una traslazione di vettore di componenti (e, ƒ). Il determinante (ad − bc) della matrice dei coefficienti è il rapporto di affinità. In particolare, se risulta ad − bc = ±1 si ha un’affinità equivalente, così denominata perché mantiene le aree. Casi particolari di affinità equivalenti sono le isometrie.

Caratterizzazione delle affinità del piano sulla base degli elementi uniti

I punti e le rette che in una trasformazione di un piano in sé corrispondono a sé stessi sono detti, rispettivamente, punti uniti e rette unite della trasformazione. Le rette unite dell’affinità definiscono le direzioni che restano immutate nella trasformazione: sono le direzioni invarianti dell’affinità e il loro numero caratterizza diversi tipi di affinità.

Poiché non è restrittivo porre nelle equazioni di un’affinità piana, e = ƒ = 0, giacché l’azione della trasformazione risulta pienamente descritta, a meno di una traslazione, dalla matrice dei coefficienti, per determinare le direzioni invarianti dell’affinità si cercano i valori di k per i quali il sistema

abbia soluzioni diverse dalla coppia (0, 0), cioè risulti indeterminato. Ciò accade solo se il determinante della matrice dei coefficienti di tale sistema è nullo e cioè soltanto se l’equazione

vale a dire

ha soluzioni reali. Tale equazione è detta equazione caratteristica dell’affinità. Ciascun valore di k non nullo che risolve l’equazione caratteristica prende il nome di rapporto di stiramento (o autovalore) e individua una direzione invariante (o autovettore).

Per esempio, per trovare le direzioni invarianti dell’affinità piana la cui matrice dei coefficienti è

occorre considerare il sistema

e quindi risolvere l’equazione caratteristica k² − 6k + 8 = 0, che ha soluzioni k₁ = 2 e k₂ = 4. Sostituendo tali valori nel sistema, si ottengono le equazioni delle due rette unite: rispettivamente, x + y = 0, cioè y = −x, e x − y = 0, cioè y = x. Ciò significa che tale affinità fa corrispondere a ogni punto P appartenente alla retta y = −x un punto P′ sulla medesima retta tale che OP′ = 2OP (perché k₁ = 2 è il rapporto di stiramento) e a ogni retta parallela a y = −x fa corrispondere una retta anch’essa parallela a y = −x (perché m₁ = −1 è la direzione invariante). Analogamente per k₂ e m₂. Si ottengono così due direzioni invarianti dell’affinità.

A seconda del numero delle soluzioni reali non nulle dell’equazione caratteristica, un’affinità del piano può quindi avere due distinte direzioni invarianti, una sola direzione invariante, nessuna direzione invariante. Si osservi tuttavia che un’affinità del piano può anche avere infinite direzioni invarianti: è questo il caso di un’affinità la cui matrice dei coefficienti sia del tipo

con a ≠ 0. In tale caso, infatti, l’equazione caratteristica è (k − a)² = 0, le cui due soluzioni coincidenti sono k = a. Sostituendo tali valori nel sistema

si ottengono perciò le identità ax = ax e ay = ay che, per a ≠ 0, sono sempre soddisfatte. Tali affinità con infinite direzioni invarianti sono le omotetie. Poiché le similitudini si ottengono dalla composizione di una omotetia con una traslazione, sia le omotetie sia le similitudini sono particolari affinità.

Nel piano affine ampliato con i punti impropri, infine, l’affinità si caratterizza come quella particolare trasformazione proiettiva che ha come retta unita la retta impropria.

Per determinare se un’affinità del piano ha punti uniti si opera in modo analogo a quanto fatto per determinare le direzioni invarianti. Si considera cioè il sistema che la definisce, ponendo questa volta x′ = x e y′ = y:

Risultano tre possibilità: il sistema non ammette soluzioni, e allora l’affinità non ha alcun punto unito; il sistema ammette una soluzione, e allora l’affinità ha un solo punto unito ed è detta affinità centrale; il sistema ammette infinite soluzioni, che risultano essere tutti i punti di una retta: in quest’ultimo caso, l’affinità ha perciò una retta unita che inoltre ha la caratteristica di corrispondere a sé stessa punto per punto ed è perciò una retta fissa, detta asse dell’affinità. L’affinità è allora detta affinità omologica (per la sua particolare costruzione grafica, si rimanda a tale lemma); una qualsiasi affinità può essere ottenuta componendo un’affinità omologica con una similitudine (o viceversa).