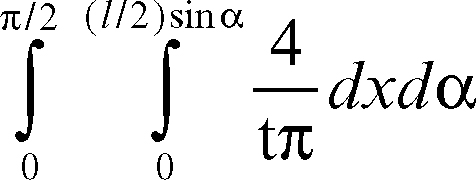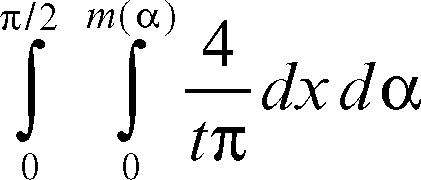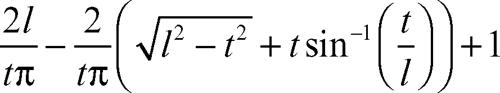Buffon, ago di
Buffon, ago di
Buffon, ago di espressione con cui si indica un problema di probabilità posto dal conte di Buffon nel xviii secolo, così formulabile: se un ago cade su un pavimento in parquet a strisce, tutte della stessa larghezza, qual è la probabilità che l’ago cada su una linea tra due strisce? Il problema rimanda alla delicata questione dell’estensione a variabili casuali continue di strumenti concettuali nati per variabili discrete. Esso, infatti, si risolve ricorrendo all’uso di strumenti di calcolo integrale.
Indicate con t la larghezza di ogni striscia, con l la lunghezza dell’ago, con x la distanza del centro dell’ago dalla linea più vicina e con α l’ampiezza dell’angolo acuto tra ago e linee, si ha:
a) se t ≤ l allora la probabilità che l’ago attraversi una linea risulta essere
che è uguale a 2l /tπ.
Da questo risultato si può ottenere per n aghi lanciati la probabilità che p incidano le linee:
che permette di ricavare un valore approssimato di
con un procedimento del metodo → Montecarlo;
b) se t < l allora la probabilità risulta essere
dove m(α) indica il minimo tra
Risolvendo l’integrale si ha che la probabilità per t < l è:
