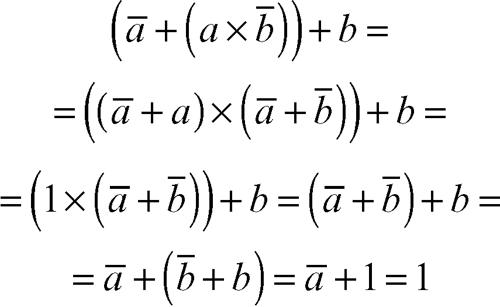Boole, algebra di
Boole, algebra di
Boole, algebra di particolare struttura algebrica, introdotta originariamente da G. Boole. Permette di effettuare un calcolo algebrico che ha come oggetti non i numeri, ma i valori di verità di enunciati. Poiché questi ultimi, nella logica classica, possono assumere soltanto due valori («vero», indicato anche con 1, oppure «falso», indicato anche con 0) l’algebra di Boole nasce come algebra binaria e le sue variabili, dette variabili booleane, possono assumere solo i due valori 0 e 1. Fra tali variabili sono definite le seguenti operazioni:
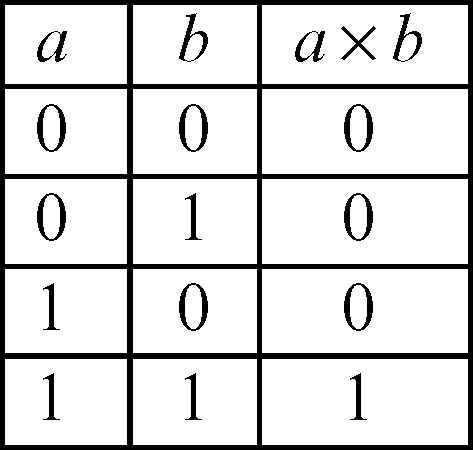
a) prodotto logico detto anche and: è un’operazione binaria che si indica con il simbolo × e corrisponde al connettivo logico della congiunzione «e»; associa a ogni coppia di elementi a e b l’elemento a × b il cui valore è definito dalla seguente tabella:
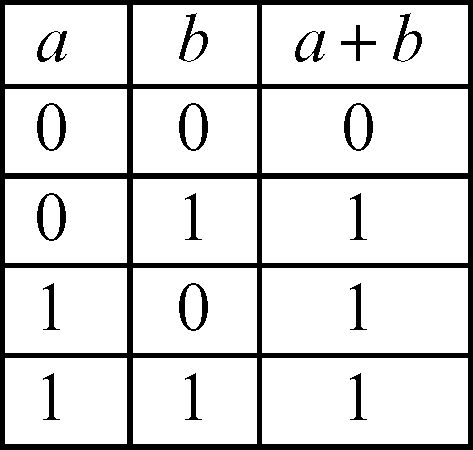
b) somma logica detta anche or: è un’operazione binaria che si indica con il simbolo + e corrisponde al connettivo logico della disgiunzione «o»; associa a ogni coppia di elementi a e b l’elemento a + b il cui valore è definito dalla seguente tabella:
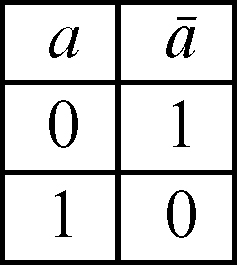
c) complemento detto anche not: è un’operazione unaria che corrisponde al connettivo logico della negazione «non»; associa a ogni elemento a l’elemento ā il cui valore è definito dalla seguente tabella:
Le operazioni definite soddisfano le seguenti proprietà:
• commutativa
• associativa
• distributiva
• esistenza dell’elemento neutro
• esistenza di un elemento assorbente
• esistenza del complementare
• idempotenza
• leggi di De Morgan
Attraverso tali proprietà, per molti aspetti differenti da quelle relative all’algebra ordinaria, è possibile un calcolo che traduce in termini algebrici il calcolo delle proposizioni, interpretando le variabili come enunciati di un linguaggio logico, i valori 0 e 1 da esse assunti come valori di verità falso o vero e le operazioni come connettivi. In questo modo una proposizione logica può essere studiata avvalendosi delle tecniche del calcolo algebrico. Per esempio, per conoscere il valore di verità dell’enunciato
senza utilizzare le tavole di verità, si può tradurre l’enunciato nei termini dell’algebra di Boole binaria, ottenendo l’espressione
alla quale si possono applicare le regole di calcolo precedenti. Lo sviluppo del calcolo è il seguente:
Il valore dell’espressione precedente è quindi sempre 1 e l’enunciato ha sempre il valore di verità «vero» indipendentemente dai valori di verità delle lettere enunciative che lo compongono (si parla in questo caso di tautologia).
L’algebra di Boole può essere applicata, oltre che alla logica, anche alla teoria degli insiemi e ai → circuiti logici. Alle operazioni di unione e intersezione fra insiemi corrispondono rispettivamente le operazioni di somma e prodotto logico fra variabili, mentre al complemento di una variabile corrisponde l’insieme complementare. I due valori 0 e 1 denotano rispettivamente l’insieme vuoto e l’insieme universo. Con questi presupposti si può verificare che valgono tutte le proprietà precedenti applicate agli insiemi, in particolare si possono riscrivere le leggi di De Morgan per gli insiemi indicando con C(X) il complementare dell’insieme X:
Da un altro punto di vista, un’algebra di Boole può essere anche essere definita come un reticolo distributivo complementato, cioè come un insieme A dotato di un ordinamento parziale, indicato con ≤, tale che per ogni coppia di elementi x e y esiste il loro estremo superiore x ∨ y e il loro estremo inferiore x ∧ y. In A esiste un massimo indicato con 1 e un minimo indicato con 0 e il reticolo è detto complementato, perché per ogni elemento di A esiste un complemento, cioè un elemento y tale che si abbia x ∨ y = 1 e x ∧ y {{{1}}} 0, e distributivo perché le due operazioni ∨ e ∧ godono della proprietà distributiva l’una rispetto all’altra.
Più in generale, svincolandosi dalla definizione originaria che si limita a considerare variabili a due soli valori, si definisce algebra di Boole una struttura algebrica formata da un insieme, che contenga almeno due elementi, indicati con 0 e 1, due operazioni binarie, indicate con × e +, una operazione unaria, detta negazione o complemento, indicata con una linea soprassegnata, in cui valgono le proprietà precedentemente elencate. Le algebre di Boole sono molto importanti nello studio della logica classica: infatti l’algebra di → Lindenbaum di ogni sistema assiomatico basato sulla logica classica risulta essere un’algebra di Boole.