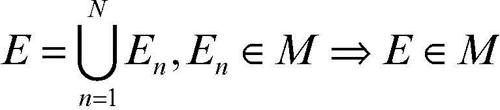algebra di insiemi

algebra di insiemi

algebra di insiemi famiglia M di sottoinsiemi di un insieme qualsiasi Ω che verifica le seguenti condizioni:

a) Ω ∈ M (l’insieme stesso appartiene alla famiglia);

b) E ∈ M ⇒ E^C ∈ M (se un sottoinsieme appartiene alla famiglia gli appartiene anche il suo complementare);

c)

(l’unione finita di insiemi della famiglia appartiene alla famiglia).

Da a) e b) si ricava che anche l’insieme vuoto ∅ appartiene alla famiglia.

La famiglia M, detta algebra o anche algebra su Ω, è quindi non vuota, chiusa per complementazione e per unione finita. Risulta anche chiusa per intersezione finita. Infatti

e quest’ultima espressione indica un sottoinsieme che appartiene a M per le proprietà b) e c). Se la condizione c) vale non solo per una unione finita di sottoinsiemi, ma anche per unioni numerabili, si parla di σ-algebra (sigma algebra) o anche di tribù su Ω.

La più piccola algebra che contiene una famiglia F di insiemi si dice generata da tale famiglia F ed è generalmente contrassegnata con un asterisco: M* (→ Borel, insiemi di).

Le algebre di insiemi sono utilizzate in teoria della probabilità (più in generale in teoria della misura), in cui servono a formalizzare la nozione di evento, e in analisi funzionale: esse sono introdotte perché, in molti casi, l’insieme delle parti è una famiglia molto grande e si ricorre quindi a un suo indebolimento che ne conservi le principali proprietà.