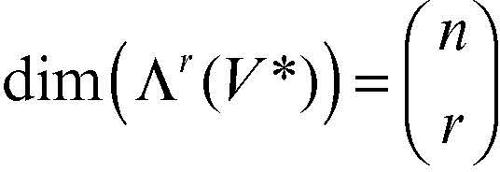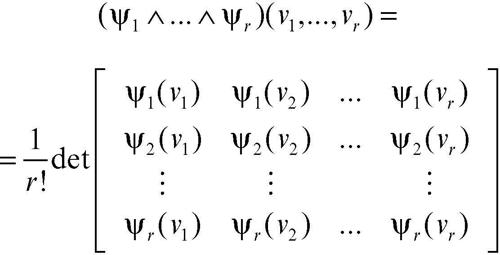algebra esterna

algebra esterna

algebra esterna o algebra di Grassmann, in geometria algebrica o in geometria differenziale, l’algebra esterna di uno spazio vettoriale V* su un campo K è l’algebra associativa unitaria Λ(V*) generata da V* modulo le relazioni {v² = 0, ∀v ∈V*}, vale a dire come il quoziente dell’algebra tensoriale T(V*) rispetto all’ideale I generato dall’insieme {v ⊗v; ∀v ∈V*}, dove con il simbolo ⊗ viene indicato il prodotto tensoriale. Le algebre esterne, che rientrano nell’ambito più generale delle algebre di → Clifford, costituiscono il contesto algebrico più appropriato in cui considerare la nozione di forma differenziale.

In modo più costruttivo, ma sostanzialmente equivalente, si può definire un’algebra esterna a partire da uno spazio vettoriale V* di dimensione n su un campo K (dove K è il campo R dei numeri reali o quello C dei numeri complessi, o più in generale un qualsiasi campo di caratteristica 0) e dal suo spazio duale V**. Si considera il sottospazio vettoriale ΛV*^rV*(V**) ⊆ T(V**) degli r-tensori alterni su V*, cioè dei tensori che:

• costituiscono un’applicazione

• sono r-lineari, sono cioè lineari in ognuna delle loro r-componenti;

• sono alterni, tali cioè che, comunque si scelgano una permutazione σ dell’insieme {1, 2, …, r} e r vettori

v₁, v₂, …, v_r di V*, vale

dove sgn(σ) è il segno di σ.

L’esempio fondamentale di n-tensore alterno è il determinante, visto come applicazione

dove gli n argomenti sono considerati come le colonne di una matrice n × n; ogni altro n-tensore alterno è un multiplo del determinante. Se r > n, allora non esistono r-tensori alterni; gli 1-tensori alterni coincidono invece con le applicazioni lineari: Λ¹(V**) =V**. Si pone infine per definizione Λ⁰(V**) =K. Sia Λ(V**) il sottospazio dell’algebra tensoriale T(V*) somma diretta dei sottospazi ΛV*^rV*(V**) al variare di r tra 0 e n:

Il prodotto tensoriale di tensori alterni non è alterno; tuttavia è possibile definire a partire dal prodotto tensoriale un prodotto (indicato con il simbolo ∧ e detto prodotto esterno o prodotto wedge) tra tensori alterni come segue. Se φ è un r-tensore, sia Alt(φ) l’r-tensore alterno definito come segue:

dove S_r indica l’insieme delle permutazioni dell’insieme {1, 2, ..., r}, r! è il fattoriale di r e, se σ ∈ S_r, il simbolo φ^σ indica l’r-tensore definito come segue:

Nel caso in cui φ è un tensore alterno, allora Alt(φ) = φ: si ottiene pertanto un’applicazione lineare Alt: T(V**) → Λ(V**) che preserva il grado dei tensori e che è l’identità ristretta al sottospazio dei tensori alterni. Si definisce dunque il prodotto esterno di due tensori alterni ξ e ω (rispettivamente di grado r e di grado s) come l’(r + s)-tensore alterno ξ ∧ ω{{{1}}}Alt(ξ ⊗ ω).

Il prodotto esterno di tensori alterni così definito è associativo e bilineare; inoltre esso è antisimmetrico, nel senso che vale ξ ∧ ω{{{1}}}(−1)V*^rsV*ω ∧ ξ.

Dotato del prodotto esterno, lo spazio vettoriale Λ(V**) acquisisce la struttura di algebra associativa unitaria e, con tale struttura, esso è l’algebra esterna di V**.

Se {φ_1, φ_2, ..., φ_n} è una base di V**, allora una base di Λ(V*) è costituita dai vettori

in particolare si ottiene che, se r ≤ n, la dimensione degli spazi vettoriali ΛV*^rV*(V*) è la seguente:

Una volta che Λ(V*) è dotato della struttura di algebra con il prodotto ∧, il tensore determinante acquisisce un ruolo fondamentale; ogni tensore alterno è infatti esprimibile per mezzo di esso secondo la seguente formula: se ψ₁, ..., ψ_r sono elementi di V* = Λ¹(V*) (con r ≤ n), allora

Poiché il nucleo dell’applicazione Alt coincide con l’ideale I rispetto al quale è stata costruita l’algebra tensoriale quoziente T(V*)/I considerata all’inizio, le due costruzioni producono oggetti isomorfi.