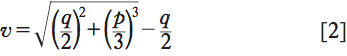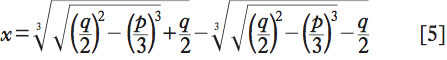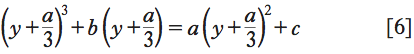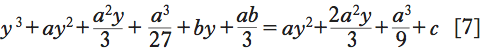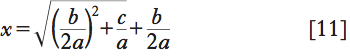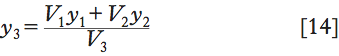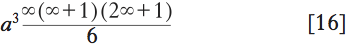Algebra, geometria, indivisibili
Algebra, geometria, indivisibili
Primi progressi nell’algebra
Dopo un periodo di gestazione lungo tre secoli, l’algebra è la prima disciplina in cui nel Cinquecento si registrano sostanziali progressi. Il Medioevo aveva tramandato un’algebra essenzialmente limitata alle equazioni di secondo grado, anche se su questo tronco ereditato dalla matematica araba si erano venute innestando ricerche a volte ingenue, ma in alcuni casi promettenti, riguardanti tipi speciali di equazioni di grado superiore, che in alcuni casi giungevano fino al sesto. Se, infatti, nella maggior parte dei casi le equazioni di ordine superiore erano risolte con procedimenti improntati direttamente da quelle di secondo grado, non di rado era trasparente il tentativo di cercare nella considerazione di casi particolari un algoritmo generale, che potesse adattarsi a tutte le equazioni (Giusti 1991). Secondo la ricostruzione storica di Ettore Bortolotti (L’algebra nella scuola matematica bolognese del secolo XVI, «Periodico di matematiche», s. IV, 1925, 3, pp. 147-84), è proprio da ricerche di questo tipo che emerge il primo risultato originale della matematica moderna: l’algoritmo risolutivo dell’equazione di terzo grado.
La soluzione fu trovata agli inizi del Cinquecento dal matematico Scipione Dal Ferro (1465-1526), professore all’Università di Bologna. Di lui non ci sono pervenuti scritti, ma si sa che annotava le sue scoperte in un quadernetto che il suo genero e successore Annibale Della Nave (1500-1558) conservava ancora nel 1542, e che giocò un ruolo non secondario nella storia delle equazioni algebriche.
La scoperta di Del Ferro non rimase comunque sconosciuta. Essa venne comunicata a due suoi ex allievi, Pompeo Bolognetti (professore a Bologna nella seconda metà del Cinquecento), che la inserì in una sua opera rimasta manoscritta (Regole principali dell’arte maggiore, detta regola della cosa, over d’algibra), e Antonio Maria Fior (fine 15° sec.-dopo il 1540), che se ne servì per sfidare alcuni matematici del suo tempo.
Fu proprio in occasione di una di queste disfide matematiche che la notizia dell’esistenza di una possibile soluzione venne all’orecchio di Niccolò Fontana detto il Tartaglia, che la trovò per conto suo nel 1535. La storia della scoperta è narrata dallo stesso Tartaglia in Quesiti et inventioni diverse (1546). Fior aveva proposto a Tartaglia trenta quesiti, tutti riconducibili al «capitolo di cosa e cubo uguali a numero», cioè, in linguaggio moderno, all’equazione x3+px=q, vantandosi di aver trovato una regola generale per quella equazione. In principio Tartaglia non credeva a tale vanteria,
perché lui [Fior] non haveva scientia, ma solamente gran pratica, e per la pura pratica io comprendeva chel non era atto né sofficiente a poter haver ritrovata tal regola per sé medesimo. Ma lui per farme credere che havesse tal passo, e che dovesse temere di lui, anchor che non havesse theorica, se avantava che già trenta anni tal secreto gli era stato mostrato da un gran mathematico, il che mi fece dubitar, che’l fusse il vero, e per questo io posi ogni mio studio, cura ed arte per ritrovar regola a tal capitolo, e così per mia bona sorte […] la ritrovai (Quesiti et inventioni diverse, cit., ed. 1554, f. 106v).
Grazie a questa scoperta, Tartaglia riuscì a vincere la disputa con Fior, che da parte sua non riuscì a risolvere nessuno dei quesiti propostigli dall’avversario.
Della vicenda fu informato Girolamo Cardano, che a quel tempo stava redigendo la prima delle sue opere matematiche, la Practica arithmetice et mensurandi singularis (1539). Con un risultato così importante la sua opera sarebbe stata enormemente valorizzata, e Cardano fece subito dei passi in questa direzione, incaricando un libraio di sua fiducia, tale Zuanantonio di Bassano, di sondare le intenzioni di Tartaglia. Il libraio scrisse a quest’ultimo il 2 gennaio 1539:
Messer Nicolò, el me ha drizzato da voi un huomo da bene Medico da Millano, chiamato misser Hieronimo Cardano, el quale è un grandissimo Mathematico, e legge publicamente Euclide lì in Millano, e al presente fa stampare una sua opera in la pratica di Arithmetica e geometria e in Algebra che sarà una bella cosa. Et perché egli ha inteso voi esser stato in una disputa con maestro Antoniomaria Fiore, […] et sua eccellentia ha inteso che il detto maestro Antoniomaria vi propose tutti li suoi 30 che vi conducevano in Algebra in un capitolo di cosa e cubo equal a numero. E che voi trovasti regola generale a tal capitolo […]. Et per tanto sua eccellentia vi prega che voi gli vogliati mandare di gratia tal regola da voi trovata, e s’el vi pare lui la darà fora in la presente sua opera sotto vostro nome, e se anchor el non vi pare che lui la dia fora, la tenerà secreta (in Quesiti et inventioni diverse, cit., ed. 1554, f. 113r).
Il prevedibile rifiuto di Tartaglia non scoraggiò Cardano che, nel febbraio 1539, intervenne di persona reiterando la richiesta e facendo balenare la possibilità di introdurre Tartaglia presso il governatore di Milano, Alfonso d’Avalos marchese di Pescara e del Vasto. Com’è noto, la vicenda si concluse con la trasmissione, sotto vincolo di segreto, dell’algoritmo risolutivo, comunicato sotto forma di «uno capitolo in rima, perché se io non havesse usato questa cautella spesso me saria uscito di mente» (Quesiti et inventioni diverse, cit., ed. 1554, f. 120v). La regola per risolvere l’equazione x3+px=q è contenuta nelle prime tre terzine:
Quando che ’l cubo con le cose appresso
se agguaglia a qualche numero discreto
trovan dui altri differenti in esso.
Dapoi terrai questo per consueto
che ’l lor produtto sempre sia eguale
al terzo cubo delle cose neto.
El residuo poi suo generale
delli lor lati cubi ben sottratti
varrà la tua cosa principale
(Quesiti et inventioni diverse, cit., ed. 1554, f. 120v).
Tradotta in linguaggio moderno, l’equazione x3+px=q si risolve cercando due numeri u e v tali che u−v=q e uv=(p/3)3. Ciò fatto, la soluzione sarà
I due numeri u e v si trovano facilmente, dato che si conosce la loro differenza q e il loro prodotto (p/3)3; di conseguenza, v sarà soluzione dell’equazione di secondo grado v2+qv=(p/3)3, e quindi
In conclusione:
La seconda parte della poesiola di Tartaglia contiene la regola per la soluzione del «capitolo di cubo uguale a cosa e numero» (in termini moderni x3=px+q, caso che per noi è lo stesso di quello precedente con il solo cambiamento di p in −p, ma che all’epoca era trattato separatamente), la cui soluzione è
Questa formula sarà all’origine di molte ricerche successive.
La Practica arithmetice di Cardano uscì nel 1539 senza nessun riferimento all’equazione di terzo grado. Nel 1542 però, ci racconta Ludovico Ferrari (1522-1565), egli e Cardano, in occasione di un viaggio a Bologna, ebbero modo di vedere il quadernetto con gli scritti di Del Ferro, ancora conservato da Della Nave, che conteneva la soluzione dell’equazione. A questo punto Cardano si sentì sciolto dal giuramento, e nel 1545 pubblicò la soluzione nella sua Artis magnae sive De regulis algebraicis liber unus (più nota come Ars magna). La pubblicazione e la successiva risposta di Tartaglia nei Quesiti dettero origine a una vigorosa polemica, con sei cartelli di sfida e sei risposte, tra Ferrari e Tartaglia, e condussero a una pubblica competizione tra i due, della quale ognuno si ritenne vincitore.
L’Ars magna non conteneva però solo la soluzione di Del Ferro comunicata a Cardano da Tartaglia; vi si trovavano anche importanti progressi nella teoria delle equazioni.
In primo luogo, Cardano fa vedere come l’equazione generale di terzo grado, contenente cioè i termini di tutti i gradi, può essere sempre ricondotta, con un semplice cambiamento dell’incognita, a una delle forme di Tartaglia. Per esempio, l’equazione x3+bx=ax2+c, ponendo x=y+a/3 diventa
e sviluppando le potenze
In quest’ultima equazione i termini in y2 si elidono, lasciando
in cui manca il termine di secondo grado. Una volta risolta la [8] con una delle regole di Tartaglia, la soluzione dell’equazione di partenza si ottiene semplicemente sommando la quantità a/3 (Artis magnae…, cit., 4° vol., ed. 1663, pp. 236-40).
In generale, Cardano mostra come eliminare da una qualsiasi equazione di grado n il termine di grado n−1. Nel caso dell’equazione di quarto grado (n=4) l’eliminazione del termine di terzo grado sarà il primo passo per giungere alla sua soluzione completa, che nell’Ars magna è attribuita a Ferrari (Artis magnae…, cit., 4° vol., ed. 1663, pp. 352-56).
Resta invece aperto il problema del cosiddetto caso irriducibile. La formula risolutiva [5] diventa inefficace quando la quantità
sotto la radice è negativa. Si tratta di un’anomalia reale in quanto, a differenza di quanto accade per le equazioni di secondo grado, le radici di numeri negativi non denotano un caso impossibile, ma appaiono quando l’equazione in esame ha tre radici reali. Le strade che si aprono sono essenzialmente di due tipi: o elaborare metodi per la manipolazione di queste radici, chiamate da Cardano «sofistiche», o cercare di risolvere l’equazione per altre vie, che non coinvolgano radici di numeri negativi. Nell’Ars magna Cardano fa alcuni passi nella prima direzione, non tanto nel caso delle equazioni di terzo grado, quanto nello studio delle equazioni di secondo grado con radici complesse. La seconda strada verrà invece tentata nel De aliza regula liber (1570), senza però giungere a nessun risultato positivo.
Di diverso spessore è il tentativo di Raffaele Bombelli che, nel suo L’algebra, parte maggiore dell’aritmetica (1572), riprende le radici sofistiche di Cardano e delinea un’algebra dei binomi
mostrando come si possa operare con queste quantità. Resta però insoluto il problema dell’estrazione delle radici cubiche, che entrano nella formula risolutiva dell’equazione di terzo grado, e che Bombelli non riesce a risolvere se non in casi particolari e ‘a tentoni’. Il caso irriducibile rimarrà tale.
La scoperta di Diofanto
Verso la metà del Cinquecento, nella Biblioteca Vaticana venne alla luce un codice contenente un trattato di Diofanto di Alessandria (attivo intorno al 250), un matematico greco fino allora praticamente sconosciuto. Si tratta dell’Aritmetica, un’opera in sei libri nella quale si usano metodi algebrici per la soluzione di quelli che poi verranno chiamati problemi diofantei, cioè problemi con un numero di incognite sovrabbondanti ma di cui si accettano solo soluzioni razionali. L’opera di Diofanto venne pubblicata in traduzione latina solo nel 1575, ma la sua influenza si era fatta sentire ancor prima. La scoperta di Diofanto ci viene narrata da Bombelli nell’introduzione all’Algebra:
Essendosi ritrovato un’opera greca di questa disciplina nella libraria di Nostro Signore in Vaticano, composta da un certo Diofante Alessandrino Autor Greco, il quale fu al tempo di Antonino Pio, & havendomela fatta vedere Messer Antonio Maria Pazzi Reggiano, publico lettore delle Matematiche in Roma, e giudicatolo con lui Autore assai intelligente de’ numeri (ancorché non tratti de’ numeri irrationali, ma solo in lui si vede un perfetto ordine di operare) egli, & io, per arricchire il mondo di così fatta opera, ci dessimo a tradurlo, e cinque libri […] tradutti ne abbiamo (L’algebra, parte maggiore dell’aritmetica, 1a ed. integrale a cura di U. Forti, E. Bortolotti, 1966, pp. 8-9).
La traduzione di Bombelli non vide mai la luce, ma la sua presenza è evidente nel corpo dell’Algebra, il cui terzo libro viene completamente rimaneggiato e nell’edizione a stampa è quasi interamente dedicato a problemi diofantei. Da questo momento l’analisi diofantea viene integrata sistematicamente nei più avanzati trattati algebrici, dai quali si separerà solo nel Settecento.
Oltre all’inserimento dell’analisi diofantea e allo studio dell’algebra dei binomi [10] l’opera di Bombelli contiene altre importanti novità. In primo luogo, le conoscenze algebriche sulle equazioni fino al quarto grado vengono integrate in una trattazione omogenea, nella quale non poca parte ha un sistema di notazioni molto più agevole di quelli in uso, soprattutto per quanto riguarda le potenze dell’incognita. Infine, una compenetrazione molto avanzata tra algebra e geometria, specialmente evidente nella parte inedita, che sarebbe stata ritrovata e pubblicata soltanto nel secolo scorso.
Fino a Bombelli la geometria entrava nei testi algebrici nella duplice veste di fonte di problemi e di linguaggio dimostrativo. Sono due funzioni che si trovano agli estremi opposti della scala del rigore. Da una parte, per essere assoggettabili all’algebra le grandezze geometriche devono perdere la loro caratteristica costruttiva e ridursi a pure quantità numeriche; dall’altra, affinché le regole dell’algebra possano giustificarsi formalmente occorre reinterpretare le quantità algebriche in termini di oggetti geometrici e applicare a questi le costruzioni e i teoremi degli Elementi di Euclide. Il primo approccio è comune alla maggior parte dei libri d’abaco; il secondo, che risale ad al-Ḫwārizmī (Abū Ǧa‛far Muḥammad ibn Mūsā al-Ḫwārizmī, 780 ca.-850 ca.), è alla base della dimostrazione degli algoritmi risolutivi delle equazioni algebriche. E siccome la geometria non va al di là delle tre dimensioni, anche l’algebra vedrà limitata la sua portata alle equazioni di terzo grado, e avrà – almeno agli inizi – una scarsa attenzione per quelle di grado superiore.
Con Bombelli l’intersezione tra algebra e geometria acquista un altro elemento. Come nella tradizione abachistica, i problemi geometrici vengono tradotti in termini algebrici e ricondotti alla soluzione di equazioni. Ma mentre i libri d’abaco si arrestavano a questo punto, Bombelli reinterpreta le operazioni aritmetiche e l’estrazione di radice quadrata in termini di costruzioni geometriche con riga e compasso, e quindi si serve dell’algoritmo algebrico come guida per la costruzione geometrica. In questo modo tutti i problemi che danno luogo a equazioni di primo e secondo grado possono essere risolti con riga e compasso seguendo le orme della formula, o meglio dell’algoritmo risolutivo.
Un’occasione perduta: l’algebra letterale
Alla fine del Cinquecento si registra un evento destinato a cambiare completamente la struttura dell’algebra: il francese François Viète (1540-1603) inventa l’algebra letterale.
A partire dal Medioevo e per tutto il Cinquecento si era assistito a un progressivo affinarsi del formalismo algebrico: dagli enunciati completamente verbali del Liber abaci (1202) di Leonardo Fibonacci si era passati via via all’introduzione di una serie di abbreviazioni e di qualche simbolo, che avevano prodotto una successiva contrazione della scrittura, fino a giungere alla cosiddetta algebra sincopata. Al di là dell’ovvia economia di scrittura, questo aveva portato un contributo di qualche rilevanza al linguaggio algebrico, e soprattutto a una maggiore capacità di controllo delle equazioni. Nondimeno, anche quando, come in Bombelli, si era giunti a una completa formalizzazione della scrittura delle incognite e delle loro potenze, non era cambiata la struttura degli enunciati che, nella loro forma sincopata, riguardavano sempre una singola equazione, i cui coefficienti erano invariabilmente dei numeri.
L’innovazione principale di Viète consiste nell’indicare con delle lettere non solo le incognite, ma anche i loro coefficienti in un’equazione. Tra le altre cose, questo consente di trattare direttamente il caso generale, e soprattutto di esprimere la soluzione con una formula invece che con un algoritmo. Per capire meglio la portata dell’innovazione vietea, consideriamo, per es., il «capitolo di potenze uguale a tanti e numero», cioè, in termini moderni, l’equazione di secondo grado ax2=bx+c. Senza la forma letterale dei coefficienti, non è possibile scrivere l’equazione generale, e si dovrà quindi esprimere la soluzione non con una formula ma con un algoritmo. Dice Bombelli:
Havendosi da agguagliare potenze a tanti e numero, partasi il tutto per la quantità delle potenze, poi si pigli il mezzo delli tanti e si quadri, ed il produtto si aggionge al numero, e della somma se ne piglia il lato, & a detto lato si aggionge il mezzo delli Tanti, & la somma è la valuta del Tanto. Come se si haverà da agguagliare 12‿ a 121‿ p. 11. Piglisi il mezzo delli Tanti, ch’è 6, il suo quadrato è 36, che gionto a 11 fa 47, che pigliato il suo lato è R. q. 47, & aggiuntoli il mezzo delli Tanti, fa R. q. 47 p. 6, e questo è la natura del Tanto (L’algebra…, cit., ed. 1966, p. 197).
Il confronto con la soluzione algebrica
mostra immediatamente il vantaggio delle nuove notazioni. Se a ciò si aggiunge l’osservazione che la formula risolutiva non è il risultato finale, ma spesso solo un passo intermedio nella soluzione di un problema complesso, si capirà meglio come l’innovazione di Viète non sia solo un’economia di scrittura, ma una chiave che apre una vasta gamma di possibilità altrimenti precluse.
In Italia ben poco giunse delle idee di Viète, meno ancora venne studiato e assimilato. In effetti, si può affermare che gli studi algebrici terminino con Bombelli; nel secolo successivo non si registreranno che tardi epigoni di un’impostazione ormai obsoleta.
La parte più vivace della matematica italiana del Seicento, in particolare gli scienziati della scuola galileiana, trascurerà completamente gli studi algebrici, anche quando ne avrebbe potuto trarre vantaggio per le proprie ricerche. Così vediamo Bonaventura Cavalieri rammaricarsi della mancata conoscenza dell’algebra letterale, che gli avrebbe permesso di risolvere il problema della quadratura della parabola di terzo e quarto grado, in termini moderni dell’integrazione delle funzioni x3 e x4, per il quale invece aveva dovuto ricorrere a un risultato del francese Pierre de Fermat (1601-1655), comunicatogli da Jean de Beaugrand (1584/1595-1640); «che se fosse stata nota la pratica dell’algebra litterale, come allora non ci avevo badato, et ho visto doppo, levavo tal confusione e finivo anch’io la dimostrazione» (Lettera a Torricelli, in Opere di Evangelista Torricelli, a cura di G. Loria, G. Vassura, 3° vol., 1919, p. 234).
A Cavalieri fa eco Evangelista Torricelli, che in una lettera a Michelangelo Ricci (1619-1682), addirittura si fa vanto di non conoscere i metodi di Viète:
Studiamo il foglio della sineresi, et anastrofe, e la maggior parte da me non era intesa punto perché suppone certo metodo Vieteo a me ignoto, e del resto è difficilissimo di spiegatura come mi riescono per lo più gli Oltramontani. Però io trovai un altro metodo non Vieteo, ma evangelisteo, col quale facilmente et in subito senza linee o difficoltà, con pura geometria, e senza neanche l’odor dell’algebra, mostro la seguente proposta (Opere di Evangelista Torricelli, cit., 3° vol., pp. 299-300).
La ragione principale di questo disinteresse per gli studi algebrici sta senza dubbio nella scarsa rilevanza di questi ultimi nel progetto di ricerca della scuola galileiana, tutto orientato verso la geometria e la filosofia naturale, e permeato da un’esigenza di rigore che solo i procedimenti geometrici potevano soddisfare. Così mentre al di là delle Alpi l’algebra di Viète è il punto di partenza per gli studi di Fermat e per la geometria cartesiana, la scuola italiana resterà ancorata ai metodi della geometria classica, certamente più rigorosi ma di gran lunga meno efficaci.
La nuova geometria algebrica di René Descartes (1596-1650) porrà un confine tra il vecchio e il nuovo, non solo per la potenza dei suoi metodi, ma anche e soprattutto perché cambia radicalmente il campo dell’indagine geometrica. Prima di Descartes la geometria si era interessata essenzialmente a oggetti particolari: si studiava una certa curva, per es. la cicloide o la quadratrice, ricercandone le proprietà e le caratteristiche salienti, come potevano essere la tangente in un suo punto generico o l’area racchiusa. Al contrario, anche se non disdegna di studiare casi singoli, l’oggetto della geometria cartesiana è la curva ‘generica’, espressa mediante un’equazione algebrica in due variabili F(x,y)=0, e il problema diventa quello di trovare dei metodi generali, per esempio per le tangenti, che si applichino a ogni genere di curva (Giusti 1987).
Si apre così un campo di indagine completamente nuovo, i cui sviluppi condurranno nel giro di mezzo secolo all’invenzione del calcolo infinitesimale. Da questo processo imponente, destinato a creare la matematica moderna, i matematici italiani sono praticamente assenti; benché le opere di Descartes, in primo luogo la Géométrie (1637), arrivino abbastanza presto in Italia, la geometria cartesiana resterà praticamente ignorata e di fatto penetrerà solo nel secolo successivo insieme al calcolo infinitesimale (Pepe 1982).
La rinascita della geometria
Durante tutta la prima parte del Cinquecento si assiste a un progressivo processo di assimilazione della matematica classica, che vedrà il suo coronamento alla fine del secolo. Il fattore scatenante è senza dubbio l’invenzione della stampa a caratteri mobili, che imprime un’accelerazione senza precedenti alla diffusione delle conoscenze, sia di quelle del passato finalmente recuperate e rese disponibili agli studiosi, sia di quelle nuove che via via vengono prodotte. Se agli inizi sono soprattutto gli Elementi di Euclide a giungere alla stampa, in edizioni sempre più corrette filologicamente e matematicamente, già prima della fine del secolo vengono pubblicati i maggiori testi della matematica greca classica. Vedono così la luce le Coniche di Apollonio di Perge (1537), le Opere di Archimede (1544), l’Aritmetica di Diofanto (1575), la Collezione matematica di Pappo (1588), oltre a una moltitudine di autori ‘minori’. Alla fine del Cinquecento, si può affermare che quasi tutta la matematica classica pervenuta in Occidente è disponibile in una o più edizioni.
Tra le conseguenze di questa ‘rivoluzione culturale’, due sono particolarmente significative. Da una parte, si forma una comunità di studiosi, uniti da un comune sapere diffuso e condiviso; dall’altra, l’appropriazione della matematica classica spinge i matematici ad affrontare nuovi problemi e a tentare nuove vie. Le prime ricerche riguardano quei risultati, sicuramente ottenuti dagli antichi, che erano però stati perduti nel corso dei secoli. Da una parte, si trattava di ricostituire, con un vero e proprio lavoro di divinazione, opere perdute, sommariamente descritte in altri autori; dall’altra, di completare ed estendere i risultati acquisiti.
Ognuno degli autori citati avrà un’importante influenza sullo sviluppo della matematica, e più in generale della nuova scienza. Si è detto di Diofanto, che già prima della sua pubblicazione a stampa aveva segnato profondamente le opere di Bombelli e di Viète, e la cui analisi conoscerà una grande fioritura nel secolo successivo grazie soprattutto alle ricerche di Fermat. Gli Elementi di Euclide costituiranno il fondamento di ogni sapere matematico, e con la teoria delle proporzioni forniranno il linguaggio di elezione della rivoluzione scientifica. Lo stesso può dirsi delle sezioni coniche di Apollonio, che si ritroveranno a ogni passo nella scienza seicentesca, dalla traiettoria dei proiettili alle orbite dei pianeti. Infine, la raccolta miscellanea di metodi e problemi che costituisce la Collezione matematica di Pappo darà lo spunto a Descartes per la formulazione della nuova geometria analitica. Ma tutto ciò avverrà per lo più nel secolo successivo. Nel Cinquecento, il contributo più importante allo sviluppo della matematica deriverà direttamente dalle opere di Archimede.
Le opere di Archimede occupano un posto a parte nella matematica greca. Esse non hanno il carattere sistematico degli Elementi di Euclide e delle Coniche di Apollonio, non riguardano un solo argomento come l’Aritmetica di Diofanto, né d’altro lato sono una raccolta di problemi e metodi disparati come la Collezione di Pappo. Al contrario, si tratta di un numero piuttosto rilevante di scritti, ognuno dedicato a un tema specifico e tutti a carattere avanzato. Per uno studioso del Cinquecento che avesse assimilato gli Elementi e le Coniche, era naturale rivolgersi ad Archimede per trovare una geometria più avanzata e una fonte di ispirazione per le proprie ricerche.
Il primo a dare alle stampe un’opera di chiara ispirazione archimedea fu l’urbinate Federico Commandino (1509-1575). Umanista matematico e traduttore di gran parte delle opere matematiche greche, arricchite da importanti commenti sia filologici sia matematici, Commandino aveva pubblicato nel 1558 la traduzione latina di una scelta di opere di Archimede, cui aveva aggiunto un secondo volume di commenti. La silloge non comprendeva gli Equiponderanti, che furono pubblicati nel 1588 in una parafrasi da Guidobaldo Dal Monte (1545-1607), allievo di Commandino, né i Galleggianti, che invece usciranno nel 1565, sempre nella traduzione di Commandino. La mancanza di queste due opere non è casuale, perché da una parte gli Equiponderanti riguardavano solo i centri di gravità dei piani – in particolare del triangolo e della parabola – senza affrontare l’analogo problema per le figure solide, e dall’altra i Galleggianti, che all’epoca circolavano in un testo greco largamente lacunoso e che presentavano non pochi problemi di interpretazione, facevano riferimento al centro di gravità del paraboloide di rotazione, e quindi rinviavano a un’opera perduta sui centri di gravità dei solidi.
Il problema viene affrontato da Commandino che, congiuntamente all’edizione dei Galleggianti, pubblica nel 1565 il suo Liber de centro gravitatis solidorum, che nelle intenzioni doveva completare l’opera archimedea sui centri di gravità. In realtà Commandino si limita a seguire pedissequamente il metodo sviluppato da Archimede per le figure piane, anche nella disposizione della materia.
Negli Equiponderanti, Archimede aveva trovato successivamente i centri di gravità del parallelogrammo, del triangolo e della parabola. Procedendo per analogia, Commandino determina il centro di gravità del parallelepipedo, del prisma a base triangolare, dei prismi e del cilindro; prosegue poi con il centro di gravità della piramide a base triangolare, delle piramidi e del cono, per terminare l’opera con la dimostrazione del risultato archimedeo relativo al conoide parabolico, in termini moderni del paraboloide di rotazione.
Anche i metodi di dimostrazione sono derivati senza grandi cambiamenti dall’opera archimedea. Per esempio, la dimostrazione della proposizione VII, secondo la quale il centro di gravità del prisma o cilindro giace nel piano parallelo ed equidistante dalle basi (in breve, il piano mediano), è identica, salvo la figura, a quella della proposizione IX del primo libro degli Equiponderanti.
E quando l’aderenza al testo archimedeo non è sufficiente per condurre a termine la dimostrazione, come avviene nel caso del conoide parabolico, Commandino stenta a produrre un ragionamento concludente, e si affida all’esame di alcuni casi e soprattutto alla conoscenza del risultato.
Di ben altro spessore è l’opera sullo stesso tema di Francesco Maurolico. Diversamente da Commandino, interessato soprattutto al recupero dei testi classici di cui dispone, il progetto di Maurolico prevede una ricostruzione completa del sapere matematico. Già il tedesco Regiomontano (Johann Müller, 1436-1476) aveva elaborato un programma simile, e aveva anche predisposto una tipografia per la stampa del materiale che via via avrebbe prodotto, ma la morte prematura gli aveva impedito di iniziare il suo progetto di restaurazione matematica. Maurolico vivrà abbastanza a lungo da portare a compimento un corpus matematico pressoché completo, ma, tranne che per alcune opere tutto sommato minori, la sua produzione resterà per lo più inedita o sarà pubblicata solo nel secolo successivo, troppo tardi per influire sostanzialmente sul progresso della matematica.
Da quanto egli stesso ci dice, Maurolico affronta il problema dei centri di gravità prima ancora di aver visto gli Equiponderanti, sulla base unicamente di alcuni estratti che ne aveva pubblicato l’umanista piacentino Giorgio Valla (prima metà del 15° sec.-1500) nel suo testo postumo De expetendis et fugiendis rebus (1501). Su questa base egli edifica una costruzione che comprende non soltanto i centri di gravità delle figure piane, ma anche quelli delle figure solide, tra le quali il conoide parabolico, dando in questa maniera la prima dimostrazione completa del risultato enunciato da Archimede.
Nuovi orizzonti: Luca Valerio
Sia Commandino sia Maurolico si muovevano ancora nell’ambito dei metodi della geometria classica, tra i quali primeggiava il cosiddetto metodo apagogico della doppia riduzione all’assurdo. Con il napoletano Luca Valerio (1552 ca.-1618), che pure usa estensivamente le stesse tecniche, assistiamo all’innesto di idee nuove nel tronco della tradizione geometrica.
Valerio (Baldini, Napolitani 1991) fu un personaggio complesso e per molti versi contraddittorio. Entrato giovane nella Compagnia di Gesù, ne uscì poco dopo senza aver preso gli ordini, ma mantenne sempre un rapporto con gli ambienti gesuitici, e in particolare con lo studioso tedesco Cristoforo Clavio (Christopher Clau, o Klau, o Schlüssel, 1537-1612). All’uscita dalla compagnia entrò al servizio dei Colonna, alla cui protezione dovette la nomina a correttore di lingua greca presso la Biblioteca vaticana, un posto che mantenne solo per poco più di un anno. Come accompagnatore di Camillo Colonna soggiornò a Pisa, dove ebbe occasione di conoscere Galilei. All’inizio del Seicento venne nominato lettore di greco allo Studium Urbis, e poco dopo assunse la lettura di matematica. Eletto all’Accademia dei Lincei nel 1612, ne uscì nel 1616 a causa del sostegno di quest’ultima alla teoria eliocentrica.
La fama di Valerio è legata soprattutto al suo De centro gravitatis solidorum (1604), un’opera che, come dice il titolo, affronta ancora una volta i problemi trattati da Commandino e da Maurolico, anche se dell’opera di quest’ultimo probabilmente Valerio non aveva notizia. Nei tre libri che la compongono, Valerio ottiene vari importanti risultati, tra i quali spicca il centro di gravità del conoide iperbolico, in termini moderni l’iperboloide di rivoluzione, un risultato anch’esso noto ad Archimede, ma non a Valerio, dato che era esposto nel Metodo, uno scritto archimedeo che sarà ritrovato e pubblicato solo all’inizio del Novecento.
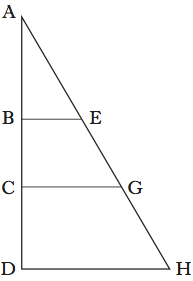
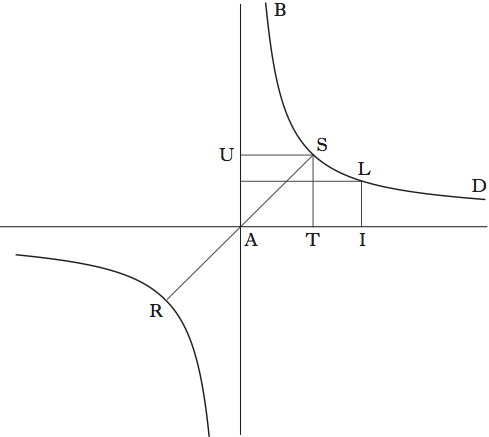
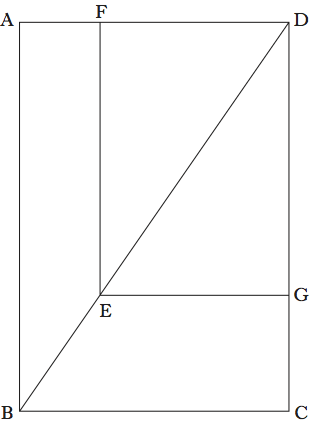
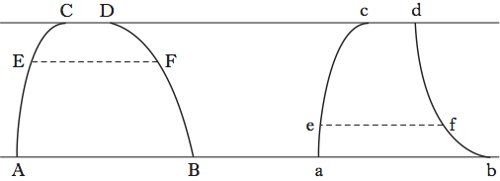
L’idea di Valerio è di confrontare il conoide iperbolico AOB con un conoide parabolico COD e un cono EOF presi insieme (fig. 1).
Per dare un’idea del procedimento, utilizziamo un formalismo algebrico e scriviamo le equazioni dell’iperbole AOB, della parabola COD e del cono EOF, rispettivamente:
Se ora fissiamo un’altezza generica y=GN e poniamo x1=GH, x2=GL e x3=GM, avremo
Moltiplicando tutto per π, avremo allora che l’area del cerchio di raggio x3=GM, sezione del conoide iperbolico con un piano orizzontale, sarà uguale alla somma delle aree dei cerchi di raggi x1=GH e x2=GL, sezioni rispettivamente del conoide parabolico e del cono. Questo avviene qualunque sia l’altezza y alla quale si tagliano le tre figure. Partendo da questo risultato, Valerio dimostra che il centro di gravità del conoide iperbolico coincide con quello della figura composta dal conoide parabolico e dal cono. Poiché i centri di gravità di queste due figure, come pure i loro volumi, sono noti (e Valerio li aveva calcolati in precedenza), sarà possibile trovare anche il centro di gravità del conoide iperbolico. In effetti, detti y1, y2, y3 e V1, V2, V3 i centri di gravità e i volumi rispettivamente del cono e dei conoidi parabolico e iperbolico, risulterà
Ma, oltre a questo e altri contributi, il merito principale di Valerio sta soprattutto nell’aver iniziato un percorso di emancipazione dalla considerazione di casi singoli e nell’aver dimostrato teoremi riguardanti intere classi di figure geometriche. Questa prospettiva caratterizzerà il cammino della matematica nel secolo che si apre con l’opera di Valerio: il passaggio da figure ‘nominate’ a figure arbitrarie, e di conseguenza da metodi dimostrativi adattati al singolo caso in esame a teoremi generali, validi per ogni figura immaginabile, e dimostrati una volta per tutte. Su questa strada Valerio è forse il primo a muovere dei passi, certo il primo a percorrere un sensibile cammino.
Dopo di lui, Cavalieri con la teoria degli indivisibili e soprattutto Descartes con la sua geometria delle curve trasformeranno definitivamente la matematica, rivoluzionandone linguaggio e metodi. Come tutti gli innovatori, Valerio si trova in bilico tra due mondi: pur non essendo più nel vecchio, egli non partecipa ancora totalmente del nuovo. Così i metodi generali si trovano mescolati ad argomenti tradizionali, senza che l’autore mostri una netta preferenza per gli uni o per gli altri; una circostanza questa che, unitamente a una redazione certamente affrettata, deve aver contribuito non poco a una sostanziale sottovalutazione dei contributi di Valerio già da parte dei suoi stessi contemporanei.
Ciò è vero in particolare per il metodo che ha portato al centro di gravità del conoide iperbolico, e che Valerio dimostra per arbitrarie figure «in alteram partem deficientes» (De centro gravitatis, cit., ed. 1661, p. 4), ossia aventi tutte le sezioni simili e sempre minori via via che si procede dalla base verso il vertice. Valerio dimostra che se per due di questi solidi le sezioni fatte alla stessa altezza sono sempre nello stesso rapporto – per es., se hanno la stessa area – allora i loro centri di gravità coincidono. Come si è visto, Valerio applica questa proposizione nel secondo libro del De centro gravitatis per ottenere il centro di gravità del conoide iperbolico. Ma poi nel terzo libro, come se fosse incerto sulla validità di un risultato generale, riprende lo stesso problema e lo affronta con i metodi classici, praticamente ridimostrando in questo caso particolare il teorema che aveva già stabilito nel caso generale (Napolitani, Saito 2004).
La teoria degli indivisibili
Il 16 ottobre 1604, Galilei (che era allora professore di matematica presso l’Università di Padova) così scriveva a fra Paolo Sarpi:
Ripensando circa le cose del moto, nelle quali, per dimostrare li accidenti da me osservati, mi mancava principio totalmente indubitabile da poter porlo per assioma, mi sono ridotto a una proposizione la quale ha molto del naturale e dell’evidente; et questa supposta, dimostro poi il resto, cioè gli spazzii passati dal moto naturale essere in proporzione doppia dei tempi, et per conseguenza gli spazzii passati in tempi eguali essere come i numeri impari ab unitate, et le altre cose. Et il principio è questo: che il mobile naturale vadia crescendo di velocità con quella proportione che si discosta dal principio del suo moto; come, v. g., cadendo il grave dal termine A per la linea ABCD, suppongo il grado di velocità che ha in C al grado di velocità che hebbe in B esser come la distanza CA alla distanza BA, et così conseguentemente in D haver grado di velocità maggiore che in C secondo che la distanza DA è maggiore della CA (G. Galilei, Le opere, Ed. nazionale a cura di A. Favaro, 10° vol., 1900, 19683, p. 115).
La dimostrazione, che non è contenuta nella lettera a Sarpi sopra citata, si trova invece in un foglio risalente agli stessi anni, in cui si afferma quanto segue (fig. 2):
Faccia la linea AH qualunque angolo con la AD, e per li punti B, C, D, siano tirate le parallele BE, CG, DH: e perché le linee DH, CG, BE sono tra di loro come le DA, CA, BA, adunque le velocità ne i punti D, C, B sono come le linee DH, CG, BE. Vanno dunque continuamente crescendo i gradi di velocità in tutti i punti della linea AD secondo l’incremento delle parallele tirate da tutti i medesimi punti.
In oltre, perché la velocità con la quale il mobile è venuto da A in D è composta di tutti i gradi di velocità auti in tutti i punti della linea AD, e la velocità con che ha passata la linea AC è composta di tutti i gradi di velocità che ha auti in tutti i punti della linea AC, adunque la velocità con che ha passata la linea AD, alla velocità con che ha passata la linea AC, ha quella proporzione che hanno tutte le linee parallele tirate da tutti i punti della linea AD sino alla AH, a tutte le parallele tirate da tutti i punti della linea AC sino alla AG; e questa proporzione è quella che ha il triangolo ADH al triangolo ACG, ciò è il quadrato AD al quadrato AC (in Le opere, cit., 8° vol., 1898, 19683, p. 373).
Non ci interessa qui discutere il processo attraverso il quale Galilei è indotto ad abbandonare l’errata ipotesi che la velocità sia proporzionale allo spazio percorso e a sostituirla con quella esatta della velocità istantanea proporzionale al tempo, né come da questa ipotesi Galilei deduca la legge del moto. Quello su cui vogliamo porre l’attenzione è il rapporto geometrico tra «tutte le linee parallele tirate da tutti i punti della linea AD sino alla AH» e l’area del triangolo corrispondente ADH. Quello che Galilei ci dice è che il rapporto tra tutte le linee di ADH e tutte le linee di ACG è lo stesso di quello tra i triangoli ADH e ACG; in altre parole, si può stimare la quantità di tutte le linee del triangolo ADH mediante l’area dello stesso triangolo. Da queste considerazioni prenderà le mosse la teoria degli indivisibili, ideata e sviluppata da Cavalieri nella sua Geometria indivisibilibus continuorum nova quadam ratione promota, che dopo una lunga gestazione verrà pubblicata nel 1635.
Nella sua stima della «velocità con che ha passata la linea AD», che è «composta di tutti i gradi di velocità auti in tutti i punti della linea AD», Galilei ha bisogno di valutare la quantità formata da «tutte le linee parallele tirate da tutti i punti della linea AD sino alla AH». Per questo egli prende l’area del triangolo ADH, stabilendo una sorta di equivalenza tra la nuova grandezza «tutte le linee» e l’area della figura relativa.
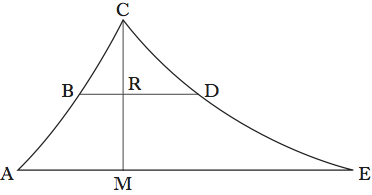
Cavalieri capovolge l’impostazione di Galilei: per calcolare l’area di una figura incognita, o meglio il rapporto tra questa e quella di una figura data, egli valuta il rapporto tra tutte le linee delle due figure. Il nucleo della tecnica consiste nel cosiddetto principio di Cavalieri, esposto nella proposizione IV del secondo libro della Geometria:
Se due figure piane o solide sono collocate sulla medesima altezza; se poi, condotte nelle figure piane linee rette qualunque – e nelle solide piani qualunque – tra loro parallele, rispetto alle quali (o ai quali) si sia presa la detta altezza, si troverà che le porzioni di linee condotte intercette nelle figure piane – oppure le porzioni dei piani condotti, staccate dalle figure solide – sono grandezze proporzionali (prese sempre le grandezze omologhe nella stessa figura); le figure dette staranno tra loro come uno qualunque degli antecedenti sta al suo conseguente che gli corrisponde nell’altra figura (trad. it. Geometria degli indivisibili, a cura di L. Lombardo Radice, 1966, p. 212).
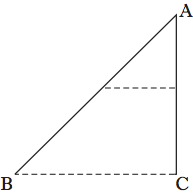
In altre parole, date due figure CAM e CME (fig. 3), se supponiamo che comunque presa una linea BD, il rapporto di BR a RD sia uguale a quello di AM a ME, allora anche le aree delle due figure avranno lo stesso rapporto. Infatti,
come AM sta a ME, cioè come uno degli antecedenti sta a uno dei conseguenti, così staranno tutti gli antecedenti, e precisamente tutte le linee della figura CAM nella direzione di AM, a tutti i conseguenti, ossia a tutte le linee della figura CME (p. 213).
Una volta trovato il rapporto tra tutte le linee delle due figure, è immediato dedurne quello tra le loro aree, perché Cavalieri aveva dimostrato in precedenza che due figure stanno tra loro come tutte le linee della prima a tutte le linee della seconda. Questo teorema, che permette di eliminare completamente la laboriosa riduzione all’assurdo propria dei metodi classici, è alla base di tutti i risultati della Geometria. In particolare, i libri terzo, quarto e quinto sono dedicati alle tre sezioni coniche e ai solidi generati dalla loro rotazione, il sesto (nel quale Cavalieri introduce gli indivisibili curvi) alla spirale, mentre nel settimo libro, aggiunto più tardi, Cavalieri rielabora la teoria per eliminarne alcune imperfezioni.
Ma torniamo alla dimostrazione, il cui punto chiave è l’affermazione che «come uno degli antecedenti sta a uno dei conseguenti, così staranno tutti gli antecedenti […] a tutti i conseguenti». Formalmente, questa non è altro che la proposizione V.12 degli Elementi di Euclide, che recita:
Se delle grandezze qualunque sono in proporzione, come uno degli antecedenti sta a uno dei conseguenti, così tutti gli antecedenti stanno a tutti i conseguenti.
Ma relativamente a Euclide, Cavalieri compie una doppia forzatura: la prima quando applica la proposizione V.12, valida per un numero finito di termini, alle infinite linee della figura; la seconda quando interpreta la frase «tutti gli antecedenti», che nella proposizione euclidea indica chiaramente la loro somma, come «tutte le linee» della figura in questione. Lo stesso Cavalieri era conscio di queste estrapolazioni, dato che non considera terminata la dimostrazione a questo punto, ma continua tentando di giustificare il passaggio dal finito all’infinito:
Infatti il numero indefinito di tutti gli antecedenti e conseguenti, che per le une e per le altre è qui il medesimo, quale che esso sia (le figure infatti sono sulla medesima altezza, e a un qualsivoglia antecedente preso nella figura CAM corrisponde il suo conseguente situato sul suo prolungamento diretto nell’altra figura) non osta a che tutte le linee della figura CAM siano confrontabili a tutte le linee della figura CME, avendo rispetto ad esse un rapporto, come è stato provato; e pertanto tutte le linee della figura CAM, nella direzione AM, staranno a tutte le linee della figura CME, con direzione ME, come AM sta a ME (Geometria degli indivisibili, cit., p. 213).
In definitiva, il teorema riposa su poco più che un’assonanza linguistica tra «tutte le antecedenti» e «tutte le linee», oltre che sull’idea soggiacente a tutto il metodo, un’idea – si badi bene – sempre sottaciuta e non di rado negata, che «tutte le linee» sia un sinonimo di «la somma di tutte le linee».
Si vede qui come una rivoluzione completa sia a volte più semplice di una parziale, e come quello che in un certo contesto era un serio ostacolo possa diventare in un contesto mutato la base sulla quale edificare tutta la teoria. Una volta abbandonato il linguaggio formale ma rigido della teoria delle proporzioni e sostituito con quello molto più duttile anche se meno rigoroso delle manipolazioni algebriche, basterà dotare le linee di Cavalieri di un’altezza infinitesima perché non sia più paradossale il fatto che la somma di un numero infinito di grandezze (ognuna delle quali infinitamente piccola) dia un risultato finito: l’area della figura, cioè la somma degli infiniti rettangolini che la compongono.
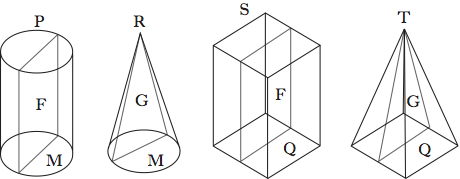
Ma anche con l’ingombro di un formalismo geometrico piuttosto pesante, Cavalieri riesce a calcolare i volumi di un numero considerevole di solidi, tra i quali quelli introdotti due decenni prima da Johannes Kepler (1571-1630). In queste ricerche giocano un ruolo essenziale le nozioni di solido similare e di solidi mutuamente similari. È similare un solido, come il cono, il cilindro, le piramidi, le cui sezioni parallele alla base sono tutte figure simili. Un tale solido si può considerare generato da una delle sezioni in questione e da una seconda figura, che serve per così dire da profilo. Per es., se la sezione è un cerchio e la figura profilo un rettangolo, si ottiene un cilindro; se la sezione è il quadrato ABCD e il profilo il triangolo VEF, si ha la piramide VABCD a base quadrata (fig. 4).
Il principio di Cavalieri consente di calcolare facilmente il rapporto tra due solidi similari con lo stesso profilo. Consideriamo due solidi similari P e S con basi M e Q. Se li tagliamo con un piano, otterremo due figure M1 e Q1 simili alle basi M e Q. Dato che il profilo è lo stesso per i due solidi, le sezioni sono proporzionali alle basi: M1:Q1=M:Q.
Poiché questa relazione vale per ogni sezione, si potrà concludere che il rapporto tra i due solidi è uguale a quello di due qualsiasi delle loro sezioni: P:S=M:Q.
Similmente si può determinare il rapporto tra due solidi similari P e R con diversi profili ma con le stesse sezioni. Sia M la base comune, e siano F e G i due profili. Assieme a questi, consideriamo due altri solidi similari S e T, con gli stessi profili F e G e con basi quadrate Q. I solidi P con S hanno lo stesso profilo e basi M e Q, e quindi per quanto appena visto avremo P:S=M:Q. Analogamente R e T hanno lo stesso profilo e basi M e Q, per cui R:T=M:Q. Di conseguenza P:S=R:T, ossia P:R=S:T.
A parole, il rapporto tra due solidi con profili diversi e la stessa sezione è uguale a quello dei solidi con gli stessi profili e con basi quadrate.
Un risultato elementare può chiarire la portata di questo enunciato. Se prendiamo come profili un triangolo e un rettangolo e come sezione un cerchio, i solidi risultanti sono un cono e il cilindro con la stessa base e la stessa altezza; se invece le sezioni sono quadrati, avremo una piramide e un parallelepipedo rettangolo a base quadrata (fig. 5). Ora, è noto che la piramide è un terzo del corrispondente parallelepipedo; di conseguenza il cono è un terzo del cilindro con la stessa base e la stessa altezza. Il risultato era largamente noto, trovandosi già negli Elementi di Euclide (XI, prop. 10), ma con una dimostrazione particolare e che procedeva mediante riduzione all’assurdo, un procedimento totalmente espunto nella Geometria.
Altri risultati sono più ardui da descrivere e richiedono dimostrazioni solo tecnicamente più complesse. In ogni caso, essi vanno al di là dello scopo di questo scritto. Ma Cavalieri non si limita a esporre una tecnica di ricerca, per quanto efficace; egli vuole fondare una nuova teoria generale, che possa rivaleggiare e sostituire quella degli antichi. Per questo, egli tenta di dare una fondazione geometrica alla teoria degli indivisibili, ancorandola alla geometria classica della quale verrebbe a costituire un’estensione e un perfezionamento.
Come si è visto, la novità della teoria risiede soprattutto nelle nozioni di «tutte le linee di una figura piana» e di «tutti i piani di un solido» e nella loro relazione con l’area o il volume della figura corrispondente. Nella loro formalizzazione, Cavalieri si rivolge naturalmente alla teoria delle proporzioni euclidea, che sola poteva fornire un linguaggio ‘geometrico’, cioè rigoroso, nel quale inserire le nuove classi di grandezze.
Il secondo libro della Geometria è tutto dedicato al tentativo di introdurre, accanto alle figure geometriche, una nuova classe di grandezze che corrispondono, ma che non coincidono con queste ultime. Accanto a ogni figura piana, viene così introdotta una nuova grandezza: «tutte le linee» della figura. E perché la caratteristica principale delle grandezze omogenee è di essere confrontabili tra loro, cioè di avere proporzione, il primo passo sarà di dimostrare il ‘principio di Archimede’, ossia che date due grandezze (cioè tutte le linee di due figure) esiste un multiplo della minore che supera la maggiore.
In mancanza di una definizione operativa delle nuove entità, e soprattutto di criteri per la loro somma e il loro confronto, la dimostrazione non poteva che rivelarsi illusoria, come Cavalieri stesso non mancherà di rilevare, come pure illusoria è la dimostrazione del teorema fondamentale della teoria degli indivisibili, secondo il quale «figure piane hanno lo stesso rapporto che hanno tutte le linee di esse». D’altra parte, tali difetti non inficiano gli sviluppi successivi, dato che, come si è detto, questi dipendono essenzialmente dal principio di Cavalieri, che è indipendente da essi. E in effetti, quando nel settimo libro Cavalieri rivedrà criticamente tutta la sua costruzione, di fatto abbandonerà la teoria generale e si concentrerà sul confronto degli indivisibili distributive, cioè per l’appunto sul principio che porta il suo nome (Giusti 1980).
Sviluppi del metodo degli indivisibili
La potenza del nuovo metodo non poteva mancare di suscitare reazioni e interesse nel mondo scientifico del Seicento. Una parte dei matematici (invero una minoranza, formata da scienziati non di primo piano) lo respingeva in blocco in nome di esigenze di rigore, che non di rado – come per esempio nel caso di alcuni gesuiti – nascondevano posizioni ideologiche e interessi di parte. A questa minoranza si contrapponeva una maggioranza disposta ad accettare e soprattutto a utilizzare un metodo di indiscussa efficacia, vuoi cercando una sistemazione teorica nell’ambito della geometria classica, in questo simile a quanto aveva fatto Valerio nella centrobarica, sia ignorando in toto le questioni fondazionali e servendosi del metodo senza preoccuparsi della sua rispondenza a esigenze di rigore. In questi sviluppi si fanno sentire molto le differenze geografiche: mentre in Italia è ancora viva la lezione della matematica classica, e i successori di Cavalieri si atterranno per lo più alle tecniche messe a punto da lui senza ulteriori innovazioni, in Francia e in Gran Bretagna si assiste a una netta algebrizzazione del metodo, con la progressiva introduzione di elementi infinitesimali.
A grandi linee, possiamo distinguere tre differenti punti di vista, a volte coesistenti nelle opere di uno stesso geometra ma più spesso testimoni di una scuola o quanto meno dell’esistenza di gruppi di scienziati che condividono idee e metodi.
Da una parte, soprattutto in Italia, abbiamo gli stretti seguaci di Cavalieri, dalle cui opere attingono un metodo geometrico che applicheranno a problemi non considerati da quest’ultimo. Su questa strada proseguiranno Stefano Angeli (1623-1697), allievo e correligionario di Cavalieri, che sarà professore all’Università di Padova dal 1662, e tra il 1654 e il 1667 scriverà un considerevole numero di opere, tutte basate sul metodo del maestro, e, con altra efficacia, Torricelli.
Quest’ultimo non si limiterà a estendere i risultati ottenuti da Cavalieri, ma affronterà problemi a quel tempo attuali, che lo vedranno in corrispondenza – e a volte in competizione – con i maggiori matematici dell’epoca. Tra questi problemi, lo studio della cicloide, una curva introdotta da poco in geometria, di cui egli riuscì (indipendentemente dai francesi Gilles Personne de Roberval e Blaise Pascal) a calcolare l’area, e la scoperta del ‘solido iperbolico acuto’, un solido infinito in estensione ma di area finita.
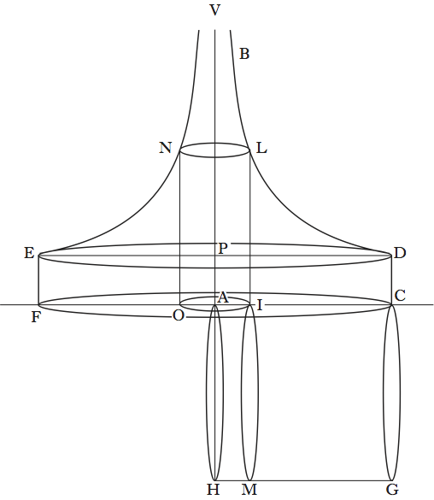
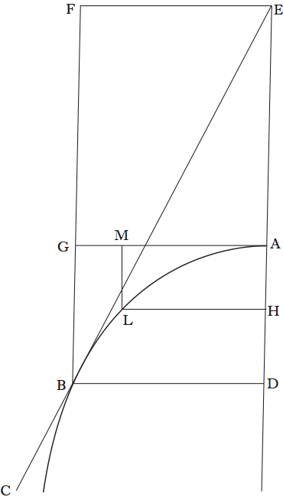
Il solido è quello ottenuto ruotando una iperbole equilatera intorno a un suo asintoto. Se BLD è un’iperbole equilatera, e S è il punto tale che ST=SU, si ha per ogni punto L sull’iperbole AI:ST=ST:IL (fig. 6).
Se indichiamo con RS l’asse dell’iperbole, avremo evidentemente RS=2×21/2ST, e dunque RS2=8AI×IL.
Facciamo ora ruotare l’iperbole intorno all’asintoto AV, e sia VLDCFENV il solido infinitamente lungo generato in questa rotazione, ivi incluso il cilindro di base DCFE (fig. 7). Sia AH uguale all’asse dell’iperbole, e sul cerchio di diametro AH costruiamo il cilindro di altezza AC. Questo cilindro è uguale (in volume) al solido iperbolico.
La dimostrazione di Torricelli fa uso delle superfici cilindriche NLIO come indivisibili curvi. Preso un qualsiasi punto I su AC, la superficie laterale di questo cilindro è data dal prodotto della circonferenza di raggio AI per l’altezza IL. Per quanto detto sopra, questo cilindro è uguale al cerchio di diametro IM=AH=RS.
Poiché ciò è vero comunque si prenda il punto I, avremo che tutte le superfici cilindriche di AC saranno uguali a tutti i cerchi di AC, e quindi il solido iperbolico acuto VLDCFENV è uguale al cilindro ACGH (Opere di Evangelista Torricelli, cit., 1° vol., p. 193).
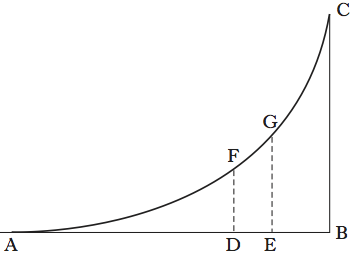
Una seconda tendenza, diffusa soprattutto fuori d’Italia, consiste nel considerare gli indivisibili non come dei segmenti, ma come dei rettangoli con un lato infinitamente piccolo. Il linguaggio è estremamente crudo: si divide la base AB della figura ABC (fig. 8) in infinite parti uguali (di cui una è il segmento infinitesimo DE) e si considera la figura come composta dagli infiniti rettangolini DFGE (si noti che essendo il segmento DE infinitesimo, il lato FG si può considerare orizzontale).
In questo modo si possono calcolare le aree di alcune figure. Per esempio, l’inglese John Wallis (1616-1703) nel suo Arithmetica infinitorum (1655) calcola l’area della parabola dividendo la base AB in infiniti segmenti infinitesimi di lunghezza a=AB/∞ mediante i punti a, 2a, 3a, …, na, … Il rettangolino che ha per base il segmento di estremi na e (n+1)a ha base a e altezza n2a2. Per calcolare l’area della parabola occorrerà sommare tutti questi rettangolini facendo variare n da 1 a ∞, ottenendo
Wallis aveva calcolato la somma dei quadrati dei primi N interi; qui prende N=∞ e ottiene la quantità
Ora il numero 1 si può trascurare rispetto a ∞, e quindi la formula precedente si riduce a
Con lo stesso metodo, Wallis riesce a calcolare l’area di tutte le ‘infinite parabole’ di qualsiasi grado, cioè di equazione y=xn, dimostrando che essa è uguale ad ABn+1/(n+1), un risultato che Cavalieri aveva dimostrato (con l’aiuto del ‘lemma di Beaugrand’) per n=3, 4 e che aveva solo congetturato per le potenze maggiori.
Infine, un terzo e più importante punto di vista consiste nel dotare sì ogni indivisibile di uno spessore infinitesimo, ma di considerare quest’ultimo come variabile. Questo approccio è presente in forma embrionale in alcuni scritti inediti di Torricelli e, in maniera molto più sistematica, in Fermat e Pascal.
Torricelli introduce gli indivisibili a spessore variabile nell’affrontare il problema delle tangenti alle curve di equazione yk=xm. Per Torricelli, a differenza di una linea, che ha solo lunghezza, un indivisibile oltre alla lunghezza ha anche una quantità, che gli proviene dalla sua generazione. Per maggior chiarezza, consideriamo un rettangolo ABCD e sia E un punto della diagonale BD (fig. 9). Se tiriamo le parallele EG ed EF, i trapezi o semignomoni ABEF e CBEG sono uguali in area.
Se ora si divide BE in due parti uguali, e poi in due parti uguali, e così via, e se questa divisione si farà, o si supporrà fatta infinite volte, ci ridurremo ad havere in cambio di semignomoni una linea BC eguale alla BA; dico eguale di quantità non di lunghezza; poiché sebbene indivisibili ambedue sarà la BC tanto più larga della BA, quanto questa è più lunga di quella (Opere di Evangelista Torricelli, cit., 1° vol., p. 322).
Una situazione analoga si ha nel caso delle parabole. Se ABC è una curva di equazione yk=xm, le figure GBLM e DBLH stanno tra loro come k sta a m (fig. 10). Di conseguenza, ragionando come sopra, la quantità della linea GB sta alla quantità della linea BD come k a m. Se ora si traccia la tangente BE in B, la lunghezza ED alla DA sarà come la unghezza FB alla BG, overo come la quantità FB alla [quantità] BG, overo come la quantità DB alla [quantità] BG, cioè come l’esponente [k] all’esponente [m] (p. 323).
Gli oppositori
Come il metodo degli indivisibili aveva suscitato interesse nel mondo scientifico seicentesco, grazie alla sua efficacia e semplicità di applicazione, così la teoria soggiacente, per molti versi oscura e non priva di punti deboli, fu oggetto fin dal suo apparire di critiche anche violente. Questo fenomeno, che spesso accompagna il sorgere di nuove teorie, è accentuato dalla novità e dalla delicatezza della costruzione teorica di Cavalieri, che si spinge a toccare punti molto sensibili della matematica ma anche della riflessione filosofica, quali la composizione del continuo, l’uso dell’infinito attuale, la costruzione geometrica delle figure.
A questi motivi si sovrappongono poi talvolta rancori e invidie private, come nel caso del gesuita bolognese Mario Bettini (1584-1657), ma anche, soprattutto da parte di altri matematici della Compagnia di Gesù, pubbliche affermazioni di preminenza, contro gli indivisibili di Cavalieri, del metodo del centro di gravità introdotto in quegli anni dal gesuita svizzero Paul Guldin (noto come Guldino, 1577-1643) e basato su quello che oggi è noto come teorema di Pappo-Guldino.
Il punto su cui si concentrano tutte le critiche è l’ambiguità del concetto di «tutte le linee di una figura», di cui viene enfatizzato il carattere di insieme infinito, per concludere che in quanto infinite esse non rientrano tra le grandezze che hanno proporzione. Un’obiezione, questa, non nuova a Cavalieri, che ne sentiva il peso fin dalle sue prime riflessioni sugli indivisibili, al punto da chiedere in proposito il parere di Galilei, e che lo aveva spinto a ritornare sul manoscritto della Geometria già pronto per la stampa per aggiungervi quel settimo libro in cui introduce il secondo metodo degli indivisibili. Ora, congiunta all’altra sulla liceità delle dimostrazioni per sovrapposizione, ha l’effetto di muovere ancor più l’ago della bilancia verso quest’ultimo metodo, che assumerà un ruolo centrale nelle Exercitationes geometricae sex (1647). Per il resto, le critiche di Guldino, come pure quelle di Bettini, si possono ridurre al paradosso dei due segmenti AB e AC (fig. 11), che, pur essendo diseguali in lunghezza, hanno i loro indivisibili in corrispondenza biunivoca; un paradosso che Cavalieri aveva risolto introducendo il principio nell’uguale transito, peraltro sistematicamente ignorato dagli oppositori.
Le critiche di Guldino ebbero un’ampia risonanza e provocarono la risposta di Cavalieri, che dedicò loro la terza delle Exercitationes. Meno note, anche perché pubblicate dopo la morte di Cavalieri, furono quelle contenute in un libriccino, dal titolo Exercitatio geometrica de geometria indivisibilium et proportione spiralis ad circulum (1658), del gesuita inglese Thomas White (1593-1676). In esso White attacca il metodo degli indivisibili ripetendo le solite trite obiezioni, ma anche con esempi appropriati e solidi argomenti.
Tra questi, il seguente esempio è tale da gettare seri dubbi sul primo metodo degli indivisibili. Si prendano – dice White – due qualsiasi figure piane tra le medesime parallele, aventi basi uguali e continuamente decrescenti dalla base maggiore verso la minore (fig. 12). I loro indivisibili andranno decrescendo dalle basi inferiori AB=ab verso le superiori CD=cd, e a ogni indivisibile EF della prima figura corrisponderà uno e un solo indivisibile EF dell’altra. Le due figure hanno quindi gli stessi indivisibili, ma le loro aree sono diverse.
Questo esempio, molto più delle critiche di Guldino, inficia definitivamente la validità delle argomentazioni cavalieriane basate su un confronto di «tutte le linee» di due figure prese nella loro totalità. Resta invece valido il secondo metodo degli indivisibili, basato sul principio di Cavalieri. E White, che non si limita nella sua operetta alla parte distruttiva, cercherà di giustificare questo principio riducendolo al metodo degli antichi, a somiglianza di quanto nella seconda delle Exercitationes aveva già fatto lo stesso Cavalieri, e prima di lui Valerio.
Per operare questa riduzione, l’inglese dimostra due proposizioni, l’una logica e l’altra geometrica:
Una dimostrazione ovvero un’operazione, che esclude ogni differenza che si possa opporre, prova l’eguaglianza. […]
A un qualsiasi quanto continuamente decrescente verso il vertice si possono inscrivere sia all’interno che all’esterno, per mezzo di bidivisioni ovvero dimezzamenti dell’asse e delle sue parti, e di corrispondenti linee o piani paralleli alla base, altri quanti che differiscano dal primo per una quantità minore di una posta ad arbitrio […].
[Con questi due risultati non è allora difficile provare che] tutto ciò che si pretende di dimostrare per mezzo di una proposizione espressa nel linguaggio degli indivisibili, si potrà con uguale facilità dimostrare per mezzo di questo metodo, e da esso trae fondamento (Exercitatio geometrica, cit., f. B3r).
Non per questo è tuttavia necessario abbandonare la teoria degli indivisibili, e anzi addirittura se ne possono ritenere le dimostrazioni, avendo l’avvertenza di operare alcuni cambiamenti:
Poiché se necessario si possono costruire sugli indivisibili dei quanti che stanno nella stessa proporzione degli indivisibili, è chiaro che con questi quanti parziali (come si è fatto nel metodo) si può svolgere la dimostrazione con la stessa facilità che con gli indivisibili, ed addirittura sarà costruita allo stesso modo se soltanto si cambieranno le parole, e al posto di l’indivisibile A sta all’indivisibile B si dirà il quanto di base A sta al quanto di base B (f. B4v).
In definitiva, pur partendo da una posizione fortemente critica White si situa a mezza strada tra gli oppositori del metodo e coloro che, convinti della sua fecondità, tentano in qualche modo di riformarlo in modo da renderlo più sicuro e meno esposto a critiche.
Su questa strada si muoveranno soprattutto quei matematici gesuiti, come il fiammingo André Tacquet (1611-1660) o il francese Claude-François Milliet Dechales (o de Chales; 1621-1678), che pur ripetendo le critiche alla teoria non vorranno privarsi di un metodo che ha dato eccellenti prove. Ma ciò avverrà nella seconda metà del Seicento. Ancora pochi anni, e il calcolo infinitesimale affronterà gli stessi problemi con ben altra efficacia, relegando il metodo degli indivisibili e il suo inventore al rango di precursore.
Opere
G. Cardano, Artis magnae, sive de regulis algebraicis liber unus, Norimbergae 1545.
N. Tartaglia, Quesiti et inventioni diverse, Venezia 1546, 1554, 15625.
R. Bombelli, L’algebra parte maggiore dell’aritmetica divisa in tre libri, Bologna 1572; 1a ed. integrale a cura di E. Bortolotti, U. Forti, Milano 1966.
L. Valerio, Liber de centro gravitatis solidorum, Roma 1604, 16612.
B. Cavalieri, Geometria indivisibilibus continuorum nova quadam ratione promota, Bononiae 1635, 16532 (trad. it. Geometria degli indivisibili, a cura di L. Lombardo Radice, Torino 1966).
T. White, Exercitatio geometrica de geometria indivisibilium et proportione spiralis ad circulum, Londini 1658.
G. Galilei, Le opere, Ed. nazionale a cura di A. Favaro, 20 voll., Firenze 1890-1909, 19683.
E. Torricelli, Opere, a cura di G. Loria, G. Vassura, 3 voll., Faenza 1919.
Bibliografia
E. Giusti, Bonaventura Cavalieri and the theory of indivisibles, Bologna 1980.
L. Pepe, Note sulla diffusione della “Géométrie” di Descartes in Italia nel sec. XVII, «Bollettino di storia delle scienze matematiche», 1982, 2, pp. 249-88.
K. Andersen, Cavalieri’s method of indivisibles, «Archive for history of exact sciences», 1985, pp. 291-367.
E. Giusti, La “Géométrie” di Descartes tra numeri e grandezze, «Giornale critico della filosofia italiana», 1987, pp. 409-32.
U. Baldini, P.D. Napolitani, Per una biografia di Luca Valerio. Fonti edite e inedite per una ricostruzione della sua carriera scientifica, «Bollettino di storia delle scienze matematiche», 1991, 1, pp. 3-157.
P. Freguglia, Bombelli, Viète e Descartes: tre momenti dello sviluppo dell’algebra nel Cinquecento, in Lezioni galileiane, 1° vol., Alle origini della rivoluzione scientifica, a cura di P. Casini, Istituto della Enciclopedia Italiana, Roma 1991, pp. 199-218.
E. Giusti, L’algebra nel “Trattato d’abaco” di Piero della Francesca: osservazioni e congetture, «Bollettino di storia delle scienze matematiche», 1991, 2, pp. 55-83.
E. Giusti, Algebra and geometry in Bombelli and Viète, «Bollettino di storia delle scienze matematiche», 1992, 2, pp. 303-28.
P.D. Napolitani, K. Saito, Royal road or labyrinth? Luca Valerio’s “De centro gravitatis solidorum” and the beginnings of modern mathematics, «Bollettino di storia delle scienze matematiche», 2004, 2, pp. 67-124.