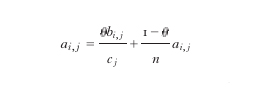ALGEBRA LINEARE

ALGEBRA LINEARE

L'a. l. costituisce uno strumento matematico di importanza fondamentale in ogni disciplina scientifica. Essa costituisce sia un efficace linguaggio comune con cui formulare problemi di natura diversa, sia un ricco bagaglio di metodi di risoluzione per problemi che si incontrano in molte applicazioni. Anche se i suoi fondamenti teorici sono consolidati ormai da molto tempo, gli aspetti computazionali dell'a. l. sono molto più recenti e in continuo sviluppo. Per meglio descrivere i recenti avanzamenti in questa disciplina occorre richiamare brevemente la natura e l'origine dell'a. l. e descriverne i concetti di base.

L'a. l. nasce originariamente dall'esigenza di costruire una teoria per la risoluzione di sistemi di m equazioni lineari in n incognite, cioè del tipo

i=1,2,…,m

in cui gli x_j, per j=1,...,n, sono le incognite del sistema mentre i b_i sono i termini noti. Gli a_i,j sono quantità note chiamate coefficienti del sistema. Il sistema lineare viene scritto in forma più compatta come Ax=b, dove si denota con A=(a_i,j) la tabella di m righe e di n colonne formata dagli a_i,j, con x=(x_i) la n-upla di valori (x₁,...,x_n) e con b=(b_i) la m-upla di valori (b₁,...,b_m). Si usano i termini vettore delle incognite e vettore dei termini noti per indicare rispettivamente x e b,mentre A è chiamata la matrice m×n del sistema; gli a_i,j sono gli elementi di A e i b_i e gli x_i le componenti dei due vettori b e x.

I concetti di vettore e di matrice vanno ben al di là del concetto di n-upla o di tabella di numeri. In effetti il concetto di vettore e più in generale di spazio vettoriale, alla base dell'a. l., è quello di un'entità astratta definita da un insieme di assiomi che ne regolano le operazioni di addizione e di moltiplicazione per un numero. La rappresentazione di un vettore in una particolare base è fornita da una n-upla di numeri. Una base v₁, v₂,..., v_n di uno spazio vettoriale è un insieme minimo di elementi dello spazio che permettono di generare ogni altro elemento attraverso combinazioni lineari, vale a dire mediante espressioni del tipo

v=α₁v₁+α₂v₂+... + α_nv_n

con α₁,..., α_n numeri di un campo (generalmente reali o complessi). Il valore di n è detto dimensione dello spazio vettoriale.

Una matrice A di dimensione m^×n rappresenta invece un'applicazione lineare A dallo spazio vettoriale U di dimensione n nello spazio vettoriale V di dimensione m, cioè un'applicazione che associa a un vettore u di U un vettore v=A(u) di V in modo tale che A(αu+βw)=αA(u)+βA(w) per ogni u,w in U e α, β nel campo. Una volta assegnate due basi u₁,u₂,...,un e v₁,v₂,...,v_m rispettivamente di U e di V, gli elementi a_i,j definiscono univocamente l'azione di A mediante il comportamento sulla base u₁,...,u_n, tramite la relazione

A(u_j) =a_1,jv₁+a_2,jv₂+... +a_m,jv_m

Concetti importanti dell'a. l. sono quelli di determinante, rango, matrice inversa, autovalore e autovettore. In particolare, i concetti di autovalore e di autovettore, che esprimono geometricamente quelle direzioni (autovettori) che sono trasformate in se stesse a meno di un fattore di variazione della lunghezza (autovalore) sotto l'azione della trasformazione lineare rappresentata dalla matrice, hanno un ruolo importante nello studio delle vibrazioni in problemi di fisica, di ingegneria e di calcolo scientifico in genere.

I primi tentativi documentati di risolvere sistemi di equazioni lineari si trovano nel libro cinese Jiuzhang suanshu (Nove capitoli sui procedimenti matematici) datato intorno al 200 a.C. Documentazioni successive si hanno dopo quasi due millenni, quando il matematico giapponese S. Kowa migliorò la tecnica cinese introducendo il concetto attualmente noto come determinante. Circa nello stesso periodo il matematico tedesco G.W. Leibniz sviluppava in modo indipendente il suo concetto di determinante. Sembra che sia nel lavoro di Kowa sia in quello di Leibniz fosse contenuta quella che poi venne chiamata la regola di Cramer per risolvere i sistemi di equazioni. Tra il 1750 e il 1900 fu scritto molto sul concetto di determinante, che diventò lo strumento più importante per risolvere i sistemi lineari. Ma è solo con il lavoro del matematico inglese A. Cayley (1821-1895) che il concetto di matrice fu introdotto come entità a sé stante distinto dal concetto di determinante, assieme alle operazioni algebriche fra matrici. Il lavoro A memoir on the theory of matrices segna la nascita della teoria delle matrici e dell'algebra lineare.

Grandi contributi furono dati dal matematico inglese J.J. Sylvester che aveva introdotto il concetto di rango, termine coniato dal matematico tedesco F.G. Frobenius.

Dopo che la teoria delle matrici si consolidò verso la fine del 19° sec., prese campo la consapevolezza che entità matematiche di natura diversa avevano forti analogie con le matrici, in particolare erano accomunate dalle stesse proprietà algebriche di composizione. Lo studio delle proprietà comuni di entità diverse ha portato alla formalizzazione assiomatica del concetto di spazio vettoriale da parte dei matematici H. Grassmann, G. Peano e H. Weyl.

Algebra lineare numerica

Fin dall'apparire dei primi calcolatori, grande attenzione fu posta sull'applicazione degli strumenti automatici di calcolo alla risoluzione numerica di sistemi di equazioni differenziali ordinarie e alle derivate parziali che erano ricondotti a problemi di algebra lineare. Il corpus di idee, tecniche e algoritmi per il trattamento numerico dei problemi dell'a. l. si è andato sempre più consolidando fino a costituire il fondamento del settore di ricerca noto come algebra lineare numerica. Obiettivi importanti nel futuro dell'a. l. numerica sono sia la sintesi e l'analisi di metodi di risoluzione sia la loro implementazione su calcolatore mediante la realizzazione di software.

La stabilità numerica e la teoria della perturbazione

Nella risoluzione di problemi matematici con un calcolatore si generano errori per l'uso di un'aritmetica approssimata (floating point). Tecniche di fondamentale importanza per la stima degli errori furono introdotte da Wilkinson nei primi anni Sessanta. Lo studio degli effetti causati dagli errori presenti nei dati è detto studio del condizionamento del problema, mentre l'analisi degli errori introdotti dall'aritmetica approssimata è detta analisi della stabilità dell'algoritmo.

L'approssimazione della soluzione mediante metodi iterativi

I metodi iterativi generano una successione convergente alla soluzione data. La scelta di un approccio iterativo può essere dettata da motivi di necessità o di utilità. Dalla irresolubilità per radicali delle equazioni algebriche di grado maggiore di 4, risultato ben noto nella teoria di Galois, segue la necessità di approssimare gli autovalori di matrici con tecniche iterative. Metodi iterativi per la risoluzione di sistemi lineari sono stati invece introdotti per sfruttare le proprietà di sparsità e struttura presenti nella matrice dei coefficienti.

La complessità computazionale degli algoritmi

Una scelta accorta del metodo di risoluzione può consentire una riduzione dei tempi di elaborazione superiore a quella ottenuta con l'avanzamento dell. Grandi progressi nell'efficienza dei metodi numerici di risoluzione per particolari problemi applicativi si ottengono dall'uso di 'proprietà di struttura' del problema. Il settore delllineare numerica strutturata si è andato rapidamente consolidando negli ultimi decenni del 20° secolo.

Metodi diretti per la risoluzione di sistemi lineari

Il problema della risoluzione di un sistema n × n Ax=b è alla base dello sviluppo dell'a. l. numerica. La scelta di un metodo di risoluzione dipende da ulteriori informazioni quali: l'ordine di grandezza di n, la struttura della matrice A, la conoscenza del rango di A e di una misura della sua sensibilità rispetto a perturbazioni degli elementi.

I metodi diretti di uso comune per affrontare questo calcolo sono sostanzialmente tre; 1) il metodo di eliminazione gaussiana con strategie di pivoting; 2) il metodo basato sulla fattorizzazione QR; 3) il metodo di Cholesky per il caso di A definita positiva.

Nel metodo dell'eliminazione gaussiana la matrice A è ridotta in forma triangolare superiore mediante operazioni elementari (combinazioni lineari di righe). La tecnica di pivoting parziale, basata sullo scambio di righe, è introdotta per garantire l'applicabilità del processo e migliorarne la stabilità numerica. Questo metodo conduce al calcolo di una fattorizzazione di matrici PA=LU, con P matrice di permutazione, L triangolare inferiore con elementi diagonali uguali a 1 e U triangolare superiore.

Utilizzando le tecniche di analisi all'indietro dell'errore introdotte da Wilkinson si mostra che la fattorizzazione ottenuta in aritmetica floating point è la fattorizzazione esatta di una matrice perturbata e quindi la soluzione calcolata è la soluzione esatta di un sistema i cui coefficienti sono perturbati.

L'idea della risoluzione del sistema lineare mediante fattorizzazione della matrice dei coefficienti è feconda di generalizzazioni. Una conduce al metodo di fattorizzazione QR basato sulla decomposizione della matrice A nel prodotto di una matrice unitaria Q e di una matrice triangolare superiore R.

Metodi iterativi per la risoluzione di sistemi lineari

I metodi di fattorizzazione generalmente distruggono le proprietà di sparsità e di struttura presenti nella matrice dei coefficienti. Per sistemi di grandi dimensioni l'uso di queste proprietà può rendere trattabili problemi altrimenti intrattabili. In questi contesti i metodi 'iterativi' possono essere vantaggiosi. Tali metodi generano una successione di vettori {x^(k)} convergente sotto opportune ipotesi alla soluzione del sistema dato. Il costo computazionale per il calcolo di x^(k) è generalmente ricondotto al costo della moltiplicazione della matrice A per un vettore. Eventuali proprietà di struttura di A possono essere così utilizzate ad ogni passo. L'efficienza del metodo dipende anche dalle proprietà di convergenza della successione {x^(k)} .

I metodi iterativi classici di Jacobi, Gauss-Seidel e di rilassamento sono basati sull'idea di partizionamento additivo della matrice A e di punto fisso. I metodi multigrid introdotti da Fedorenko e Bakhvalov e sistematizzati da Brandt e Hackbusch si basano su un'idea proveniente dalla discretizzazione di equazioni differenziali. Il termine multigrid si riferisce alla generazione di una gerarchia di griglie (grid in inglese) con parametro di finezza crescente. Metodi correlati sono basati sulla decomposizione dei domini e sulle rappresentazioni wavelet.

Sviluppi importanti riguardano il metodo del gradiente coniugato introdotto da Hestenes e Stiefel e le sue numerose varianti e generalizzazioni. Fra queste le tecniche di precondizionamento per accelerare la convergenza e i metodi di Krylov che includono i metodi di Lanczos, di Arnoldi, GMRES, MINRES e SYMMLQ. Recenti significativi progressi riguardano la sintesi di precondizionatori ad hoc per problemi strutturati.

Problemi di autovalori

Il calcolo degli autovalori di una matrice A, cioè dei numeri complessi Ï per cui esiste un vettore non nullo x tale che Ax=ëx , è in teoria ricondotto alla risoluzione dell'equazione caratteristica p(ë)=det(A−ëI)=0. Questo approccio non è in generale conveniente per motivi di stabilità numerica. Algoritmi più efficaci si basano sul principio di ridurre per similitudine la matrice A ad una forma più semplice dalla quale possono essere estratte agevolmente le informazioni cercate con metodi iterativi.

Il metodo di Jacobi, storicamente il primo metodo che è stato introdotto per il calcolo degli autovalori, conserva notevole interesse per applicazioni al calcolo parallelo.

L'algoritmo di scelta è il metodo QR introdotto da Francis e Kublanovskaya nel 1961 la cui derivazione segue un precedente metodo LR attribuito a Rutishauser. Una estensione del metodo QR per il problema generalizzato agli autovalori Ax=ëBx conduce al metodo QZ di Moler e Stewart. Problemi quadratici e polinomiali sono riconducibili al caso generalizzato. Metodi di bisezione sono introdotti per il calcolo selettivo di autovalori di una matrice tridiagonale hermitiana, metodi divide et impera si prestano ad architetture di calcolo parallelo. Il calcolo degli autovettori può essere svolto utilizzando il metodo delle potenze e le sue numerose varianti.

Il calcolo degli autovalori di matrici di elevate dimensioni e sparse ha imposto un generale ripensamento delle tecniche risolutive. L'uso dei sottospazi di Krylov ha condotto ai metodi di Lanczos e di Arnoldi. Importanti progressi sono rappresentati dalla teoria di Kaniel-Paige per lo studio del metodo di Lanczos in aritmetica finita, dal metodo implicitly restarted e il metodo di Jacobi-Davidson.

Problemi lineari ai minimi quadrati

Essi forniscono una generalizzazione della risoluzione di un sistema lineare Ax=b al caso in cui A è m^×n; consistono nel determinare un vettore x che minimizza la norma euclidea ||Ax−b||. Se A ha rango massimo, il problema si riduce alla risoluzione del sistema delle equazioni normali. I metodi di fattorizzazione LU e QR e la decomposizione ai valori singolari trovano applicazione in questo contesto.

Trasformata discreta di Fourier (DFT)

La DFT (Discrete Fourier Transform) è una trasformazione lineare di vettori associata a una particolare matrice unitaria (matrice di Fourier). Metodi veloci per il suo calcolo, ben conosciuti in letteratura come algoritmi FFT (Fast Fourier Transform), sono basati su fattorizzazioni ricorsive della matrice di Fourier e sebbene già noti a Gauss, sono stati sviluppati algoritmicamente solo a partire dalla metà degli anni Sessanta del secolo scorso da J.W. Cooley e J.W. Tukey.

Le applicazioni della FFT sono numerose e varie; riguardano fra l'altro il vasto campo dell'elaborazione digitale di segnali e immagini e la computer algebra.

Complessità del prodotto di matrici

Il prodotto di matrici n×n si può calcolare con circa 2n³ operazioni aritmetiche con le formule che derivano dalla sua definizione. Alla fine degli anni Sessanta del 20° sec., V. Strassen dimostrò che la complessità della risoluzione di un sistema n × n è asintoticamente la stessa della moltiplicazione di matrici n × n e diede un algoritmo con costo dell'ordine di nω con ω=log₂7⟨2,81. L'estremo inferiore τ dei valori di ω per cui è possibile moltiplicare matrici con un costo dell'ordine di nω non è al momento noto, e vale 2≤τ⟨2,38.

Applicazioni

Si può dire che non c'è campo della scienza in cui l'a. l. non rivesta un ruolo importante; le sue applicazioni sono infatti innumerevoli. Fra le principali si riportano di seguito alcune di quelle che hanno avuto maggiore impulso in epoca recente.

Catene di Markov e processi stocastici

Molti problemi legati al caso sono modellati da catene di Markov. In una catena di Markov un sistema stocastico può trovarsi in un numero discreto di stati diversi. La probabilità di occupare un certo stato dipende solamente dallo stato occupato all'istante precedente e non dalla storia passata. Esempi significativi sono i problemi di ricerca di informazioni sul web e lo studio di modelli di code che si incontrano in vari campi quali per es.: telefonia, traffico su reti di computer, internet, analisi dei rischi. Problema fondamentale è il calcolo del vettore stazionario di probabilità x soluzione dell'equazione x=Ax, dove A=(a_ij) è la matrice di transizione e a_ij è la probabilità di passare dallo stato i allo stato j. Lo studio delle catene di Markov fa ampio uso della teoria di Perron-Frobenius delle matrici non negative e degli strumenti dell'a.l. numerica per il calcolo di x. Strumenti computazionali più avanzati sono i metodi di risoluzione di equazioni di matrici, cioè equazioni in cui i coefficienti e l'incognita stessa sono matrici, e le fattorizzazioni di Wiener-Hopf.

Per quanto riguarda il problema della ricerca di informazioni sul web, il motore di ricerca più efficiente al luglio 2005 è Google. Esso effettua l'attribuzione di un indice di importanza (page ranking) alle singole pagine presenti sul web calcolando il vettore x tale che x=Ax, dove A è una matrice n × n e n è il numero di pagine presenti sul web (circa 8 miliardi al luglio 2005). Numerando le pagine da 1 a n, gli elementi di A sono dati da

dove b_i,j=1 se nella pagina j c'è un link alla pagina i, b_i,j =0 altrimenti; inoltre c_j=b_1,j+…+b_n,j e θ è una costante compresa fra 0 e 1. Questa matrice descrive, attraverso una catena di Markov, il comportamento di un navigatore che si sposta da pagina a pagina seguendo a caso con probabilità θ i vari link presenti nelle singole pagine oppure saltando con probabilità 1−θ a una qualsiasi altra pagina. L'importanza di una pagina viene assegnata in base alla probabilità di essere maggiormente visitata da questo navigatore virtuale e quindi viene data dalle componenti del vettore stazionario di probabilità x tale che x=Ax.

Dopo aver individuato le pagine in base all'argomento cercato, Google le ordina in base alla loro importanza. La costante θ è un fattore correttivo di attenuazione che tiene conto della possibilità che il navigatore non segua più i link contenuti in una pagina.

Elaborazione digitale di segnali e immagini

La codifica digitale dell'informazione ha ormai quasi completamente sostituito l'uso della codifica analogica. In questo settore i metodi di elaborazione, di compressione e di filtraggio di segnali audio e video sono essenzialmente basati su strumenti di a. l., e la trasformata discreta di Fourier insieme ad altre trasformate trigonometriche giocano, in tale ambito, un ruolo essenziale.

I metodi di regolarizzazione di Tikhonov, l'uso di iterazioni su sottospazi di Krylov con tecniche di gradiente coniugato precondizionato, i metodi GMRES e i metodi di Arnoldi permettono di risolvere problemi di restauro di immagini degradate e rumorose (in campo medico e astronomico) in tempi rapidi. Tecniche recentemente introdotte quali il principio di discrepanza e la L-curve forniscono strumenti da utilizzare al fine di regolarizzare meglio la soluzione.

Un'altro problema correlato riguarda il riconoscimento automatico di forme, che viene effettuato mediante l'adattamento del metodo dei minimi quadrati.

Problemi di grandi dimensioni e calcolo scientifico

Numerosi problemi di calcolo scientifico comportano la risoluzione di complesse equazioni differenziali. Esempi a riguardo sono lo studio di fenomeni meteorologici, problemi di fluidodinamica in ambito aeronautico e navale, lo studio di modelli cardiaci e di modelli biologici. Generalmente le matrici che si incontrano hanno proprietà di sparsità, cioè la maggior parte degli elementi sono nulli. Talvolta sono presenti proprietà di struttura. Sono stati sviluppati molti metodi per la risoluzione efficiente di questi sistemi; oltre ai già citati metodi iterativi, sono utilizzati i metodi multigrid.

Una parte importante del calcolo scientifico riguarda il calcolo di autovalori e autovettori di matrici. Questi problemi si incontrano nello studio della stabilità di strutture meccaniche, nel calcolo delle loro frequenze di risonanza e nello studio di sistemi antisismici.

Problemi di robotica industriale conducono alla risoluzione di sistemi di equazioni polinomiali non lineari. Recenti studi di calcolo simbolico e algebra computazionale hanno ricondotto la risoluzione di tali sistemi al calcolo di autovalori di matrici di grandi dimensioni.

Problemi di CAGD (Computer Aided Geometric Design) relativi al calcolo dei punti intersezione di curve nel piano sono ricondotti a problemi agli autovalori generalizzati.

Ricerca di informazioni

La ricerca di documenti che contengano parole chiave richieste dall'utente viene attualmente svolta mediante l'uso della SVD o di altre fattorizzazioni rank-revealing di una matrice A=(a_i,j), dove a_i,j rappresenta la frequenza che la chiave i compare nel documento j.

Teoria del controllo e stabilità

La teoria del controllo (v.) studia la controllabilità e la stabilità di sistemi complessi che evolvono nel tempo. Controllabilità significa capacità di condurre il sistema in uno stato desiderato in un tempo assegnato mediante un insieme di azioni. Si pensi, per es., all'atterraggio di un aereo. Stabilità è la capacità del sistema di ritornare in uno stato di equilibrio una volta che ne viene allontanato. Problemi tipici sono il calcolo della funzione esponenziale di una matrice, determinare se una matrice ha autovalori con parte reale negativa (caso a tempo continuo) o di modulo minore di 1 (caso a tempo discreto), o contare quanti autovalori stanno in una certa regione del piano complesso (calcolo dell'inerzia generalizzata).

Nei problemi di controllo intervengono importanti equazioni di matrici, fra cui le equazioni di Lyapunov, Sylvester e Riccati. Metodi numerici per la risoluzione di questi problemi sono stati sviluppati negli ultimi dieci anni.

Altre applicazioni

Importanti applicazioni dell'a. l. si incontrano in statistica, problemi combinatori, teoria dei grafi, teoria dei giochi, ottimizzazione, economia matematica, biomatematica, sociologia matematica, ingegneria chimica e altre discipline.

Prospettive

La complessità dei modelli matematici del mondo reale, che va di pari passo con l'esigenza di affrontare in modo sempre più preciso e accurato situazioni complesse della vita quotidiana e del calcolo scientifico, ha alimentato e continua ad alimentare la ricerca matematica nel settore dell'a. l. e dell' a. l. numerica. Strumenti classici teorici sviluppati in ogni branca dell'a. l. sono stati affiancati e potenziati da metodi avanzati di risoluzione numerica. I problemi classici agli autovalori si sono arricchiti con i problemi generalizzati e quadratici, motivati dall'esigenza del calcolo delle frequenze di risonanza di struttute meccaniche più complesse. Problemi di calcolo di autovalori sono emersi nella sintesi di materiali, in grado di modificare le loro proprietà di elasticità e rigidità, utilizzati in Giappone per la realizzazione di ammortizzatori intelligenti che contrastino in modo attivo le scosse telluriche su un edificio. Lo studio di modelli di code ha condotto alla introduzione di nuove equazioni di matrici e ai metodi di risoluzione conseguenti. Nuove architteture di calcolo, in particolare i supercomputer paralleli (il Blue Gene della IBM, formato da 128.000 processori che lavorano in parallelo, ha una velocità di calcolo di 360 teraflops cioè di 3,6×10¹⁴ operazioni aritmetiche al secondo) hanno imposto lo sviluppo di metodi di calcolo che traggano la massima efficienza dalla struttura parallela. Lo sviluppo commerciale di sistemi a precisione di calcolo variabile sta dando un notevole impulso alla sintesi di algoritmi adattivi. La peculiarità di ogni singolo problema, che si traduce in proprietà di sparsità e di struttura delle matrici che lo modella, ha portato a un grande sviluppo dell'a. l. numerica strutturata, in cui vengono studiate a livello astratto le specifiche proprietà di struttura e sparsità, al fine di individuare metodi di risoluzione molto più efficienti di quelli di tipo generale che si applicano a matrici qualsiasi. Oltre alle classiche matrici di Toeplitz che intervengono ogni qualvolta è presente nel modello una proprietà di invarianza per traslazione, sono state introdotte e analizzate classi più generali quali le matrici con basso displacement rank e classi di matrici con proprietà di rango quali le matrici quasi-separabili e semi-separabili.

Si prevede quindi una continua e inarrestabile espansione dell'a. l. rivolta alla formulazione di nuovi problemi, allo studio di strutture di matrici e all'analisi delle loro proprietà, animata dalla forte spinta a individuare gli strumenti matematici per la progettazione e l'analisi di metodi di risoluzione sempre più efficienti in un rapporto sinergico con lo sviluppo della tecnologia.

bibliografia

A. Householder, The theory of matrices in numerical analysis, New York 1964.

J.H. Wilkinson, The algebraic eigenvalue problem, Oxford 1965.

M. Kline, Mathematical thought from ancient to modern times, New York 1972.

D. Bini, M. Capovani, O. Menchi, Metodi numerici per l'algebra lineare, Bologna 1988.

R.A. Horn, C.R. Johnson, Topics in matrix analysis, New York 1993.

G. Strang, Introduction to linear algebra, Wellesley (MA) 1993.

G.H. Golub, C.F. Van Loan, Matrix computations, Belmont 1996.

C. Meyer, Matrix analysis and applied linear algebra, Philadelphia 2000.