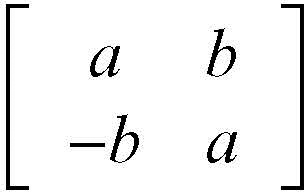algebra [struttura]
algebra [struttura]
algebra (struttura) particolare struttura algebrica definita su un campo K; è uno spazio vettoriale A su K dotato di un prodotto interno bilineare ∗: A × A → A (→ applicazione bilineare). Se il prodotto ∗ è associativo, allora lo spazio vettoriale A si dice algebra associativa, se ∗ è commutativo, allora A è un’algebra commutativa. Se, rispetto alla sua struttura di anello, lo spazio vettoriale A è unitario, se cioè esiste un elemento neutro (indicato con il simbolo 1) per l’operazione ∗, allora A è un’algebra unitaria. Un’algebra unitaria è detta algebra di divisione se ogni suo elemento è invertibile rispetto all’operazione ∗.
Esempi di algebra sono forniti dall’insieme delle matrici quadrate a coefficienti in un campo (→ algebra matriciale), dotato delle usuali operazioni di addizione e moltiplicazione, e dall’insieme degli endomorfismi di uno spazio vettoriale, dotato delle operazioni di addizione e composizione. Queste sono più in particolare esempi di algebre associative unitarie e sono tra loro isomorfe (sono cioè isomorfi gli spazi vettoriali e gli anelli sottostanti; → isomorfismo). In generale, ogni algebra associativa unitaria è isomorfa a una sottoalgebra di un’algebra matriciale: per esempio, l’algebra C dei numeri complessi è isomorfa all’algebra delle matrici 2 × 2 del tipo
dove a e b sono numeri reali.
Un’algebra associativa è detta algebra normata se è uno spazio normato in cui, per ogni coppia di elementi a e b, la norma ‖...‖ soddisfa la disuguaglianza:
Se l’algebra è unitaria, allora in aggiunta si richiede che la norma soddisfi l’equazione ‖1‖ = 1. Un’algebra normata che, come spazio normato, sia uno spazio di Banach è detta algebra di Banach. Un esempio di algebra di Banach commutativa unitaria è dato dall’insieme C0 ([0, 1]) delle funzioni continue sull’intervallo reale [0, 1], assumendo come norma di una funzione il massimo assunto sull’intervallo [0, 1] dal suo valore assoluto (→ Banach, algebra di).