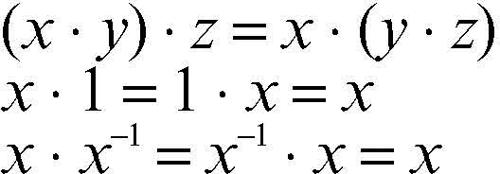algebra universale

algebra universale

algebra universale settore disciplinare, parte dell’algebra e al tempo stesso sua evoluzione, che studia le proprietà comuni alle → strutture algebriche. Ciò avviene assumendo un punto di vista più astratto in cui i concetti di funzione, relazione, operazione e lo stesso quantificatore esistenziale sono ricondotti all’unico concetto di operazione n-aria, cioè di arità n, dove n può essere 0 (e ciò equivale all’esistenza di una costante), oppure 1 (e con ciò si comprendono le funzioni in una variabile) oppure 2 (come le usuali operazioni) oppure un naturale qualunque (ma in alcuni casi si accettano anche operazioni infinitarie). Gli assiomi di ogni particolare struttura sono dunque formulati in termini di identità che devono essere soddisfatte da tutti gli elementi dell’insieme, non vuoto, che è sostegno della struttura stessa. Per esempio, tradizionalmente un gruppo è definito come una coppia (G, ∗), in cui G è un insieme e ∗ un’operazione binaria su G che soddisfa determinati assiomi, tra cui l’esistenza dell’elemento neutro e dell’inverso di ogni elemento. In algebra universale il gruppo è una quaterna (G, ·,⁻¹, 1) in cui · è un’operazione binaria, ⁻¹ un’operazione unaria e 1 un’operazione nullaria (cioè di arità 0 e che designa la costante elemento neutro) e tale che siano sempre soddisfatte le seguenti identità:

Si procede in modo analogo per monoidi, anelli, reticoli e altre strutture algebriche o d’ordine e si danno definizioni comuni per isomorfismo, omomorfismo, immersione o altri concetti utilizzati in molti contesti matematici. In tale modo alcuni teoremi (per esempio quelli relativi agli isomorfismi tra strutture) sono unificati in un unico teorema. Su una linea di analoga spinta alla generalizzazione si muove la teoria delle → categorie.