Algebra

Algebra

sommario: 1. Introduzione. 2. Gruppi in generale. 3. Gruppi semplici finiti. 4. Gruppi infiniti. 5. Gruppi liberi. 6. Gruppi abeliani infiniti. 7. Anelli in generale. 8. Corpi. 9. Algebra lineare. 10. Anelli associativi. 11. Anelli di gruppo e rappresentazioni di gruppi. 12. Anelli non associativi in generale. 13. Anelli alternativi. 14. Anelli di Jordan. 15. Anelli di Lie. 16. Anelli commutativi. 17. Algebra omologica. 18. Categorie. 19. Questioni varie: a) teoria dei reticoli; b) algebre di Hopf; c) K-teoria algebrica; d) semigruppi; e) anelli noetheriani non commutativi; f) algebre su anelli commutativi. □ Bibliografia.

1. Introduzione

Il nostro scopo principale è di tracciare lo sviluppo delle idee più importanti nell'algebra del sec. XX, cercando di inquadrare, per quanto possibile, lo stato attuale della ricerca. Volgeremo cautamente - di tanto in tanto - lo sguardo al futuro, accennando a problemi tuttora aperti e a possibili direzioni di ricerca ad essi collegati.

Non vi è nulla nella matematica di oggi, che non abbia le sue radici nel passato. Pertanto sarà spesso naturale volgerci indietro, al sec. XIX e a periodi ancora più remoti, pur mantenendo molto schematici i riferimenti storici.

L'algebra si trova in un rapporto singolare con il resto della matematica. Nella prefazione al suo libro, Chevalley (v., 1956) scrive: ‟L'algebra non è solo una parte della matematica, ma sostiene nella matematica quel ruolo che la matematica stessa ebbe per lungo tempo nella fisica".

Ricordando, a questo proposito, una osservazione di Wigner sulla ‟irragionevole efficacia" della matematica nelle scienze fisiche, ci si può chiedere se, similmente, l'al- gebra sia irragionevolmente valida per il resto della matematica. Lasciamo la risposta ai fatti.

Viene spesso sottolineata la profondità di astrazione nella matematica del sec. XX. Mentre gli ottimisti la pongono entusiasticamente ad un livello di attività intellettuale senza precedenti, i pessimisti non sono d'accordo e prevedono un periodo di stasi seguito da un periodo oscuro. Ad ogni modo, allo stato attuale delle cose, il dibattito stesso non sembra molto realistico, in quanto l'astrazione ha virtualmente sconfitto i suoi oppositori.

E, in relazione ai diversi rami della matematica, è proprio nell'algebra che l'astrazione ed il metodo assiomatico hanno raggiunto livelli senza precedenti ed hanno avuto i loro più grandi trionfi. Questo è dovuto al fatto che, essendo le strutture algebriche così vicine ai fondamenti, il metodo assiomatico fa miglior presa e può progredire più velocemente. Inoltre queste strutture si presentano così spesso in altre parti della matematica, che l'averle assiomatizzate permette una notevole economia di pensiero. Le due strutture algebriche predominanti, le sole che abbiano effettivamente importanza, sono i gruppi e gli anelli. Probabilmente la maggioranza degli algebristi, se non la loro totalità, concorda su questa affermazione dogmatica. Comunque, è opportuno precisare ulteriormente la situazione.

I gruppi e gli anelli possono essere dotati di strutture addizionali (strutture topologiche, ordinamenti, strutture algebrico-geometriche, insiemi duali di operazioni, ecc.). Un posto d'onore spetta ai moduli, che, in certo qual modo, coinvolgono sia la struttura di gruppo sia quella di anello. Inoltre, esistono modi significativi di indebolire gli assiomi (per es., studiare semigruppi invece di gruppi, o, nel caso degli anelli, sostituire la legge associativa con altre leggi). Vi sono, infine, teorie con un grado elevatissimo di generalità, come la teoria delle categorie e l'algebra universale, che pervadono, in un certo senso, tutta l'algebra, gruppi ed anelli inclusi.

Con tutte queste precisazioni, ritorniamo alla nostra affermazione dogmatica e cominciamo con una parte generale sui gruppi, seguita da alcuni capitoli su vari aspetti speciali della teoria. Faremo lo stesso nella trattazione degli anelli. Seguiranno alcuni capitoli sull'algebra omologica e sulle categorie, ed infine un capitolo sarà dedicato a questioni varie, tra le quali i reticoli, i semigruppi, gli anelli noetheriani ed alcune algebre speciali.

Nella bibliografia, oltre alle pubblicazioni citate nel presente articolo, sono indicati anche quattro trattati di uso molto frequente (Bourbaki, Lang, MacLane e Birkhoff, van der Waerden). Per motivi di spazio, alcuni lavori, anche se citati, non sono stati elencati nella bibliografia, ma ci si è limitati a indicarne il nome dell'autore e l'anno di pubblicazione. Il lettore interessato potrà trovare i riferimenti bibliografici completi desiderati nelle ‟Mathematical reviews" per i lavori dal 1940 in poi, e nel ‟Zentralblatt für Mathematik und Ihre Grenzgebiete" o nel ‟Jahrbuch über die Fortschritte der Mathematik" per i lavori anteriori al 1940.

Purtroppo, in un panorama dell'algebra del sec. XX, è necessario introdurre molti concetti tecnici, che saranno definiti di volta in volta.

2. Gruppi in generale

I sistemi dei numeri razionali e dei numeri reali erano noti in tempi remoti (sebbene i numeri negativi e lo zero lo fossero solo implicitamente). Si può dire che i gruppi che si ottengono da questi sistemi di numeri, usando l'addizione e la moltiplicazione come operazioni, sono stati studiati dai matematici per oltre duemila anni.

Un primo esempio di gruppo in un contesto più sofisticato si trova nell'opera fondamentale che inaugurò la matematica del XIX secolo: le Disquisitiones Arithmeticae di Gauss (1801). Quando Gauss definì la composizione di forme quadratiche binarie, introdusse nella matematica un oggetto (che risultò poi essere un gruppo abeliano finito), nessuna proprietà cruciale del quale poteva consideràrsi evidente a priori; in particolare, la legge associativa non era ovvia. (A questo punto, potremmo accennare al fatto che, più tardi, Dedekind presentò il gruppo in questione in modo più convenzionale, essenzialmente come un gruppo moltiplicativo di ideali in un certo anello).

La teoria dei gruppi giocò un ruolo chiave nelle importanti scoperte di Galois, nelle quali tuttavia intervenivano soltanto i gruppi di permutazioni; l'idea astratta di gruppo apparteneva ancora al futuro, ma erano già poste le nozioni fondamentali di sottogruppo normale, di serie di composizione, di risolubilità.

In un lavoro pubblicato nel 1854, Cayley giunse molto vicino a porre la definizione moderna di gruppo astratto. Gradualmente questo concetto mise le sue radici e l'importante libro di Burnside (v., 1911²), apparso proprio all'inizio del nuovo secolo, pose le basi per il suo sviluppo successivo.

Oggi, gli assiomi di gruppo sono posti di solito come segue. È dato un insieme G, sulla cui natura non si dice nulla, salvo che G ha un'operazione binaria con certe proprietà. Tale operazione è una funzione che assegna ad ogni coppia di elementi a e b di G un terzo elemento di G, che si indica spesso semplicemente con ab.

Si impongono all'operazione binaria tre assiomi: 1) legge associativa (ab)c = a(bc); 2) esistenza di un elemento neutro e, o unità, tale che ea = ae = a per ogni a (l'unicità di e segue immediatamente dalla legge associativa); 3) esistenza per ogni a di un inverso a^-1, tale che aa^-1 = a^-1 a = e (la legge associativa assicura anche l'unicità di a^-1).

Si può di fatto esigere un po' meno, in quanto bastano una unità a destra (ae = a) ed un inverso a destra (aa^-1 = e), oppure, ovviamente, unità ed inverso a sinistra. Ma si presenta a questo punto una complicazione curiosa: assumendo, per esempio, unità a destra e inversi a sinistra, si ottiene qualcosa di più generale che un gruppo, la cui struttura è stata più volte discussa nella letteratura. È possibile dare assiomi per i gruppi senza fare intervenire gli assiomi di esistenza, usando una unica operazione binaria e delle identità soddisfatte da essa; comunque, gli assiomi che ne risultano non sono molto eleganti.

Le nozioni chiave nella teoria dei gruppi sono quelle di omomorfismo, nucleo, sottogruppo normale, gruppo quoziente.

Il concetto di omomorfismo può essere formulato per strutture molto generali. Un omomorfismo è un'applicazione, da una struttura ad un'altra struttura, che conserva quelle proprietà che sono rilevanti per le due strutture. Per i gruppi, un omomorfismo è una applicazione f da un gruppo G ad un altro gruppo, che soddisfa la condizione: f(ab) = f(a)f(b) per tutti gli a e b in G. Non è necessario richiedere che f conservi l'elemento unità e gli inversi perché ciò segue di conseguenza. Il sottoinsieme di G costituito da tutti gli elementi di G la cui immagine mediante f è l'elemento neutro dell'altro gruppo è un sottogruppo K di G, cioè un sottoinsieme di G che è esso stesso un gruppo relativamente alla stessa operazione di G. Il sottogruppo K si chiama nucleo di f. Il nucleo non è un sottogruppo qualunque di G; esso ha una proprietà in più: per ogni a in K e x in G, x^-1ax appartiene a K. Un sottogruppo con questa proprietà si dice ‛normale'. Si può formare il gruppo quoziente, che si denota con GK, di G relativamente ad un sottogruppo normale K, eliminando, in un certo senso, gli elementi di K ogniqualvolta essi compaiono.

Un omomorfismo biunivoco è un isomorfismo; un isomorfismo di un gruppo su tutto se stesso è un automorfismo.

La presenza di un sottogruppo normale K in un gruppo G ci permette una ‛decomposizione' di G nei due gruppi K e GK. In tal modo possiamo ridurre, in molti casi, dei problemi su O a problemi analoghi su K e su GK, e questo ci induce a considerare quei gruppi che non hanno sottogruppi normali (eccetto, ovviamente, i due sottogruppi ‛banali' costituiti, rispettivamente, da tutto G e dall'insieme che ha come unico elemento e).

Il seguente teorema è dovuto a Lagrange: se G è un gruppo finito ed H è un suo sottogruppo, l'ordine di H (l'ordine di un gruppo finito è il numero degli elementi che esso contiene) divide l'ordine di G. Pertanto, un gruppo il cui ordine sia un numero primo non ha sottogruppi non banali, né normali né non normali; un tale gruppo non è interessante. Perciò diciamo che un gruppo è semplice se, oltre a non avere sottogruppi normali non banali, non è neppure finito di ordine primo. L'uso del termine ‛semplice' è in questo caso paradossale, perché lo studio dei gruppi semplici è di fatto molto complicato. Nel prossimo capitolo torneremo su questo argomento.

3. Gruppi semplici finiti

Nel discutere la struttura dei gruppi semplici finiti, cercheremo di seguire lo sviluppo di tale argomento fino ai nostri giorni. Cominciamo con gli esempi classici, esaminando anzitutto il gruppo S_n delle permutazioni di n elementi, il cosiddetto gruppo simmetrico di grado n. Per n ≤ 4, questi gruppi sono all'estremo opposto della semplicità: sono ‛risolubili'.

Un gruppo G si dice ‛commutativo' o ‛abeliano' se ab = ba per tutti gli a e b in G (il nome ‛abeliano' è in onore del matematico norvegese Abel per il suo lavoro del 1829, che tratta, per dirla con linguaggio moderno, di equazioni algebriche aventi un gruppo di Galois abeliano; v. il cap. 8 di questo articolo). G si dice ‛risolubile' se può essere ottenuto da un numero finito di gruppi abeliani, cioè se esiste una catena di sottogruppi

G = G₀ ⊃ G₁ ⊃ G₂ ⊃ ... ⊃ G_n = e,

tale che ogni G_i+1 sia normale in G_i ed ogni G_i/G_i+1 sia di ordine primo. L'aggettivo ‛risolubile' deriva dal legame, posto in luce dalla teoria di Galois, con la risolubilità di una equazione algebrica per radicali. Effettivamente, il fatto che le equazioni polinomie in una variabile siano risolubili per radicali esattamente fino al quarto grado trova la sua spiegazione nella risolubilità di S_n per n ≤ 4.

Per n ≥ 5, S_n non è più risolubile e non è neppure semplice, anche se gli manca poco ad esserlo. Infatti S_n ha un solo sottogruppo normale proprio; esso consiste di tutte le permutazioni pari, viene chiamato il ‛gruppo alterno' di grado n ed è indicato con A_n. (Una permutazione è pari se la si ottiene con un numero pari di scambi successivi di due elementi; si può dimostrare che l'essere tali scambi in numero pari è indipendente dal modo in cui essi vengono effettuati). Il gruppo A_n è semplice ed il suo ordine è n!/2.

I gruppi alterni A_n, per n≥ 5, formano la nostra prima famiglia infinita di gruppi semplici finiti classici. Per avere altri esempi di gruppi semplici, consideriamo i gruppi di matrici e partiamo dal gruppo lineare GL_n(F) di tutte le matrici n × n non singolari su un corpo F (per informazioni sui corpi, v Clifford e Preston, 1961 e 1967). Il gruppo GL~(F) non è semplice, ma possiamo ottenere da esso un gruppo semplice effettuando delle opportune ‛riduzioni'. Con una prima riduzione si sostituisce a GL_n(F) il gruppo unimodulare (o lineare speciale) SL_n(F), consistente delle matrici n × n con determinante 1; una seconda riduzione si ottiene considerando il gruppo quoziente di SL_n(F) rispetto al suo centro (il centro di un gruppo consiste degli elementi che commutano con ogni elemento del gruppo; nel nostro caso è il sottogruppo delle matrici scalari). Otteniamo così il gruppo unimodulare proiettivo, che una volta si indicava con PSL_n(F) ed oggi più semplicemente con L_n(F). Questo gruppo è semplice per tutti gli F e gli n, eccetto che in due casi bizzarri: quando n = 2 ed F è il corpo di 2 o 3 elementi. Così, quando F è finito, otteniamo la nostra seconda famiglia infinita di gruppi semplici finiti classici.

Queste due famiglie esauriscono i primi pochi gruppi semplici finiti, come è illustrato nella tabella seguente. (Nella nostra notazione F_q è l'unico corpo finito con q elementi; q deve essere una potenza di un numero primo).

A questo punto, senza entrare nei dettagli, enunciamo brevemente i fatti rimanenti. Nello studio dei gruppi di Lie (gruppi topologici, nei quali un intorno dell'identità può essere parametrizzato da uno spazio euclideo in modo che le Operazioni di composizione del gruppo siano analitiche) esiste una classificazione dei gruppi ‛semplici' (mettiamo ‛semplice' tra virgolette, perché, nel contesto dei gruppi di Lie, ha un significato un po' differente). Tale classificazione risale a Killing e Cartan. Vi sono dei gruppi puramente algebrici, analoghi ai gruppi suddetti, che si possono costruire su un corpo arbitrario F; L_n(F) ne è un esempio. Ma le cose si complicano quando F non è algebricamente chiuso. Questo caso richiede opportune varianti ‛contorte' dei gruppi di Lie semplici; il più facile a descriversi è il gruppo unitario, che si ottiene ‛contorcendo' il gruppo lineare. Richiese parecchio tempo agli algebristi selezionare i fatti rilevanti e portare a compimento la costruzione; a tal fine, ebbe un ruolo importante un lavoro di Chevalley del 1955, esposto diffusamente da Cartan nel 1965. Oggi, il concetto di gruppo semplice finito ‛del tipo di Lie' è pienamente chiarito.

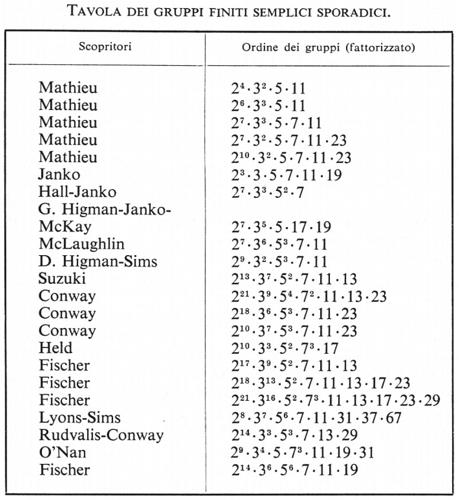
Vi sono altri gruppi semplici finiti, oltre i gruppi alterni ed i gruppi del tipo di Lie? La risposta è affermativa. Nel 1861, Mathieu trovò altri cinque gruppi, indicati di solito con M₁₁, M₁₂, M₂₂, M₂₃, M₂₄ (ove l'indice si riferisce al numero degli elementi che appaiono in una loro rappresentazione naturale come gruppi di permutazione). Poi, per oltre 100 anni, non si trovarono altri gruppi semplici; sicché fu una vera sorpresa quando, nel 1965, Janko ne scoprì uno di ordine 175.560. Da allora ne sono venuti fuori numerosi altri, indicati collettivamente con l'appellativo di ‛sporadici', termine già usato da Burnside (v., 1911², p. 505) per i gruppi di Mathieu. Lo studio dei gruppi semplici sporadici è un'area che si sta sviluppando molto rapidamente, ed è quasi certo che la seguente tavola dei 22 gruppi finora conosciuti sarà già superata quando apparirà questo articolo. Tuttavia, l'argomento è così interessante che vale la pena di dare le informazioni più recenti disponibili fino ad ora. (Recentemente, Fischer ha scoperto altri tre candidati al ruolo di gruppo semplice sporadico, ma la conferma è ancora incerta).

Il problema è se il numero dei gruppi sporadici sia infinito o no. Per ora anche gli studiosi della teoria dei gruppi preferiscono non azzardare congetture.

Oltre alla scoperta di gruppi sporadici, la conoscenza dei gruppi semplici finiti ha fatto tre grandi passi avanti negli anni dal 1961 ad ora; il secondo ed il terzo sono dovuti a J. Thompson, il primo a Thompson in collaborazione con W. Feit.

Risolubilità dei gruppi di ordine dispari. - Un modo equivalente di enunciare questo teorema fondamentale è: tutti i gruppi semplici finiti hanno ordine pari.

La dimostrazione fu completata nel 1961, e venne pubblicata nel 1963 sul ‟Pacific journal of mathematics".

Classificazione dei gruppi semplici minimali. - Un gruppo semplice minimale è un gruppo semplice i cui sottogruppi propri sono tutti risolubili. Il teorema afferma che l'elenco completo dei gruppi semplici minimali consiste di certi gruppi L₂(q), dei gruppi di Suzuki e di due altri gruppi. (Nel 1962, Suzuki scoprì una famiglia di gruppi semplici i cui ordini sono primi con 3. In seguito, i gruppi di Suzuki risultarono essere del tipo di Lie). Il lavoro di Thompson sta per essere pubblicato in una serie di sei memorie, delle quali solo le prime due sono apparse fino a questo momento (1968, 1970).

La classificazione dei gruppi semplici minimali offre alcuni corollari, tra i quali i seguenti due sono particolarmente espressivi. 1) Se ogni sottogruppo di G, generato da due elementi, è risolubile, allora G stesso è risolubile; 2) un gruppo non risolubile contiene due elementi a, b tali che gli ordini di a, b, ab sono a due a due primi tra loro.

Gruppi semplici con ordine primo con 3. - Nel 1972, Thompson annunciò di avere dimostrato completamente che i soli gruppi di questo tipo sono quelli di Suzuki.

Sono interessanti i commenti di Burnside (v., 1911², p. 503) al primo e al terzo teorema: ‟Il contrasto [...] suggerisce inevitabilmente che non esistono gruppi semplici di ordine dispari". Ed ancora a p. 330, dopo avere osservato che i gruppi semplici di ordine pari hanno ordini divisibili per 12 o per 56: ‟Un esame degli ordini dei gruppi semplici non ciclici conosciuti mostra il fatto notevole che sono tutti divisibili per 12". Ma, prudentemente, Burnside si astenne da qualsiasi congettura.

Oggi si sta lavorando intensamente e su un vasto fronte intorno alla teoria dei gruppi semplici finiti. Lo spirito di tali ricerche è il seguente: si pongono condizioni di vario tipo su un ipotetico gruppo semplice finito, soprattutto sui suoi elementi di ordine due o sui suoi sottogruppi del tipo 2-Sylow (sottogruppi il cui ordine è la più elevata potenza di 2 che divide l'ordine del gruppo). Quindi si trovano tutti i gruppi con le proprietà date, con argomentazioni spesso ingegnose ma mai brevi. A volte, sorprendentemente, salta fuori un gruppo sporadico.

Un'esposizione eccellente della situazione di questa teoria fino al 1970 fu fatta da Feit negli Atti del Congresso Internazionale di Nizza (v. anche gruppi).

4. Gruppi infiniti

La teoria dei gruppi infiniti ha un sapore ben diverso da quella dei gruppi finiti. È vero che le nozioni di ‛semplicità' e di ‛risolubilità' conservano il loro significato, sebbene, per quanto riguarda la seconda, vi siano varie nozioni di ‛risolubilità transfinita' che attraggono l'attenzione. È anche vero che i gruppi alterni e quelli del tipo di Lie trovano degli analoghi tra i gruppi infiniti, ma gli algebristi sono ben lontani dall'averne un quadro adeguato. I gruppi infiniti sono troppi e, forse, essi non saranno mai completamente classificati.

La questione è del tutto differente se ci limitiamo a gruppi con qualche struttura addizionale significativa. Tra i gruppi così ‛arricchiti', i più importanti sono i gruppi algebrici e quelli topologici; ma essi vanno oltre lo scopo del presente lavoro (si veda in proposito l'articolo gruppi).

Importante è il problema se un gruppo, soggetto ad una o più delle condizioni soddisfatte da tutti i gruppi finiti, sia necessariamente finito. A questo proposito, il problema di Burnside, posto da Burnside nel 1902, è il più famoso. Esso si presenta in due diversi stadi.

A. Il problema illimitato di Burnside. Se G ha un numero finito di generatori e tutti i suoi elementi sono di ordine finito, G è finito?

B. Il problema limitato di Burnside. Se G ha un numero finito di generatori ed esiste un r tale che x^r = 1 per tutti gli x in O, O è finito?

Il problema illimitato di Burnside fu risolto da Golod nel 1964, come sottoprodotto del notevole lavoro che egli fece in collaborazione con Shafarevich e che condusse ad un esempio di ‛torre infinita di corpi di classi' nella teoria dei numeri algebrici. Allo stesso tempo, Golod diede un controesempio all'analogo del problema illimitato di Burnside nella teoria degli anelli, come sarà indicato nel cap. 10.

Dopo alcune comunicazioni preventive, modificate successivamente, nel 1968 Adjan e Novikov pubblicarono una dimostrazione del fatto che il problema limitato di Burnside ha una risposta negativa quando r è dispari e maggiore o uguale a 4.381. Si tratta di un grosso lavoro complicato, con più di cento lemmi.

La risposta al problema limitato di Burnside è affermativa per r = 2 (banale), r = 3 (Burnside, 19p2), r = 4 (Sanov, 1940) e r = 6 (Marshall Hall, 1957). È possibile che in tutti gli altri casi la risposta sia ‛negativa'.

Osservazione. Nel caso r = 3, Burnside non diede correttamente l'ordine del gruppo; l'errore fu corretto da Levi e van der Waerden nel 1932.

5. Gruppi liberi

Vi è un tipo di gruppo che è, in un certo senso, all'estremo opposto dei gruppi finiti. Tali gruppi sono i gruppi liberi.

Daremo una descrizione semplificata del gruppo libero a due generatori: x e y. In primo luogo, essendo generato da x e y, ogni suo elemento può scriversi nella forma ... xⁱyⁱx^ky^m .. dove i, j, k, m... sono interi (positivi, negativi o nulli). La condizione che ne fa un gruppo ‛libero' è che queste espressioni siano ragionevolmente uniche; non possiamo richiederne incondizionatamente l'unicità, perché il termine x⁰ può essere soppresso ed allora le due potenze di y vicine ad x⁰ a sinistra ed a destra possono essere unite e, nel caso siano della forma yⁱ e y^-i, possono essere soppresse anch'esse, e così via.

Dare una buona definizione di gruppo libero e provarne l'esistenza comporta una certa quantità di difficoltà tecniche, tutt'altro che insormontabili. Una costruzione di questo tipo è usata spesso nella matematica moderna, soprattutto in algebra. A seconda del contesto, la si può descrivere come la costruzione di un oggetto libero soggetto a certe costrizioni, o come la soluzione di un conveniente problema universale.

Vi sono nei gruppi liberi alcuni problemi che sembrano molto semplici, ma che risultano sorprendentemente difficili, per esempio: il fatto che a² = b² implica a= b, è vero in un gruppo libero, ma è tutt'altro che facile da dimostrare.

I gruppi liberi sono utili nello studio dei gruppi in generale. Per esempio, sia G un gruppo generato dagli elementi g_i (in numero finito o infinito). Costruiamo il gruppo libero F con generatori x_j, con un x_i per ogni g_i. Allora (e questa è una proprietà cruciale dei gruppi liberi) esiste un unico omomorfismo di F su tutto G, che manda x_i su g_i per ogni i. Pensando al nucleo K di questo omomorfismo come a qualche cosa che descrive le relazioni tra i generatori g_i di G, si parla di una presentazione di G per mezzo di generatori e relazioni.

Tale modo di presentare un gruppo ha un'applicazione suggestiva nella teoria dei nodi (probabilmente al lettore basta l'idea intuitiva di nodo; per un topologo, un nodo è un omeomorfismo di un cerchio nello spazio euclideo a tre dimensioni). È facile leggere, da un conveniente diagramma rappresentante un nodo, quali sono i generatori e le relazioni per il gruppo fondamentale del complementare del nodo. Quest'ultimo gruppo è l'invariante più importante legato ad un nodo e gli studiosi di teoria dei nodi hanno trovato metodi potenti per analizzare generatori e relazioni di gruppi, con un particolare interesse per i gruppi speciali che si trovano nella teoria dei nodi.

Molta attenzione richiede il dimostrare che ogni sottogruppo di un gruppo libero è libero. Sotto ipotesi di finitezza si può migliorare l'enunciato dicendo che, se G è libero con n generatori ed H è un sottogruppo di G di indice k (ciò significa che G è esattamente l'unione di k sottoinsiemi della forma Ha, chiamati classi laterali destre di H in G), allora H è libero con k(n − 1) + 1 generatori.

La questione ha legami complessi con la topologia. In topologia, ad ogni spazio topologico è assegnato un gruppo, detto gruppo fondamentale (che abbiamo già nominato in relazione ai nodi). Il termine ‛grafo' significa, grosso modo, una collezione di punti, alcuni dei quali sono uniti da segmenti; ad ogni grafo è associato uno spazio topologico molto semplice che i topologi chiamano ‛un complesso di dimensione uno'. Esiste un teorema secondo cui il gruppo fondamentale di un grafo è un gruppo libero; in base ad esso si ottiene una bella dimostrazione del teorema sui sottogruppi dei gruppi liberi (inclusi i dettagli quantitativi sul numero dei generatori).

6. Gruppi abeliani infiniti

Come già si è detto, un gruppo si dice abeliano se l'operazione di gruppo è commutativa. Questa terminologia ha alcuni aspetti peculiari. Si usa ancora spesso l'espressione ‛gruppo commutativo', e nessuno, salvo rare eccezioni, parla di ‛semigruppi abeliani' o di ‛anelli abeliani'. Inoltre il termine ‛varietà abeliana' riguarda tutt'altra parte del lavoro di Abel (una varietà abeliana è un gruppo algebrico connesso, la cui varietà soggiacente è completa: in questo caso, secondo un teorema non banale, l'operazione di gruppo - contrariamente a quanto potrebbe far pensare l'aggettivo ‛abeliana' - non è commutativa).

Nei gruppi abeliani si usano di solito i simboli: + per indicarne l'operazione di composizione, O per l'elemento neutro e − a per indicare l'inverso di un elemento a.

Due aspetti nella teoria dei gruppi abeliani vanno messi in rilievo a questo punto. Secondo il primo, il caso finito è completamente conosciuto: ogni gruppo abeliano finito è somma diretta di gruppi ciclici. Pertanto, in questo campo, soltanto nel caso infinito vi è ancora terra da esplorare. Il secondo aspetto notevole è il ruolo particolare che viene svolto dalla numerabilità, come diremo fra breve.

Nella teoria dei gruppi abeliani ha importanza centrale il concetto di ‛torsione', nel senso che un gruppo può essere ‛di torsione' o ‛privo di torsione' (oppure ‛misto'). La definizione è molto semplice: un gruppo si dice di torsione se consiste di elementi di ordine finito, e privo di torsione se ogni elemento non nullo ha ordine infinito. Ogni gruppo abeliano G contiene un unico gruppo di torsione T massimale, ed il gruppo quoziente G/T è privo di torsione. Un gruppo di torsione è primario (per p primo) se l'ordine di ogni suo elemento è una potenza di p. Secondo un teorema abbastanza semplice ogni gruppo abeliano di torsione può essere scritto in un sol modo come somma diretta di gruppi primari. (Nota: le nozioni di ‛torsione', ‛privo di torsione' e ‛primario' hanno senso anche per gruppi arbitrari, ma non sussistono le relative decomposizioni).

Per quanto riguarda la teoria dei gruppi abeliani primari, il caso numerabile è completamente conosciuto, mentre pochi e frammentari sono i risultati per il caso non numerabile. Il teorema di struttura per i gruppi abeliani primari numerabili è dovuto a Ulm (1933). Tale teorema fa intervenire, in modo essenziale, sia i numeri cardinali sia quelli ordinali, ed è un po' troppo complicato per poterlo qui riportare.

Basterà citare un caso particolare, molto più semplice, scoperto da Prüfer (1923). Diciamo che un gruppo abeliano primario G non ha elementi di altezza infinita se l'intersezione dei sottogruppi pⁿG (n = 1, 2, 3,...) è 0. Si ha il risultato seguente: un gruppo abeliano primario numerabile che non ha elementi di altezza infinita è somma diretta di gruppi ciclici; risultato che non sussiste senza l'ipotesi di numerabilità. Il caso di un gruppo abeliano primario qualunque (cioè non numerabile), anche se privo di elementi di altezza infinita, sembra al di là delle nostre possibilità di indagine per il semplice fatto che di gruppi siffatti ne esistono troppi.

Vi sono poi parecchi risultati, sia pure isolati, per i gruppi abeliani privi di torsione e per quelli misti (cioè gruppi abeliani che non sono di torsione, né privi di torsione). Si può anche definire il concetto di ‛libero' in modo appropriato ai gruppi abeliani. I gruppi abeliani liberi presentano però ben pochi problemi nuovi, in quanto sono somme dirette (eventualmente infinite) di copie del gruppo additivo degli interi. Vale ancora il fatto che i sottogruppi dei gruppi abeliani liberi sono liberi, e la dimostrazione è molto più semplice che nel caso non commutativo, discusso nel capitolo precedente.

Una esposizione completa sui gruppi abeliani è data nel libro di Fuchs (v., 1970 e 1973).

7. Anelli in generale

Un anello è un insieme dotato di due operazioni, dette addizione e moltiplicazione ed indicate nel modo usuale. Per l'addizione, l'anello deve essere un gruppo abeliano; inoltre, si richiede che l'addizione sia connessa alla moltiplicazione dalle due leggi distributive:

a(b + c) = ab + ac (b + c) a = ba + ca.

Per la moltiplicazione, gli algebristi non sono d'accordo se sia meglio richiedere o no un elemento neutro, detto ‛unità' (e cioè un elemento, che viene anche indicato col simbolo 1, tale che 1a = a1 = a per ogni a). Per i nostri propositi, considereremo qui soltanto gli anelli dotati di un elemento unità (salvo che nel cap. 15 sugli anelli di Lie e nella parte dedicata alla K- teoria, v. cap. 19, § c).

Non abbiamo ancora detto nulla sulla legge associativa della moltiplicazione: (ab)c = a(bc); di solito il termine ‛anello' è usato tacitamente per ‛anello associativo'. Se si esclude l'associatività, si parla di ‛anello non associativo', per quanto sarebbe più appropriato dire ‛anello non necessariamente associativo'.

L'esperienza fatta nel XX secolo, suggerisce che vi sono tre classi di anelli non associativi che vale la pena di studiare: gli anelli alternativi (che generalizzano un poco quelli associativi), gli anelli di Lie e quelli di Jordan. Dopo aver parlato degli anelli associativi (v. cap. 10), dedicheremo un capitolo a ciascuna di queste classi di anelli non associativi. (v. capp. 13, 14 e 15).

Dal confronto fra la struttura di gruppo e quella di anello, si è portati a ricercare, per la struttura di anello, i concetti analoghi a quelli di ‛sottogruppo' e ‛sottogruppo normale'. Il primo ci è fornito dalla nozione di ‛sottoanello', che è un sottoinsieme chiuso rispetto alle operazioni dell'anello (e di solito si richiede che contenga anche l'elemento unità dell'anello). Per il secondo, si hanno tre nozioni: ‛ideale sinistro', ‛ideale destro' e ‛ideale bilatero'. Per esempio, un ideale sinistro I, in un anello R, è un sottoinsieme di R che è un sottogruppo additivo e che soddisfa la condizione: RI ⊂ I, cioè I assorbe la moltiplicazione a sinistra per elementi arbitrari di R. La definizione di ideale destro è analoga; un ideale è bilatero se è contemporaneamente un ideale sinistro e destro. Gli ideali bilateri sono gli analoghi dei sottogruppi normali, essi coincidono con i nuclei degli omomorfismi, e, se I è bilatero, si può formare un anello quoziente R/I.

Concludiamo questo capitolo accennando all'importante concetto di modulo su un anello associativo R. Un modulo A su R è un gruppo abeliano additivo, che ammette una moltiplicazione (a sinistra, per fissare le idee) fra gli elementi di A e gli elementi di R in modo che i prodotti che così si ottengono siano ancora in A. In modo forse un po' impreciso ma espressivo, si può dire che gli assiomi sono tutti quelli che postulano tutte le possibili leggi associative.

La nozione di sottomodulo B di A è quella ovvia, e possiamo costruire in modo naturale un modulo quoziente A/B.

I moduli contribuiscono ad illustrare il ruolo degli ideali unilateri nella teoria degli anelli. Infatti, un ideale sinistro in un anello R non è che un sottomodulo di R, quando si considera R come modulo sinistro su se stesso.

8. Corpi

I corpi costituiscono uno dei capisaldi per la costruzione di anelli. Essi forniscono l'ossatura dell'algebra lineare moderna e servono a chiarire e semplificare numerose questioni nell'algebra classica. Perciò è conveniente iniziare lo studio dettagliato degli anelli con un capitolo dedicato ai corpi.

Un corpo è un anello nel quale gli elementi non nulli costituiscono un gruppo rispetto alla moltiplicazione; se tale gruppo moltiplicativo è anche commutativo, allora si parla di corpo commutativo, o campo. Nel seguito useremo sempre il termine ‛corpo', senza specificare se il corpo considerato sia commutativo o no, poiché ciò apparirà chiaro, di volta in volta, dal contesto. Esempi fondamentali sono i corpi dei numeri razionali, dei numeri reali, dei numeri complessi e degli interi modulo p per ogni numero primo p.

Lo studio dei corpi incomincia con l'osservazione che ogni corpo K contiene un unico sottocorpo minimo, detto il suo sottocorpo primo, che è il corpo dei numeri razionali oppure quello degli interi modulo p, per un certo p. In questi due casi, si dice che la caratteristica di K è 0 o p rispettivamente. (Si può definire in modo analogo la caratteristica di un anello arbitrario, ma non entriamo qui nei dettagli).

A partire da un corpo dato, si possono ottenere altri corpi costruendo degli ampliamenti. Quando si amplia un corpo K ad un nuovo corpo K(u) aggiungendogli un elemento u, si presentano due casi: u non soddisfa nessuna equazione algebrica a coefficienti in K, e allora u si dice trascendente su K, altrimenti si dice che u è algebrico su K. Partendo dal sottocorpo primo di un corpo K si può ottenere tutto K con una successione (in generale transfinita) di aggiunzioni di elementi.

Si dice che K è algebricamente chiuso se non ammette ampliamenti algebrici. Dal teorema fondamentale dell'algebra (dimostrato per la prima volta da Gauss) sappiamo che il corpo dei numeri complessi è algebricamente chiuso. La struttura di un corpo algebricamente chiuso è banale, in quanto un tale corpo è determinato dalla sua caratteristica e dal numero dei suoi elementi (nel senso dei numeri cardinali infiniti di Cantor).

Per quanto possa sembrare che la teoria dei corpi non presenti molti problemi, in essa rimangono di fatto molti lati oscuri. Eccone uno, indicato da Zariski, sul quale non si è fatta, fino ad ora, nessuna luce. Siano K ed L due corpi, siano x e y due indeterminate sia su K sia su L, e supponiamo che K(x) e L(y) siano isomorfi. Seguirà da ciò che K e L sono isomorfi? La risposta, fino a questo momento, non si conosce.

La teoria dei corpi è utile per sistemare e semplificare questioni concernenti gli ampliamenti algebrici. Un esempio significativo è lo studio delle costruzioni con riga e compasso nella geometria euclidea. Qui è necessario disporre del concetto di grado [L:K] di un corpo L, ampliamento di K; esso è la dimensione di L come spazio vettoriale su K (si veda il capitolo successivo, dedicato all'algebra lineare). Dati tre corpi K ⊂ L ⊂ M, se [L:K] e [M:L] sono finiti, anche [M:K] è finito ed è uguale a [M:L]•[L:K]. Data una successione di corpi F₁, F₂, ..., F_n, ..., se è soddisfatta la condizione F₁ ⊂ F₂ ⊂ ... ⊂ F_n ⊂ ..., si parla di ‛catena ascendente'; se si inverte il segno di inclusione, si parla, invece, di ‛catena discendente'; se la successione è finita si usa anche il termine ‛torre' in luogo di ‛catena'. Nel caso particolare K ⊂ L ⊂ M si ha dunque una ‛torre ascendente'.

Compiuto il passaggio opportuno dalla geometria all'algebra, il risultato è che, partendo da punti con coordinate razionali, possiamo raggiungere un certo punto, mediante una costruzione con riga e compasso, se, e solo se, le sue coordinate appartengono ad un corpo N, all'ultimo posto di una torre ascendente di corpi, ognuno dei quali sia un ampliamento quadratico del corpo precedente, e alla base della quale è il corpo dei numeri razionali Q. Pertanto [N:Q] è una potenza di 2. Supponiamo ora di voler dividere l'angolo di 600 in tre parti uguali; dovremmo poter mettere cos 20° in una tale torre, il che è impossibile in quanto [Q(cos 20°):Q] è 3.

Un secolo fa le idee in proposito erano fondamentalmente le stesse di oggi, ma il tipo di ragionamento appariva più ingombrante, e richiedeva un esame dettagliato della natura di un numero costruito con una torre di radici quadrate. Oggi, il ragionamento è reso scorrevole dall'uso sistematico del grado di un corpo e dal teorema del prodotto per una torre di tre corpi.

La teoria degli ampliamenti di dimensione finita di corpi è dominata dalla teoria di Galois. In linguaggio moderno, l'idea di Galois fu di studiare una coppia di corpi K ⊂ L, introducendo il gruppo G di quegli automorfismi di L che lasciano fisso ogni elemento di K. È chiaramente possibile che G lasci fissi altri elementi oltre quelli di K; se il sottocorpo fisso è esattamente K, allora si dice che L è normale su K. Il teorema più importante della teoria di Galois asserisce che esiste una corrispondenza biunivoca tra tutti i sottogruppi di G e tutti i corpi che stanno tra K e L, e che, inoltre, tale corrispondenza ha altre proprietà interessanti. Questo teorema ci dà la possibilità di ridurre molte questioni della teoria dei corpi, a priori inaccessibili, a questioni della teoria dei gruppi, dove si hanno già alcune informazioni. Per esempio, possiamo vedere subito che vi è solo un numero finito di corpi intermedi tra un corpo ed un suo ampliamento normale; questo fatto, tradotto nel linguaggio della teoria dei gruppi, dice semplicemente che un gruppo finito ha un numero finito di sottogruppi.

L'applicazione più spettacolare della teoria di Galois (applicazione che ispirò lo stesso Galois) è la dimostrazione che le equazioni algebriche di grado maggiore o uguale a 5 non sono in generale risolubili per radicali, cioè mediante estrazioni di radici ennesime combinate con operazioni razionali. Si dimostra, più in generale, che, se L è normale su K, L è ottenibile da K aggiungendo radicali se, e solo se, il gruppo di Galois di L su K è risolubile. Così, il problema di risolvere le equazioni algebriche per radicali si riduce al fatto (menzionato nel cap. 3) che il gruppo simmetrico S_n è risolubile se e solo se n ≤ 4.

La teoria di Galois presenta varie questioni non ancora risolte, tra le quali emerge la seguente: dato un gruppo finito G, esiste un ampliamento normale del corpo dei numeri razionali con gruppo di Galois isomorfo a G? Per scelte particolari di G, la risposta è nota ed è affermativa; esempi sono dati dal gruppo simmetrico S_n, dal gruppo alterno A_n e da tutti i gruppi risolubili. Inoltre, se si è liberi di scegliere il corpo iniziale, non è difficile trovare una coppia di corpi il cui gruppo di Galois sia un qualsiasi gruppo finito preassegnato. A tale scopo, si parte da un corpo k e gli si aggiungono n indeterminate, ottenendo così il corpo L = k(x₁, x₂, ..., x_n). Il gruppo simmetrico S_n agisce su L permutando tra loro le x_i ed il corpo K, che esso lascia fisso, è il corpo di tutte le funzioni razionali simmetriche nelle x_i con coefficienti in k. Il corpo L è normale su K con gruppo di Galois S_n. Sappiamo, dalla teoria di Galois, che ogni sottogruppo di S_n è il gruppo di Galois di L su un conveniente corpo intermedio; poiché ogni gruppo finito può essere considerato come un sottogruppo di qualche S_n, si può vedere così ogni gruppo finito come un gruppo di Galois.

Nell'esempio suddetto, K, al pari di L, è ‛puramente trascendente' su k, cioè possiamo ottenere K aggiungendo a k certe indeterminate indipendenti (i polinomi simmetrici fanno al nostro caso). Nel 1916, Emmy Noether pose la questione se ciò fosse ancora vero per ‛ogni' corpo tra K ed L. Il problema restò senza risposta finché nel 1969 Swan diede un controesempio. Il gruppo, nell'esempio di Swan, era sorprendentemente semplice: il gruppo di ordine 47 che agisce permutando ciclicamente le 47 variabili.

Terminiamo questo capitolo accennando al teorema di Lüroth, che è connesso con la suddetta questione posta da E. Noether. Un secolo fa, Lüroth dimostrò che ogni corpo tra k e k(x), dove k è un corpo arbitrario ed x è una indeterminata su k, è puramente trascendente su k. L'esempio di Swan serve anche a dare una risposta negativa alla stessa questione posta per corpi tra k e k(x₁, ..., x_n); in effetti la risposta è già negativa per n = 2. Se supponiamo che k sia algebricamente chiuso e di caratteristica 0, la risposta è affermativa per n = 2, come dimostrarono Casteinuovo e Zariski; ma, appena facciamo un passo avanti, incontriamo degli ostacoli: la risposta è di nuovo negativa se n = 3 e k è il corpo dei numeri complessi. Ciò fu dimostrato nel 1972, con l'impiego di metodi elevati tratti dalla geometria algebrica, da Clemens e Griffiths e, indipendentemente, da Iskovskibh e Manin.

9. Algebra lineare

Da un punto di vista generale, l'algebra lineare è il risultato di una fusione dei concetti di corpo e di modulo; in altre parole, uno spazio vettoriale è un modulo su un corpo. La struttura di uno spazio vettoriale a dimensione finita è completamente determinata da un numero cardinale, la sua dimensione, cioè il numero degli elementi di una sua base. Pertanto, l'algebra lineare non si sofferma a studiare gli spazi vettoriali per se stessi. L'interesse nasce quando si considera una trasformazione lineare di uno spazio vettoriale in se stesso o un'applicazione lineare di uno spazio vettoriale in un altro. Una trasformazione lineare è una applicazione che conserva tutte le operazioni di spazio vettoriale; possiamo descriverla come un omomorfismo tra moduli, per rendere più chiaro come essa rientri nella teoria generale degli anelli. Una volta assegnate delle basi negli spazi vettoriali, si può far corrispondere ad ogni trasformazione lineare una tabella (di solito rettangolare) di elementi del corpo, detta ‛matrice'; la matrice si trasforma opportunamente al cambiare delle basi. Questo modo di pensare ad una matrice, come corrispondente ad una trasformazione lineare, che è invece indipendente dalle basi, è risultato molto utile per una comprensione concettuale della teoria delle matrici. Per esempio, il prodotto ‛ per colonne' di matrici, che altrimenti sembra così artificiale, diventa del tutto naturale.

Il punto di vista delle trasformazioni lineari ha portato, attorno al 1920, dopo che i concetti di anello e di modulo erano stati sufficientemente precisati, all' osservazione che la teoria di una sola trasformazione lineare (di uno spazio vettoriale in se stesso) e la teoria dei gruppi abeliani finiti sono entrambi aspetti di un'unica teoria: quella dei moduli su un anello R a ideali principali (cioè un dominio di integrità in cui ogni ideale sia principale) con un numero finito di generatori. Per quanto riguarda i gruppi abeliani basta prendere come anello R quello degli interi; per la trasformazione lineare, R è k [x], anello dei polinomi nella indeterminata x su un corpo k.

Il teorema che afferma che ogni modulo finitamente generato su un anello a ideali principali è una somma diretta di moduli ciclici (cioè di moduli con un solo generatore) - se applicato al caso della trasformazione lineare (supponendo, per semplicità, che il corpo dei coefficienti sia algebricamente chiuso) - fornisce un risultato che è forse quello più utile nella teoria delle matrici: la forma canonica di Jordan. Essa afferma che ogni matrice, dopo un cambiamento opportuno di basi, può essere scritta in blocchi della forma:

e che tale decomposizione è essenzialmente unica.

Per mantenere in limiti ragionevoli questo capitolo dedicato all'algebra lineare, saremo costretti a compiere delle scelte in favore di certi argomenti, tralasciandone molti altri, pure importanti. Porremo l'accento sulle strutture addizionali di cui può esser dotato uno spazio vettoriale e sui modi di combinare tra loro più spazi vettoriali.

Per quanto riguarda quest'ultima possibilità, hanno grande importanza il prodotto tensoriale ed il prodotto esterno. Essi possono essere descritti nel modo più rapido ricorrendo alle basi (anche qui, sarebbe preferibile sviluppare la teoria senza l'uso delle basi, perché il ricorso a queste ultime non è possibile quando i prodotti tensoriali ed esterni sono definiti su anelli generali).

Siano V e W due spazi vettoriali, con basi {v_i} e {w_j} rispettivamente; i simboli v_i ⊗ w_j formano una base del prodotto tensoriale V ⊗ W. Il prodotto esterno è definito su un solo spazio vettoriale V, e una sua base consiste dei simboli v_i ⋀ v_j (i ⟨ j). Una proprietà fondamentale del prodotto esterno è che x ⋀ x = O per ogni x in V. Ai prodotti tensoriale ed esterno sono legate opportune combinazioni di trasformazioni lineari, ed una conveniente potenza esterna di una trasformazione lineare T dà una elegante definizione concettuale del determinante di T.

La principale struttura addizionale che si può imporre ad uno spazio vettoriale su un corpo k è la presenza di una forma quadratica, alla quale è associata una forma bilineare simmetrica; le due forme sono equivalenti se la caratteristica del corpo è diversa da 2. Per semplicità, ignoriamo il caso in cui la caratteristica è 2, e definiamo una forma bilineare simmetrica, che scriviamo con le parentesi (, ), in uno spazio vettoriale V su un corpo k. Si presuppone la linearità di (x, y) in x e la simmetria: (x, y) = (y, x). La forma è non-singolare se (x, V) = O implica x = 0; l'ipotesi di non-singolarità è solo un'innocua normalizzazione.

Tali forme appaiono un po' in ogni parte della matematica. La loro struttura è molto sensibile al corpo base k. Si può trovare sempre (nel caso di dimensione finita) una base diagonale, cioè una base {u_i} tale che (u_i, u_j) = O per i ≠ j, ma gli elementi a_i = (u_i, u_i) sono ben lontani dall'essere invarianti. Se ogni elemento in k è un quadrato, possiamo prendere tutti gli a_i uguali ad 1; se k è un corpo ordinato in cui ogni elemento positivo è un quadrato (l'esempio principale è ovviamente il corpo dei numeri reali), possiamo prendere alcuni a_i uguali a 1, gli altri a −1, ed il teorema di Sylvester asserisce che il numero degli uni e degli altri è invariante. Nel caso in cui il corpo di base sia finito si può fare senza grandi difficoltà una trattazione completa delle forme quadratiche; se è quello dei razionali si ha una sottile teoria dovuta a Minkowski (1890), che fu poi nuovamente trattata in modo elegante da Hasse (1923) e che è valida, più in generale, per i cosiddetti ‛corpi globali' nella teoria dei corpi di classe (corpi di numeri algebrici o corpi di funzioni algebriche in una variabile su un dato corpo finito).

Le forme quadratiche su un corpo arbitrario furono studiate per la prima volta in modo completo nel 1937 in un lavoro di Witt, che appartiene oramai ai classici; poi per trent'anni vi furono ben pochi progressi. L'argomento prese nuovo vigore in una serie di notevoli articoli di Pfister (1965-1967). Indichiamo sommariamente alcuni dei risultati notevoli sulle somme di quadrati, che derivano dal lavoro di Pfister.

L'identità (a² + b²)(c² + d²) = (ad + bc)² + (ac − bd)², che si verifica immediatamente ricordando come si moltiplicano fra loro i numeri complessi, mostra che le somme di due quadrati sono chiuse rispetto all'operazione di moltiplicazione. Una identità analoga alla precedente si utilizza per moltiplicare somme di quattro quadrati; la sua scoperta, avvenuta prima di quella dei quaternioni di Hamilton, che servono a spiegarla, è dovuta a Eulero. I numeri di Cayley, che prendono il nome dal loro scopritore, sono un esempio di come sia possibile moltiplicare somme di otto quadrati. Quando nel 1903 Hurwitz mostrò che una composizione ‛di questo tipo' è possibile per somme di n quadrati soltanto per n = 1, 2, 4 o 8, sembrò di essere giunti alla fine della strada. In modo più preciso, il teorema di Hurwitz si enuncia come segue: se le somme di n quadrati sono chiuse rispetto alla moltiplicazione in un qualsiasi anello commutativo, allora n = 1, 2, 4 o 8.

La situazione rimase a questo punto per settant'anni, quando nel 1965 improvvisamente Pfister riuscì a moltiplicare somme di 2^r quadrati per ogni r. Quale era la spiegazione? Non vi è contraddizione tra il lavoro di Pfister e quello di Hurwitz: il fatto è che il risultato di Pfister è valido solo quando l'anello commutativo che si considera è anche un corpo.

I teoremi di Pfister hanno applicazioni interessanti a questioni concernenti le somme di quadrati nei corpi; per descrivere tali applicazioni, introduciamo un concetto dovuto ad Artin e a Schreier. Un corpo è formalmente reale se -1 non è somma di quadrati nel corpo. Artin e Schreier dimostrarono inoltre che un corpo è formalmente reale se, e solo se, può essere ordinato. Supponiamo ora che il corpo F non sia formalmente reale, così che 1 sia una somma di quadrati in F. Sia m il più piccolo numero di quadrati in F aventi per somma -1. Il lavoro di Pfister condusse alla dimostrazione della congettura seguente: m è una potenza di 2 ed ogni potenza di 2 può essere un tale m. (Pfister chiamò m lo Stufe di F, che è stato tradotto con ‛livello').

Nel 1900, al Congresso Internazionale Matematico di Parigi, David Hilbert propose una lista di 23 problemi ai matematici del XX secolo. Il 17° era il seguente. Sia f un polinomio con coefficienti reali, tale che, per tutti i numeri reali a₁, a₂, . . ., a_n f(a₁, a₂, . . ., a_n) ≥ 0; f è necessariamente una somma di quadrati di funzioni razionali? (Osservazione: Hilbert stesso aveva dimostrato precedentemente che non ci si poteva aspettare di scrivere f come somma di quadrati di polinomi. Alcuni decenni più tardi, T. Motzkin e R. M. Robinson trovarono degli esempi semplici ed espliciti; l'esempio di Motzkin è 1 − 3x²y² + x⁴y^{2 +} x²y⁴). Usando la teoria di Artin-Schreier dei corpi formalmente reali, nel 1927 Artin risolvette affermativamente il problema di Hilbert, ma il metodo di Artin non era costruttivo e non dava nessuna stima del numero dei quadrati di funzioni razionali che occorrevano. Pfister, sviluppando ulteriormente le idee di Artin, dimostrò in modo molto semplice che, per un polinomio in n variabili, sono sufficienti 2ⁿ quadrati. Per n > 2, rimane aperta la questione se questa sia la stima migliore possibile. (Il caso n = 1 è ovvio; nel caso n = 2 Cassels, Ellison e Pfister nel 1971 mostrarono che il polinomio di Motzkin richiede 4 quadrati). Ciò che si sa, d'altra parte, è che possono occorrere n + 1 quadrati, perché Cassels (1964) provò che 1 + x1² + ... + x²_n non può essere somma di un numero di quadrati minore di n + 1.

In questa nostra esposizione potrebbero essere inclusi molti altri temi attuali dell'algebra lineare. Alcuni di questi appaiono in varie applicazioni, specialmente nell'analisi numerica. Altri costituiscono uno sviluppo autonomo dell'algebra lineare, ma si presteranno certamente ad applicazioni future. Di essi daremo soltanto due esempi.

1. (Frobenius). Una matrice quadrata A ad elementi reali positivi ha una sola radice caratteristica avente il massimo valore assoluto, ed essa è reale e positiva. Questo risultato si collega a molti altri teoremi. Questa teoria delle matrici positive è stata usata in economia ed in fisica.

2. Sia B = (bij) una matrice n × n reale e antisimmetrica. Esistono allora n numeri u₁, u₂, ..., u_n , non tutti nulli e tutti ≥ 0, tali che Σ b_iju_j ≥ 0 per ogni i. (Questa è l'essenza del teorema di von Neumann sull'esistenza di un valore per il gioco della somma-zero per 2 persone). La trattazione conclusiva della teoria dei giuochi è stata data nel libro di von Neumann e Morgenstern (v., 1953³).

10. Anelli associativi

Un'algebra è un anello che è anche uno spazio vettoriale su un corpo, ed in cui sono soddisfatte tutte le condizioni naturali di associatività.

Dapprima furono studiate intensamente solo le algebre con dimensione finita. Di fatto, le prime furono le algebre di Lie, poiché la teoria dei gruppi continui ne stimolò lo studio. Per opera di Molien, Killing e Cartan si giunse ad una teoria virtualmente completa della struttura delle algebre di Lie, che ancor oggi resta valida, in forma pressoché inalterata, e della quale ci occuperemo nel cap. 15. Questo studio sistematico delle algebre di Lie confluì in quello delle algebre associative, deformandone temporaneamente l'aspetto. Il quadro cambiò improvvisamente e in modo spettacolare all'apparire degli articoli di Wedderburn all'inizio del XX secolo. La teoria delle algebre associative (di dimensione finita) assunse ben presto una forma vicina a quella di oggi.

Illustriamo ora gli aspetti essenziali di questa teoria. In un'algebra associativa A di dimensione finita su un corpo F, vi è uno ed uno solo ideale bilatero N, dotato delle seguenti proprietà: N consiste di elementi nilpotenti; N contiene ogni ideale (sinistro, destro o bilatero) costituito di elementi nilpotenti (un tale ideale si dice nil); N è nilpotente, cioè esiste un intero r tale che ogni prodotto di r elementi di N è O ed infine, nell'algebra A/N non vi sono ideali nil ≠ O. L'ideale N si dice il radicale di A; se N = O, A si dice semisemplice. L'algebra A/N è semisemplice.

La teoria prosegue con un teorema secondo cui ogni algebra semisemplice si può scomporre in modo unico come somma diretta di algebre semplici (dove un'algebra A si dice semplice se non ha ideali bilateri eccetto O ed A), escludendo il caso in cui sia A² = O ed A abbia dimensione 1. (Da notare il perfetto parallelismo con il caso dei gruppi, dove i gruppi ciclici di ordine primo sono esclusi dalla lista dei gruppi semplici).

Il terzo passo nella teoria di Wedderburn descrive la struttura delle algebre semplici. Teorema: un'algebra semplice A è l'algebra di tutte le matrici n × n su un'algebra con divisione, per un n univocamente determinato, l'algebra con divisione essendo determinata da A a meno di isomorfismi (un anello con divisione è un anello i cui elementi non nulli formano un gruppo moltiplicativo; esso differisce da un corpo per il fatto che la moltiplicazione può essere non commutativa. Naturalmente un'algebra con divisione è un anello con divisione che è anche un'algebra su un corpo).

È utile ora introdurre il centro di un anello R: esso è l'insieme di tutti gli elementi di R che commutano con ogni elemento di R. (Il concetto è esattamente lo stesso per i gruppi, v. cap. 3). Il centro di un anello con unità e semplice, al pari del centro di un anello con divisione, è un corpo. Si consideri un anello con divisione D che abbia dimensione finita sul suo centro Z. Un teorema afferma che la dimensione di D è un quadrato, e che ogni quadrato può effettivamente presentarsi.

Riassumendo, i teoremi di Wedderburn portano a due strutture fondamentali opposte fra di loro: le algebre nilpotenti e le algebre con divisione. Per arrivare a conoscere tutte le algebre associative di dimensione finita vi sono tre passi da compiere: classificare tutte le algebre nilpotenti (su un dato corpo F), classificare tutte le algebre con divisione, ed infine mostrare come si possano connettere fra di loro le algebre così classificate. Esaminiamo ordinatamente queste tre fasi.

1. Non si conosce molto sulle algebre nilpotenti, e si può prudentemente predire che ciò resterà vero ancora per un periodo di tempo considerevole. Esse sfuggono ad ogni tentativo di classificazione, data la grande quantità in cui si presentano. Ciò, comunque, non significa che non sia possibile scoprire teoremi importanti sulle algebre nilpotenti.

2. La natura di un'algebra con divisione D su F è molto sensibile alla scelta del corpo F. Esempio: se F è algebricamente chiuso, D coincide con F. Secondo esempio: se F è il corpo dei numeri reali, D è il corpo dei numeri reali o quello dei numeri complessi oppure è l'algebra con divisione dei quaternioni (teorema di Frobenius).

3. Se F è finito, D è commutativa (è il celebre teorema di Wedderburn secondo cui ogni anello finito con divisione è un corpo).

Sia ora F un corpo globale (si è fatta brevemente menzione dei corpi globali nel capitolo precedente in connessione con il teorema di Minkowski-Hasse sulle forme quadratiche). Un teorema di Brauer, Hasse e Noether (1931), detto a ragione Hauptsatz (‛principio') dai suoi autori, determinò la struttura di un'algebra con divisione su F. (Un ulteriore contributo a questo lavoro fu dato da Albert). Tra l'altro, questo teorema generalizza la parte essenziale del teorema di Minkowski-Hasse. La sua dimostrazione richiede un impiego massiccio di tecniche sia di teoria dei numeri sia di algebra. Concentreremo la nostra esposizione sulla parte riguardante l'algebra.

Brauer, Hasse e Noether dimostrarono che ogni algebra con divisione su un corpo globale è ciclica. Esamineremo le algebre cicliche un po' più avanti in questo capitolo, introducendo, anzitutto, due concetti pertinenti: i prodotti incrociati e il gruppo di Brauer. Uno dei modi di introdurre l'argomento dei prodotti incrociati è offerto dallo studio dell'algebra con divisione dei quaternioni. Questa è un'algebra di dimensione 4 sul corpo dei numeri reali con base 1, i, j, k e la cui moltiplicazione è determinata dalla relazione i² = j² = k² = −1, ij = −ji = k, e dalle altre due analoghe relazioni che si ottengono permutando i, j, k ciclicamente. Poiché k = ij, possiamo prendere come generatori dei quaternioni i e j. L'elemento i genera una copia del corpo dei numeri complessi, in cui l'automorfismo interno indotto da j coincide con il coniugio, poiché j^-1ij = −i. (Ogni elemento x, invertibile in un anello, dà luogo ad una applicazione che associa, ad ogni elemento a, l'elemento x^-1ax; essa è un automorfismo interno. Allo stesso modo possono definirsi gli automorfismi interni nei gruppi).

Questa descrizione dei quaternioni può generalizzarsi fino ad ottenere i prodotti incrociati; ci accontenteremo di un'approssimazione della definizione rigorosa. Sia dato un corpo K, normale e di dimensione n su un corpo di base F e con gruppo di Galois G. Aggiungiamogli degli elementi tali che gli automorfismi interni, che essi inducono, coincidano con gli elementi di G. Accordandoci convenientemente sul modo di moltiplicare i nuovi elementi (ciò introduce un cosiddetto ‛insieme quoziente'), otteniamo una algebra A di dimensione n², che è semplice e centrale (cioè A è semplice ed il suo centro è F); A è detto un prodotto incrociato. Nei casi favorevoli, A è un'algebra con divisione.

Per circa cinquant'anni, rimase aperto il seguente problema, in genere considerato l'unico problema veramente importante nelle algebre associative di dimensione finita: ogni algebra con divisione è un prodotto incrociato? Nel caso particolare delle algebre associative di dimensione ≤ 16, la risposta è affermativa, come fu dimostrato da Wedderburn ed Albert (per i dettagli, v. Albert, 1939, pp. 177-182). Nel 1971, Amitsur rispose però negativamente alla questione generale. Fino ad ora, la più piccola dimensione per un'algebra con divisione che non sia un prodotto incrociato è 64; ed è data appunto dall'esempio di Amitsur nella dimensione più bassa.

Se il gruppo di Galois, che interviene nella costruzione di un prodotto incrociato, è ciclico, diciamo che l'algebra è ciclica. Questa è la definizione di algebra ciclica promessa dianzi, che occorre per il teorema di Brauer-Hasse-Noether.

Se si vuole ulteriormente procedere nella classificazione delle algebre con divisione sui corpi globali, il gruppo di Brauer è molto utile. Consideriamo tutte le algebre semplici centrali su un dato corpo F. Usiamo il prodotto tensoriale come operazione binaria e conveniamo di scartare le matrici non appena esse compaiono, mantenendo solo la struttura di divisione delle algebre. Ne risulta un gruppo abeliano, detto ‛gruppo di Brauer'. Su un corpo globale, il gruppo di Brauer è una somma diretta di copie del gruppo additivo dei razionali modulo 1, con la restrizione che la somma degli elementi sia 0. Quest'ultima legge è detta la ‛legge di reciprocità' ed infatti è una generalizzazione potente della reciprocità quadratica.

Giungiamo infine al terzo punto della teoria di Wedderburn: combinare la parte radicale con quella semisemplice. A ciò provvede un quarto teorema di Wedderburn, che viene chiamato di solito il ‛teorema principale di Wedderburn'. Se A è un'algebra con radicale N, secondo questo teorema, esiste una sottoalgebra S di A, tale che A è uno spazio vettoriale somma diretta di N e S (naturalmente S è isomorfo ad A/N, e pertanto è semisemplice). Questo teorema non fornisce una riduzione completa della teoria ai casi nilpotente e semisemplice, perché abbiamo ancora bisogno di conoscere come S agisce su N; tuttavia esso è certamente una semplificazione sostanziale.

Il teorema di Wedderburn sussiste con l'ipotesi aggiuntiva della separabilità di A/N. Quest'ultima ammette varie definizioni, ma è forse più semplice sostituire il concetto con uno preso dalla teoria dei corpi.

Sia u algebrico su un corpo K e sia f il suo polinomio irriducibile su K. Si dice che u è separabile su K se f non ha radici multiple. Questo è automatico se la caratteristica di K è 0, e pertanto la nozione di separabilità è veramente significativa solo in caratteristica p. Un ampliamento algebrico L di K è separabile su K se ogni elemento di L è separabile su K. (Vi è un modo più generale di definire la separabilità, applicabile ad un ampliamento non necessariamente algebrico).

Ritorniamo ora ad un'algebra A con radicale N su un corpo F. Ricordiamo che A/N è una somma diretta di algebre semplici, i cui centri sono corpi, ampliamenti di F; la separabilità di A/N significa che ciascuno di questi ampliamenti di F è separabile. Allora, se F è algebricamente chiuso o ha caratteristica 0, il teorema principale di Wedderburn non richiede ipotesi aggiuntive.

Il teorema principale di Wedderburn sarà presentato nel cap. 17 sull'algebra omologica da un punto di vista differente.

Così appariva essenzialmente la teoria degli anelli associativi dal 1905 al 1945 circa; vi era in più una osservazione significativa fatta nel 1927 da Artin (ribadita nel 1939 da Hopkins): l'ipotesi della dimensione finita sul corpo poteva essere indebolita presupponendo la condizione della catena discendente sugli ideali unilateri (a sinistra, per fissare le idee). Tali anelli vennero poi chiamati artiniani in onore di Artin.

Nella metà degli anni quaranta, i tempi erano maturi per una teoria degli anelli associativi senza alcuna ipotesi di finitezza. Vari studi di classi speciali di anelli avevano preparato la strada: quelli di Stone sugli anelli di Boole, quelli compiuti da von Neumann sugli anelli ‛regolari' nel suo lavoro sulle geometrie continue, e quelli di Gelfand su quelle algebre che furono poi chiamate algebre di Banach. Dopo significativi lavori di Chevalley (non pubblicati), di Azumaya e Nokayama, di Perlis e di Hille e Zorn, i ‛risultati completi furono pubblicati in una serie di articoli di Jacobson.

Vi è anzitutto una definizione generale di radicale di un anello come intersezione degli ideali sinistri massimali; l'intersezione degli ideali destri massimali è esattamente uguale (sicché, in particolare, il radicale è un ideale bilatero). In un anello artiniano, il radicale di Jacobson coincide con quello di Wedderburn: è l'ideale nilpotente massimale. Se il radicale è nullo, l'anello si dice semisemplice.

La nozione successiva è quella di anello primitivo: un anello che possiede un modulo irriducibile fedele. (Un modulo A è irriducibile - detto anche semplice - se i suoi soli sottomoduli sono O e A. Un modulo è fedele se O è l'unico elemento dell'anello che annulla l'intero modulo). Il concetto di primitività non gode della simmetria sinistra- destra, come mostra un esempio di George Bergman (1964); pertanto con il termine primitivo intenderemo ‛primitivo a sinistra' (cioè che possiede un modulo a sinistra irriducibile e fedele). Un ideale I in un anello A è primitivo se l'anello A/I è primitivo. Teorema: in un anello semisemplice l'intersezione degli ideali primitivi è 0. Questa è la migliore approssimazione, che ci si può aspettare in generale, alla somma diretta artiniana di anelli semplici.

Il teorema di densità di Chevalley-Jacobson descrive la struttura degli anelli primitivi: un anello primitivo A è un anello denso di trasformazioni lineari di uno spazio vettoriale su un corpo. Qui ‛denso' significa che, per ogni n, si ha la n-transitività, cioè n vettori linearmente indipendenti qualsiasi possono essere mandati da un opportuno elemento di A in n immagini arbitrarie; la condizione suddetta è equivalente alla densità topologica in una topologia appropriata. Se A è artiniano, lo spazio vettoriale ha dimensione finita, A consiste di tutte le sue trasformazioni lineari, e riotteniamo il teorema di Wedderburn; in particolare, in tal caso, ‛semplice' e ‛primitivo' coincidono.

Questa teoria di Jacobson ha dimostrato la sua utilità in moltissime applicazioni. Accenniamo a tre di esse.

1. Teoremi di commutatività. Il prototipo di questi teoremi è quello di Stone (1936): un anello di Boole (un anello in cui ogni elemento a soddisfa la condizione a² = a) è necessariamente commutativo. Questo teorema ebbe successive generalizzazioni, che raggiungono il culmine nel seguente enunciato (Herstein, 1953): se, per ogni a, esiste un polinomio p_a con coefficienti interi tale che a²p(a) + a è centrale, allora l'anello è commutativo.

2. Le algebre algebriche metriche complete sono di grado limitato. Mazur congetturò questo risultato (1938) e Kaplansky lo dimostrò (1947) usando essenzialmente un suggerimento di Arens. (Chiarimenti: un'algebra su un corpo F è algebrica se ogni suo elemento soddisfa una equazione algebrica a coefficienti in F; è di grado limitato se l'insieme dei gradi dei polinomi usati è limitato. La frase ‛algebra metrica completa' significa che nell'algebra esiste una struttura di spazio metrico completo, compatibile con le operazioni di algebra).

3. Finitezza locale delle algebre algebriche P. I. In analogia al problema di Burnside sui gruppi, Kurosh nel 1941 pose la questione se un'algebra algebrica con un numero finito di generatori abbia dimensione finita. Se diciamo che un'algebra è localmente finita quando ogni sua sottoalgebra con un numero finito di generatori ha dimensione finita, possiamo riformulare la questione come segue: un'algebra omologica è localmente finita? Nel 1964, Golod rispose negativamente, come si è già detto nel cap. 4 e diremo ancora in seguito; ma la risposta diventa affermativa in presenza di una identità polinomia (P. I.), che definiamo nel capoverso successivo. Dopo risultati importanti, ma parziali, dovuti a Jacobson e a Levitzki, Kaplansky trovò nel 1950 quale è il risultato affermativo più forte che si possa ottenere nel problema di Kurosh.

Diciamo che un'algebra A su F soddisfa una identità polinomia se esiste un polinomio non nullo f (con coefficienti in F) nelle variabili non permutabili x₁, x₂, ..., x_n tale che f(a₁, ..., a_n) = 0 per tutte le a_i in A. L'esistenza di identità interessanti di questo tipo segue dall'osservazione che un'algebra di dimensione m soddisfa l'identità del tipo

dove la somma è fatta su tutte le permutazioni π e il segno è + o − a seconda che π sia pari o dispari. L'algebra di tutte le matrici r × r ha dimensione r² e pertanto soddisfa l'identità (detta ‛standard') scritta sopra in r² + 1 variabili. Amitsur e Levitzki dimostrarono (1950) che, in questo caso, r² + 1 può essere abbassato a 2r e si vede facilmente che 2r è il miglior risultato possibile.

Per le matrici 2 × 2 su un campo ed anche per i corpi di quaternioni su F (cioè algebre con divisione di dimensione 4 su F ed il cui centro è F) si ha la seguente identità, ricavata per la prima volta da Marshall-Hall (1943):

(xy − yx)²z − z(xy − yx)² = 0.

Questa identità si può esprimere dicendo che (xy − yx)² (il quadrato di un commutatore additivo) sta sempre nel centro. ‛ un fatto, inoltre, che (xy − yx)² non è sempre zero.

Il problema di sapere se matrici di ordine maggiore ammettessero polinomi centrali rimase insoluto fino al 1972, quando Formanek scoprì un metodo per costruire polinomi siffatti. Tale metodo è abbastanza semplice da poter essere qui riportato. limitandoci, per semplicità, al caso n = 3. Sia f il polinomio in quattro indeterminate permutabili

f = (x₁ − x₂)(x₄ − x₂)(x₁ − x₃)(x₄ − x₈)(x₂ − x₈)².

Ad f associamo un polinomio F(X, Y₁, Y_2, Y₃) in quattro indeterminate, non permutabili, di grado 6 in X e multilineare nelle Y_i. L'idea è di associare ad x₁, x₂, ..., x₄ i posti tra Y₁, Y₂, Y₃, inclusi il posto finale e quello iniziale; esplicitamente, al monomio xr₁¹xr₂²xr₃³xr₄⁴ associamo il monomio X^r1Y₁X^r2Y₂X^r3Y₃X^r4. Allora

F(X, Y₁, Y₂, Y₃) + F(X, Y₂, Y₃, Y₁) + F(X, Y₃, Y₁, Y₂)

è un polinomio centrale del tipo desiderato, come si verifica senza soverchie difficoltà, dal momento che è sufficiente prendere la matrice X diagonale e tutte le matrici Y unità.

I polinomi centrali di Formanek promettono di essere utili in certe questioni riguardanti anelli che soddisfano una identità polinomia. Sembra ragionevole predire che la teoria degli anelli P. I. raggiungerà tra non molto pressappoco lo stesso livello della teoria degli anelli commutativi in generale.

Torniamo ora da questa digressione sui polinomi centrali al problema di Kurosh della finitezza locale delle algebre algebriche. Come si è osservato dianzi e nel cap. 4, la questione generale ebbe una risposta negativa nel 1964 da Golod, che costruì un'algebra, generata da due elementi, che era nil eppure di dimensione infinita. Tale costruzione era valida su un corpo arbitrario (più precisamente, valida dapprima su un corpo numerabile, fu estesa poi, con un artificio, ai corpi non numerabili). Se il corpo ha caratteristica p ≠ 0, si può fare una connessione con il problema di Burnside, che descriveremo con l'aiuto di un elemento unità formale (ciò può essere evitato ricorrendo alla operazione ‛circolare': xoy = x + y + xy). Per ogni elemento a nell'algebra, si ha (1 + a)^pr = 1, per una conveniente potenza p^r di p, poiché a è nilpotente; gli elementi 1 + a, al variare di a nell'algebra, formano un gruppo di torsione, di fatto un p-gruppo, che non è localmente finito. Certamente l'interesse per questo controesempio al problema illimitato di Burnside è diminuito dopo la pubblicazione della risposta negativa di Adyan e Novikov al problema limitato di Burnside.

Restano ancora aperte alcune questioni, in certo qual modo analoghe al problema di Kurosh, tra le quali emerge la seguente, proposta da Köthe: un ideale unilatero nil genera un ideale bilatero nil?

Concludendo questo capitolo, accenniamo ad un altro argomento. La definizione di Jacobson di radicale di un anello portò al concetto di anello radicale (un modo ‛complicato di definire un anello radicale è che l'anello sia un gruppo rispetto all'operazione circolare x + y + xy). Sorge allora la questione: esistono anelli radicali semplici? Un tale anello fu costruito da Sasiada nel 1961 e un'esposizione rifinita fu pubblicata nel 1967 da Sasiada e Cohn. Ancora aperta è la questione parallela: esistono anelli nilpotenti semplici?

Il trattato di Jacobson (v., 1964) è l'opera definitiva sugli anelli associativi.

11. Anelli di gruppo e rappresentazioni di gruppi

Iniziamo questo capitolo con la definizione di anello di gruppo RG di un gruppo G su un anello commutativo R: esso consiste di tutte le espressioni Σ a_ig_i con a_i in R e g_i in G, le operazioni di addizione e moltiplicazione sono quelle ovvie. (Facciamo due osservazioni sulle generalizzazioni. Non occorre che l'anello R sia commutativo; si è preso R commutativo perché i casi che verranno considerati qui sono quelli in cui R è un corpo o è l'anello degli interi. Inoltre si può prendere per G un semigruppo, cioè un insieme con una legge binaria associativa; comunque, è preferibile supporre che G sia dotato di un elemento unità, poiché, in tal caso, si ha un elemento unità anche in RG. Un semigruppo con unità è detto anche un monoide).

Possiamo considerare gli anelli di gruppo come ricche sorgenti di esempi: da ogni gruppo G e da ogni anello di coefficienti R si ottiene un nuovo anello RG. Ma la loro importanza fondamentale sta nel fatto che essi costituiscono un legame tra la teoria dei gruppi e quella degli anelli, il che apre una nuova prospettiva nello studio dei gruppi. Ciò accade, soprattutto, perché vi è un legame corrispondente tra moduli su gruppi e moduli su anelli. Infatti, con l'ovvia definizione di G-modulo (o rappresentazione di G) come un R-modulo su cui opera G, vi è una corrispondenza biunivoca tra G-moduli e RG-moduli.

È naturale chiedersi in quali casi la teoria dei moduli su un dato anello si comporti ‛particolarmente bene'. La cosa più desiderabile è che ogni modulo sia somma diretta di moduli irriducibili. A questo punto enunciamo un teorema, che abbiamo omesso dal nostro panorama sugli anelli, posponendolo fino ad ora: un anello ha la proprietà che tutti i suoi moduli sono somme dirette di moduli irriducibili se, e solo se, è semisemplice artiniano.

Se R è un corpo (chiamiamolo F) e G è un gruppo finito, allora FG è un'algebra di dimensione finita su F. Quando è che essa è semisemplice? La risposta è data da un teorema di Maschke (1899), aggiornato in modo da valere per tutti i corpi possibili. Se F ha caratteristica p ≠ 0, F è semisemplice se, e solo se, l'ordine di G è primo rispetto a p. Il caso in cui l'ordine di G è divisibile per p è stato studiato a fondo da Brauer e dalla sua scuola. La teoria dei ‛caratteri modulari' che ne risulta fornisce i fondamenti per la costruzione dei ‛caratteri ordinari' che sono quelli ottenuti sul corpo dei numeri complessi (daremo tra poco la definizione del termine ‛carattere'). Non daremo qui ulteriori informazioni sull'argomento, che è molto specialistico.

Nel caso semisemplice, per i nostri propositi possiamo prendere come corpo F quello dei numeri complessi. La teoria dei moduli su un anello artiniano semisemplice A rivela che gli A-moduli irriducibili sono in corrispondenza biunivoca con le parti semplici che costituiscono A. Ritornando a FG, osserviamo che ogni sua parte semplice è l'algebra di tutte le matrici r_i × r_i su F, per un certo intero r_i, che è detto il grado della corrispondente rappresentazione irriducibile di G. Osserviamo inoltre che una delle r_i è uguale a 1, perché abbiamo la rappresentazione banale di G, che applica ogni elemento nella matrice identità 1 × 1. Vale ovviamente l'equazione Σ r2_i = n, dove n è l'ordine di G. Già più profondo è il fatto notevole secondo cui ogni r_i divide n. Il caso in cui G è abeliano non presenta alcun interesse, in quanto tutte le r_i (e sono n) sono uguali ad 1. Il primo esempio non commutativo è offerto dal gruppo di ordine 6, S₃, o gruppo simmetrico su tre oggetti. Vi sono due rappresentazioni di dimensione 1, che sono in realtà rappresentazioni del gruppo quoziente S₃/A₃, e due rappresentazioni irriducibili di dimensione 2. L'identità 6 = 1² + 1² + 2² offre una verifica delle affermazioni precedenti.

Più della rappresentazione stessa, è invariante la funzione che si ottiene assegnando ad ogni elemento del gruppo la traccia della matrice che lo rappresenta (la traccia di una matrice è la somma di tutti gli elementi della diagonale principale). Tale funzione è detta ‛carattere' e, se la rappresentazione è irriducibile, ‛carattere irriducibile'. Notiamo che, a differenza della rappresentazione stessa, il carattere della rappresentazione è indipendente dalla scelta della base nello spazio vettoriale su cui la rappresentazione opera. Inoltre, un carattere è in realtà una funzione sulle classi coniugate del gruppo (due elementi a, b in un gruppo sono coniugati se esiste un elemento x per cui x^-1 ax = b; una classe coniugata consiste di tutti gli elementi coniugati ad un elemento dato), e il numero dei caratteri irriducibili (e quindi il numero delle rappresentazioni irriducibili) è uguale al numero delle classi coniugate. I caratteri soddisfano certe relazioni di ortogonalità. Tutte queste informazioni sommate insieme sono di grande aiuto nella costruzione della tavola dei caratteri del gruppo.

È accaduto più di una volta che, nel ricercare un gruppo sporadico semplice, fosse già disponibile, almeno in parte, la tavola dei caratteri, prima ancora di sapere se questo gruppo fantasma esistesse effettivamente.

La nostra esposizione delle rappresentazioni di un gruppo termina qui (ulteriori notizie potranno trovarsi nell'articolo gruppi). Aggiungiamo solo che le rappresentazioni dei gruppi finiti sono largamente usate in fisica, ed hanno di fatto un ruolo vitale nella meccanica quantistica. Molto usate sono anche le rappresentazioni dei gruppi di Lie, cosicché il contenuto del cap. 15 è pertinente alla fisica.

Aggiungiamo ancora qualcosa sugli anelli di gruppi infiniti, nel caso in cui l'anello dei coefficienti sia un corpo F. Mentre, come si è notato dianzi, le algebre FG costituiscono una ricca sorgente di esempi, le applicazioni della teoria degli anelli alla teoria dei gruppi, nel caso in cui G è infinito, partendo da FG, non hanno ancora raggiunto un livello significativo.

Vi sono comunque alcuni interrogativi interessanti, fra i quali vogliamo citare il seguente: se F ha caratteristica 0, FG è semisemplice? Il lavoro di Amitsur ha fatto fare progressi notevoli alla soluzione di questo problema; per esempio, si sa che la risposta è affermativa se F non è algebrico sui numeri razionali.

Molte applicazioni ha avuto l'anello di gruppo ZG di G sull'anello Z degli interi, di cui ci occuperemo nel cap. 17, dedicato all'algebra omologica.

Il libro di Passman (v., 1971) è una ampia monografia sugli anelli di gruppo di gruppi infiniti.

12. Anelli non associativi in generale

A questo capitolo introduttivo, ne seguiranno altri tre sugli anelli non associativi, uno per ogni classe (alternativi, di Jordan e di Lie) che, come si è detto nel cap. 7, comprendono tutti gli anelli non associativi che meritano di essere studiati a fondo. Se non si pone alcuna condizione al posto della legge associativa, non c'è quasi nulla da dire; pertanto sono state prese in considerazione svariate leggi sostitutive. Cominciamo con l'osservare che la legge commutativa per se stessa dà ben poco.

Senza l'associatività, la formulazione dei concetti fondamentali può essere laboriosa. Per esempio, la condizione di nilpotenza diventa ambigua. Il significato del simbolo aⁿ diviene univoco se si suppone che la legge associativa sia valida per le potenze di a, condizione, questa, chiamata ‛associatività delle potenze' da Albert, che la introdusse nel 1948. Egli dimostrò che, eccetto che per alcuni valori piccoli della caratteristica, l'associatività delle terze e quarte potenze implica quella di tutte le altre. Per tutti gli anelli che prenderemo qui in considerazione presupporremo l'associatività delle potenze, eccetto che per le algebre reali con divisione, di cui parliamo qui di seguito.

Ricordiamo che, nel corpo dei numeri reali, si hanno le seguenti ben note algebre con divisione: i numeri reali stessi, i numeri complessi, i quaternioni ed i numeri di Cayley. Le loro dimensioni sono rispettivamente 1, 2, 4 e 8. Sono queste le sole possibilità per la dimensione di un'algebra con divisione sui numeri reali? Limitandosi a considerazioni di natura puramente algebrica non si riuscì a risolvere questo problema. La risposta, che dobbiamo ai topologi, è che non è possibile alcun altro valore per la dimensione. Il passo conclusivo nella dimostrazione fu compiuto da Kervaire nel 1958 e, indipendentemente e pressoché simultaneamente, da Milnor. Il teorema topologico, che essi dimostrarono, stabilisce che la sfera n-dimensionale è ‛parallelizzabile' se, e solo se, n = 1,3 o 7.

13. Anelli alternativi

Come si è osservato precedentemente (v. cap. 9), in relazione al prodotto di somme di quadrati, Cayley scoprì un'algebra di dimensione 8, sul corpo dei numeri reali, che gli fornì una formula per moltiplicare somme di 8 quadrati. Invece di occuparci di quest'algebra ne prendiamo qui in considerazione un'altra, molto vicina ad essa, che è più facile a descriversi e, in un certo senso, più importante.

Artin mise in luce una proprietà chiave dell'algebra di Cayley, che può essere formulata come segue: il sottoanello generato da due suoi elementi qualsiasi è associativo; inoltre, Artin dimostrò che per garantire tale proprietà basta che siano soddisfatte le due identità: a(ab) = a²b e (ba)a = ba². Tali identità vengono perciò assunte come assiomi per definire la struttura di ‛anello alternativo'. Il nome deriva da un'altra versione equivalente della definizione, secondo cui l'‛associatore' (a, b, c) = (ab)c − a(bc) è una funzione alternante dei suoi argomenti.

Zorn (1930) lavorò sulla teoria di struttura delle algebre alternative di dimensione finita e trovò che si poteva generalizzare perfettamente la teoria di Wedderburn, e che l'unica novità era la presenza di altre algebre semplici. Su un corpo algebricamente chiuso vi è infatti esattamente una nuova algebra semplice; essa ha dimensione 8 ed è detta l'algebra delle matrici di Cayley. Un modo di descriverla può essere il seguente: siano V e W due spazi vettoriali di dimensione 3 su un dato corpo F, e sia C l'insieme di tutte le ‛matrici'

con a e b in F, x in V e y in W. Queste matrici vengono moltiplicate in modo pressoché naturale, ma sono necessarie due avvertenze: quando x moltiplica y si usa il prodotto scalare di questi vettori tridimensionali; inoltre, diventa inevitabile l'introduzione dei seguenti due tipi speciali di prodotto:

dove × denota il prodotto vettoriale.

Con tali regole per il prodotto, C è l'algebra delle matrici di Cayley su F.

Su un corpo qualsiasi si hanno anche le algebre di Cayley con divisione: algebre con divisione di dimensione 8 che diventano algebre di matrici di Cayley quando il corpo di base viene esteso fino a divenire algebricamente chiuso; per esempio, sul corpo dei numeri reali vi è una sola algebra con divisione di Cayley, quella scoperta da Cayley.

Se si rinuncia all'ipotesi che la dimensione sia finita, si perviene ad un risultato molto netto per gli anelli alternativi semplici. Tale risultato − che era stato ottenuto in un primo tempo da Bruck e Kleinfeld (1951) per i corpi, e fu poi esteso da Kleinfeld, in una serie di tappe successive, agli anelli semplici - può essere formulato come segue: un anello alternativo semplice è associativo oppure è un'algebra con divisione di Cayley o, infine, un'algebra di matrici di Cayley.

14. Anelli di Jordan

Gli anelli di Jordan si ottengono introducendo negli anelli associativi un'operazione nuova: a∘b =ab + ba. Si perde, in tal modo, l'associatività, guadagnando la commutatività, che però ne è un debole sostituto. Tuttavia, come si verifica direttamente, vi è una identità di quarto grado di tipo associativo:

(a²∘b)∘a = a²∘(b∘a).

Un anello commutativo che soddisfi tale identità, si chiama ‛anello di Jordan'. L'idea di definire questo tipo di struttura ebbe origine nel' 1934 in un articolo di Jordan, von Neumann e Wigner, in vista di eventuali applicazioni alla meccanica quantistica. Tali applicazioni non si realizzarono, almeno non nel modo previsto dagli autori, ma gli anelli di Jordan divennero un tema di studi importanti dell'algebra moderna, e la loro connessione con la teoria delle funzioni di più variabili complesse diede loro una nuova dimensione.

Jordan, von Neumann e Wigner supponevano di avere come dato di partenza un'algebra di Jordan di dimensione finita sul corpo dei numeri reali, soddisfacente una certa condizione formale di realtà, che precludeva la presenza di qualsiasi cosa che assomigliasse ad un radicale. Infatti, risultò che l'algebra in questione era una somma diretta di algebre semplici. Come descriveremo in seguito, in un contesto più generale, risultò inoltre che le algebre semplici erano le algebre usuali, con una sola eccezione. Questa algebra eccezionale (che essi denominarono M₈³) aveva dimensione 27 ed era descrivibile come l'algebra di tutte le matrici hermitiane 3 × 3 sull'algebra reale con divisione di Cayley.

Chiamiamo ‛speciale' un anello di Jordan che sia isomorfo ad un sottoanello (di Jordan) di un anello ottenuto da uno associativo usando il prodotto ab + ba. Sorge immediatamente una questione: M₈³ è speciale? Ad essa fu data subito una risposta negativa da Albert (1934).

Restava ancora una questione più difficile: M₈³ può essere immagine omomorfa di un anello di Jordan speciale? O, equivalentemente, ogni anello di Jordan è immagine omomorfa di un anello di Jordan speciale? La risposta continua ad essere negativa, come fu, mostrato più tardi da Albert e Paige (1959). Poiché ciò è equivalente a chiedersi se vi sono delle identità soddisfatte da anelli di Jordan speciali, ma non da tutti gli anelli di Jordan, Albert e Paige dimostrarono l'esistenza di tali identità: ma il loro metodo non era abbastanza costruttivo da fornirne esplicitamente una. Sette anni più tardi, Glennie (1966) ne costruì molte. Presentiamo qui una di esse, usando l'abbreviazione:

{a, b, c} = a(bc) − b(ca) + c(ab)

dove a destra il prodotto di Jordan è indicato semplicemente per giustapposizione di simboli, come nell'identità stessa. L'identità di Glennie:

2{xzx}{y{zy²z}x} − 2{yzy} {x{zx²z}y} −

−{x{z{x{yzy}y}z}x} + {y{z{y{xzx}x}z}y} = 0

è soddisfatta negli anelli di Jordan speciali (come si verifica facilmente in modo automatico), ma non in M8³.

Concludendo, descriveremo la struttura delle algebre di Jordan di dimensione finita (escludendo il caso di caratteristica 2, che è ben differente). Essa è dovuta ad Albert, eccetto per un punto finale stabilito da Jacobson. L'impostazione generale è sostanzialmente quella di Wedderburn. Il radicale è l'ideale nilpotente massimale e le algebre semi- semplici sono somme dirette di quelle semplici. Mettendo da parte le generalizzazioni di M8³ (chiamate algebre di Jordan semplici eccezionali) e certe altre algebre piuttosto banali costruite a partire da forme quadratiche, restano due classi di anelli che possiamo descrivere senza ipotesi di finitezza per la dimensione. La loro semplicità fu dimostrata da Herstein (1955-1956): 1) prendiamo un arbitrario anello associativo semplice e usiamo l'operazione ab + ba; 2) in un anello associativo semplice con involuzione*, prendiamo gli elementi simmetrici (cioè quelli che soddisfano la condizione x* = x) nell'operazione ab + ba. In entrambi i casi si ottiene un anello di Jordan semplice.

Il libro di Jacobson (v., 1968) è un ampio trattato sulle algebre di Jordan.

15. Anelli di Lie

Incominciamo ad occuparci degli anelli di Lie in modo parallelo a quello seguito all'inizio del capitolo precedente. Dato un anello associativo arbitrario A, introduciamo in esso una nuova operazione: il commutatore [ab] = ab-ba. Ovviamente, essa soddisfa la condizione di anti-commutatività [ab] = − [ba] e - come si verifica facilmente - la identità di Jacobi:

[[ab]c] + [[bc]a] + [[ca]b] = 0.

Queste due identità sono gli assiomi che definiscono un anello di Lie.

Questa presentazione non segue affatto lo sviluppo storico. Gli anelli di Lie nacquero in connessione con lo studio dei gruppi chiamati ‛gruppi continui' da Lie e, più tardi, ‛gruppi di Lie'. Come già si è detto nel cap. 3, un gruppo di Lie è un gruppo topologico in cui esiste un intorno dell'identità identificabile con un aperto di uno spazio euclideo, in modo tale che le operazioni di gruppo siano funzioni analitiche. Ad un tale gruppo viene associata una algebra di Lie di dimensione finita sul corpo dei numeri reali, la quale non determina completamente il gruppo, ma si avvicina molto a determinarlo; più esattamente, essa caratterizza il gruppo ‛localmente'. Se supponiamo che il gruppo si comporti localmente come uno spazio vettoriale complesso e che le operazioni di gruppo siano funzioni complesse analitiche, otteniamo un'algebra di Lie complessa. L'antico nome di ‛gruppo infinitesimale' fu molto più tardi sostituito da quello di ‛algebra di Lie' per suggerimento di Weyl.

Poniamoci ora la stessa domanda che ci siamo posti per gli anelli di Jordan: può ogni anello di Lie essere ottenuto come sottoanello di Lie di un conveniente anello associativo con l'operazione di commutazione? Qui la risposta è affermativa senza riserve, come fu anticipato da Poincaré ed in seguito stabilito indipendentemente da Birkhoff e da Witt. Una questione parallela, alla quale è importante dare risposta, è se il risultato precedente continui a sussistere quando si richiede che le algebre siano tutte di dimensione finita. In altre parole, un'algebra di Lie di dimensione finita può essere ottenuta partendo da un'algebra associativa di dimensione finita, sostituendone la moltiplicazione con la commutazione e passando poi ad una sua sottoalgebra di Lie? Ado (1947) e Iwasawa (1948) dimostrarono, rispettivamente nel caso di caratteristica O e in quello di caratteristica p, che la risposta è affermativa. È interessante notare che questa è una delle rare situazioni in cui la caratteristica p richiede una dimostrazione differente, e più facile, rispetto a quella in caratteristica O.

Una teoria della struttura delle algebre di Lie di dimensione finita (su un corpo algebricamente chiuso) è stata completata solo in caratteristica O (in caratteristica p è ancora frammentaria e non diremo più nulla in proposito); essa è dovuta a Killing e Cartan. Come si è già osservato all'inizio del cap. 10, la teoria delle algebre di Lie precedette quella più semplice delle algebre associative. Poiché essa è rimasta essenzialmente la stessa fino ai giorni nostri, sarebbe improprio, anche se vero, dire che essa segue l'impostazione di Wedderburn. Ad ogni modo, vi compare un radicale, che è però qualcosa di più grande dell'ideale nilpotente massimale; l'ideale risolubile massimale è la scelta giusta. (Un'algebra generica A è risolubile se la serie A, A², (A²)², ... ottenuta elevando successivamente al quadrato, raggiunge lo zero dopo un numero finito di passi. La nozione non ha interesse nelle algebre alternative o di Jordan, perché coincide allora con la nilpotenza). Il nome ‛risolubile' deriva dal fatto che un gruppo di Lie connesso è risolubile (nel senso usuale della teoria dei gruppi) se, e solo se, la sua algebra di Lie è risolubile. Come sempre, le algebre di Lie semisemplici sono somme dirette di algebre semplici.

Il passo successivo è quello di supporre che il corpo di base sia algebricamente chiuso ed elencare le algebre di Lie semplici; ve ne sono cinque ‛sporadiche' e varie famiglie infinite di ‛normali' (di solito si usa il termine ‛eccezionali' più che ‛sporadiche', e comunque i gruppi semplici finiti corrispondenti alle algebre di Lie eccezionali semplici non sono da considerarsi sporadici, in quanto appartengono a famiglie infinite ben determinate). Torneremo in seguito sulle algebre eccezionali; prima descriviamo quelle normali così come si è fatto per le analoghe algebre di Jordan, comprendendo anche certe algebre di dimensione infinita.

Escludiamo di nuovo il caso in cui il corpo base abbia caratteristica 2. Sia A un anello associativo semplice e Z sia il suo centro (Z è O oppure è un corpo). Allora [A A]/(Z ⋂ [A A]) è un anello di Lie semplice. Sia B un anello semplice con un'involuzione*, e sia K l'insieme degli elementi antisimmetrici di B (cioè soddisfacenti la x* = − x). Allora [K K]/(Z ⋂ [K K]) è un anello di Lie semplice, se scartiamo alcune eccezioni che si presentano per piccole dimensioni. Questi risultati sono dovuti a Herstein e Baxter (1955-1958). Le versioni di dimensione finita di queste algebre (su un corpo algebricamente chiuso di caratteristica O), furono indicate con A_n, B_n, C_n, e D_n da Killing e Cartan. Come si è già accennato, essi trovarono esattamente 5 algebre in più: G_2, F₄, E₆, E₇, E₈. (Questa terminologia corrisponde all'identificazione delle algebre mediante certi diagrammi di ^tradici', la cui descrizione occuperebbe troppo spazio). Successivamente si notarono delle connessioni con le algebre alternative e di Jordan. Così, G₂ è l'algebra delle derivazioni dei numeri di Cayley, F₄ è l'algebra delle derivazioni dell'algebra di Jordan eccezionale. Una derivazione D di un anello è una applicazione additiva che soddisfa la legge della derivata del prodotto: D(xy) = (Dx)y + x(Dy). Le derivazioni di un anello formano un anello di Lie per la commutazione. E₆, E₇, E₈ ammettono identificazioni analoghe, ma più complicate.

Le rappresentazioni delle algebre di Lie sono significative soprattutto perché connesse intimamente con le rappresentazioni dei gruppi di Lie. Una rappresentazione di un'algebra di Lie L su un corpo F è un omomorfismo di Lie da L alle trasformazioni lineari di uno spazio vettoriale su F. Qui il risultato rilevante è che ogni rappresentazione di un'algebra di Lie semisemplice è completamente riducibile (naturalmente si assume che la caratteristica sia O); esso fu ottenuto prima da Weyl (1925), che proiettò il problema sui gruppi compatti che offrono la possibilità di integrazione (Weyl lo chiamò ‛il trucco unitario'). Più tardi, Whitehead (1936) diede una dimostrazione puramente algebrica di questo teorema e del teorema di Levi, analogo a quello principale di Wedderburn (v. cap. 10), dimostrando due lemmi tecnici estremamente interessanti. Torneremo sull'argomento nel cap. 17 dedicato all'algebra omologica.

L'opera conclusiva sulle algebre di Lie è il libro di Jacobson (v., 1962).

16. Anelli commutativi

In questo capitolo prenderemo in considerazione anelli commutativi e associativi. Avremmo dovuto trattare questi anelli nel cap. 10, ma in quel capitolo abbiamo dedicato la massima attenzione alle algebre di dimensione finita ed alle loro generalizzazioni, gli anelli artiniani; mentre il caso artiniano ha qui un interesse piuttosto marginale.

La teoria degli anelli commutativi ha due fonti principali: una è la teoria dei numeri algebrici che, iniziata con Gauss, fu plasmata ad opera di Kummer, Dedekind, Dirichlet e Kronecker e raggiunse livelli elevatissimi con Hilbert. L'altra è la geometria algebrica, sviluppata da molti matematici tedeschi ed italiani. La più importante di queste due motivazioni è la seconda, in quanto si può dire che, mentre la teoria dei numeri algebrici riguarda il caso di dimensione I e gli anelli artiniani quello di dimensione O, la geometria algebrica rappresenta il caso generale.

Poiché i numeri algebrici e la geometria algebrica non rientrano nel quadro generale delineato in questo articolo, ci occuperemo della teoria degli anelli commutativi come di una disciplina autosufficiente e ci volgeremo solo occasionalmente alle origini storiche.

La teoria degli anelli commutativi è dominata dal concetto di ideale primo; un ideale I in un anello commutativo R è primo se, ogniqualvolta un prodotto ab è in I, o a o b appartiene a I. In altri termini possiamo dire che I è primo se R/I è un campo d'integrità (non ha divisori dello zero). In un anello non commutativo il modo proprio di generalizzare la nozione di ideale primo è di supporre che aRb ⊂ I implichi che a o b è in I. Naturalmente potevamo anche copiare semplicemente la definizione del caso commutativo e dire che I è primo se ab ∈ I implica che a o b è in I, ma tale proprietà è troppo raramente soddisfatta per essere utile. Per quanto vi siano anche numerosi risultati sugli ideali primi di anelli non commutativi, in questo capitolo ci occuperemo soltanto del caso commutativo. Da ora in poi, in questo capitolo, ‛anello' va inteso come ‛anello commutativo'.

Indichiamo ora sommariamente in qual modo gli anelli commutativi nascano dalla geometria algebrica, e come in essa si inquadrino gli ideali primi. In geometria algebrica, si lavora con equazioni algebriche nelle variabili x₁, x₂, ..., x_n su un dato corpo k algebricamente chiuso (nel caso classico, il corpo dei numeri complessi). Una varietà V è l'insieme di tutti i punti che soddisfano una famiglia di equazioni algebriche. Una varietà è, in modo essenzialmente unico, unione di un numero finito di varietà che sono irriducibili, nel senso che non possono essere decomposte in altre varietà. Sia V una varietà irriducibile e sia P l'insieme di tutti i polinomi che si annullano su V. Allora P è un ideale primo nell'anello k [x₁, . .., x_n] dei polinomi in x₁, ..., x_n con coefficienti in k; in tal modo si ottiene una corrispondenza biunivoca tra le varietà irriducibili e gli ideali primi ed a V corrisponde il campo di integrità k[x₁, ..., x_n]/P. Riassumendo, le varietà sono legate agli ideali primi ed anche ai campi d'integrità con un numero finito di generatori su un corpo.

Osservazione. Si è usato il termine ‛varietà', ma sarebbe stato più esatto parlare di ‛varietà affine'. La geometria algebrica si occupa delle varietà proiettive, ma sono state inventate varietà ancora più generali, che comprendono le varietà affini, quelle proiettive ed altre ancora.

In due lavori (1893 e 1895), diventati classici, Hilbert dimostrò due dei teoremi fondamentali su questo argomento. Il primo asserisce che ogni ideale in k [x₁, ..., x_n] ha un numero finito di generatori, se k è un corpo. L'importanza di quest'ultima condizione fu messa in rilievo da Emmy Noether in un articolo del 1921 e, in seguito a ciò, si chiamarono ‛noetheriani' quegli anelli in cui ogni ideale ha un numero finito di generatori o, equivalentemente, in cui gli ideali soddisfano la condizione della catena ascendente. (Notiamo che, in un certo senso, gli anelli artiniani, dove vale la condizione della catena discendente, sono i duali di quelli noetheriani; ma si tratta di una dualità bizzarra. Nel 1939 Hopkins dimostrò che la condizione della catena discendente implica quella della catena ascendente anche in anelli non commutativi). Oggi, il teorema di Hilbert si enuncia e si dimostra nella forma seguente: se R è noetheriano anche R [x] è noetheriano. Vale la pena di osservare che, in questa forma, la dimostrazione è più agevole; è vero che si ha a che fare con un anello di coefficienti molto generale, ma è un prezzo che si può pagare per ottenere in cambio il vantaggio di lavorare in una sola variabile.

Il secondo teorema fondamentale di Hilbert è il Nullstellensatz, che si può enunciare in numerose forme differenti. Ne abbiamo già dato una versione, senza specificare che fosse il Nulltellensatz, quando abbiamo parlato della corrispondenza biunivoca tra varietà irriducibili ed ideali primi. Ne daremo un'altra formulazione limpida e breve, connessa con il metodo che si usa nell'analisi funzionale per trattare gli anelli di funzioni. Nell'anello k [x₁, ..., x_n] dei polinomi in n variabili su un corpo k algebricamente chiuso, consideriamo l'insieme dei polinomi che si annullano in un punto; esso è un ideale massimale. Il Nullstellensatz asserisce che tutti gli ideali massimali si ottengono in questo modo.

La teoria degli anelli commutativi, nello stile del XX secolo, ebbe inizio nel 1905 da un articolo di Lasker. Egli dimostrò che in k [x₁, ..., x_n] ogni ideale è una intersezione di ideali primari. (Omettiamo la definizione esatta di ideale primario; è sufficiente notare l'analogia del teorema di Lasker con l'espressione di un intero come prodotto di potenze di interi primi). Sedici anni dopo, Emmy Noether dimostrò con un ragionamento breve e molto elegante la proprietà suddetta, quando è soddisfatta la condizione della catena ascendente. Nacque così la teoria degli anelli noetheriani.

Il teorema dell'ideale principale. Sia P un ideale primo in un anello R. Consideriamo tutte le catene di ideali primi discendenti da P. La massima lunghezza di una tale catena ha due nomi nella letteratura: rango e altezza; noi useremo ‛rango'. Il rango può essere infinito, ma un teorema di Krull (1928) dice che nel caso noetheriano il rango è finito. Anzi, è possibile una valutazione accurata: se P è minimale in un ideale generato da n elementi, il rango di P è al più n.

Il massimo dei ranghi di tutti gli ideali primi è la dimensione di Krull di R. La dimensione di Krull sale dai casi più semplici a quelli più interessanti. Per gli anelli noetheriani, se la dimensione di Krull è O siamo nel caso artiniano, se la dimensione di Krull è 1 siamo essenzialmente nel contesto della teoria dei numeri algebrici. In relazione alla geometria algebrica, la dimensione di Krull corrisponde alla dimensione della varietà.

Anelli locali regolari. - Nella terminologia più usata, un anello è quasi locale se ha esattamente un ideale massimale, è locale se in più è noetheriano. Sia R locale, con ideale massimale M e supponiamo che M sia generato da n elementi, con n minimale. Il teorema dell'ideale principale dice che il rango di M è al più n. Il caso di uguaglianza è particolarmente interessante e di esso cominciò ad occuparsi Krull nel 1937. Ora viene usato universalmente per questi anelli l'appellativo di ‛regolari', proposto da Chevalley.

In connessione con la geometria algebrica, ad ogni punto di una varietà si può associare un dominio locale. Zariski (1947) dimostrò che un tale dominio locale geometrico è regolare se, e solo se, il punto non è un punto multiplo della varietà.

Gli anelli locali regolari hanno molte proprietà utili, due delle quali vogliamo ricordare qui: ogni anello locale regolare è un dominio; inoltre, esso è un dominio a fattorizzazione unica (ciò significa che la fattorizzazione di un elemento in elementi che non possono essere ulteriormente fattorizzati è essenzialmente unica). Torneremo su questo secondo punto nel capitolo successivo, dedicato all'algebra omologica.

R-successioni e anelli di Macaulay. - Il concetto di R-successione nacque nella metà degli anni cinquanta ed è quindi abbastanza recente. Tuttavia esso è, in un certo senso, già implicito nel lavoro del matematico britannico Macaulay (specialmente nel suo opuscolo sui sistemi modulari del 1916), che però attrasse ben poca attenzione durante la vita del suo autore. All'inizio le R-successioni erano molto legate all'applicazione, appena sviluppata, dei metodi omologici alla teoria degli anelli commutativi, fino a che nuove dimostrazioni posero la teoria in una condizione autonoma.

Nella nostra esposizione prenderemo in considerazione solo le R-successioni contenute nell'anello, sebbene in una trattazione completa sarebbe preferibile considerare anche R-successioni nei moduli. La successione a₁, a₂, ..., a_n in R è una R-successione se a₁ non è un divisore dello zero, l'immagine di a₃ in R/(a₁) non è un divisore dello zero, l'immagine di a₃ in R/(a₁, a₂) non è un divisore dello zero, e così via. Fissato un ideale I, esaminiamo le R-successioni contenute in I, massimali (la cui esistenza è garantita dalla condizione della catena ascendente). Vale il teorema importante secondo cui tutte le R-successioni massimali contenute in I hanno la stessa lunghezza. Questo invariante è chiamato ‛codimensione' ,‛grado', o ‛profondità' di I.

Un facile teorema afferma che il rango di un ideale primo non è inferiore al grado. Anche qui, come per le considerazioni che hanno portato alla nozione di regolarità di un anello locale, merita speciale attenzione il caso di uguaglianza. Un anello noetheriano si dice di Macaulay se il grado ed il rango di ciascun ideale primo coincidono. Alcuni autori lo chiamano anello di Cohen-Macaulay in onore dell'opera pionieristica di I. S. Cohen (1946) su questi concetti in un anello locale regolare.

Per il loro buon comportamento e per la frequenza con cui si presentano, gli anelli di Macaulay sono diventati uno strumento fondamentale di ricerca. Gli anelli locali regolari sono di Macaulay e gli anelli di Macaulay hanno soddisfacenti proprietà di stabilità; per esempio, se R è di Macaulay anche R[x] e R/(y), dove y non è un divisore dello zero in R, sono di Macaulay. Soprattutto, è esattamente in questi anelli che vale il teorema di Lasker e Macaulay, detto ‛teorema della purezza'.

Concludiamo questo capitolo citando il trattato di Oro- thendieck e Dieudonné (v., 1971), che ha posto nuove basi per la geometria algebrica. Una delle nozioni fondamentali di questa nuova impostazione è quella di ‛schema'. Grosso modo, uno schema è un insieme di anelli commutativi, ‛incollati' l'uno all'altro in modo conveniente; potenzialmente tutto ciò che può dirsi degli anelli commutativi può essere esteso agli schemi. Oltre al loro ruolo in geometria algebrica, gli schemi si sono mostrati utili nell'affrontare questioni riguardanti gli anelli.

Due classici sugli anelli commutativi sono i trattati di Zariski e Samuel (v., 1958 e 1962) e di Nagata (v., 1962).

17. Algebra omologica

La topologia algebrica associa certi invarianti algebrici ad uno spazio topologico X. I più importanti sono: i gruppi di coomologia Hⁿ(X), i gruppi di omologia _n(X) e i gruppi di omotopia π_n(X), che, ad eccezione di π₁(X) (il gruppo fondamentale), sono tutti abeliani.

Essi hanno dei legami tra loro: H₁(X) è identificabile con il gruppo fondamentale, reso abeliano. Un risultato più profondo fu trovato da Hurewicz (1935), quando egli dimostrò che il gruppo fondamentale determina tutti i gruppi di coomologia di dimensione superiore, se si annullano i gruppi di omotopia di dimensione più alta. Eilenberg e MacLane (1943) svilupparono un meccanismo algebrico per esprimere questa dipendenza, provocando cosi, per la prima volta, la proliferazione di metodi topologici in algebra. Essi crearono la teoria della coomologia dei gruppi, inventando i gruppi di coomologia Hⁿ(G, A), dove n è un dato intero, G un gruppo e A un G-modulo. Nell'applicazione topologica citata dianzi, G è π₁(X) e A è il gruppo additivo degli interi, su cui G agisce banalmente.

Ben presto l'algebra fu invasa dai nuovi metodi su due altri fronti: la coomologia delle algebre associative (Hochschild, 1945) e la coomologia delle algebre di Lie (Chevalley ed Eilenberg, 1948). Fra le altre cose, si acquistò una nuova visione di certi vecchi teoremi, che furono poi inseriti in famiglie generali di proposizioni. Per esempio, il teorema principale di Wedderburn per le algebre associative (v. cap. 10) equivale all'asserzione che il secondo gruppo di coomologia di Hochschild si annulla per un'algebra separabile (in effetti, tutti i gruppi di coomologia si annullano). Analogamente, i lemmi di Whitehead sulle algebre di Lie (v. cap. 15) sono i primi due casi dell'enunciato secondo cui tutti i gruppi di coomologia si annullano su un'algebra di Lie semisemplice. La coomologia di gruppi gettò una nuova luce su lavori precedenti, quali l'estensione di gruppi (Schreier, 1926), le rappresentazioni proiettive (Schur, 1904) e la teoria di Galois delle algebre (Teichmüller, 1940).

Dieci anni dopo, Cartan ed Eilenberg unificarono queste tre teorie, e coprirono un campo addirittura più vasto, in un libro importante e di grande risonanza, dove introdussero due strumenti generali: Ext e Tor (v. Cartan e Eilenberg, 1956).

Ext. Sia R un anello e siano A e B due R-moduli a sinistra. Essi definirono dei gruppi abeliani Extn_R(A, B) per n 0, 1, 2, ... . Ext0_R(A, B) coincide con Hom_R(A, B), gruppo degli R-omomorfismi da A a B.

Tor. Sia A un R-modulo a destra e B un R-modulo a sinistra. Essi introdussero anche dei gruppi abeliani TorR_n (A, B) per n = 0, 1, 2 TorR₀ (A, B) coincide con A⊗_RB, prodotto tensoriale di A e B su R.

Vi sono delle proprietà gradevoli (alcune delle quali saranno chiamate ‛funtoriali' nel capitolo successivo) che rendono facile l'impiego di Ext e Tor. L'argomento più usato è quello della lunga successione esatta che proviene da una successione esatta corta. (Una successione di omomorfismi è esatta se ad ogni passo il nucleo di una applicazione è l'immagine di quella precedente). Per esempio, l'esattezza di

0 →A → B→ C→ 0

induce sia l'esistenza di opportuni omomorfismi ‛di connessione', sia l'esattezza di

Extⁿ(C, D) → Extⁿ(B, D) → Extⁿ(A, D) →

→ Extⁿ⁺¹(C, D) → Extⁿ⁺¹(B, D) → Extⁿ⁺¹(A, D) ...

La coomologia di gruppi è un caso speciale di Ext; vediamo come. Siano dati un gruppo G ed un G-modulo A. Passiamo da G all'anello di gruppo ZG; A risulta allora uno ZO-modulo, ma prima di poter formare Ext abbiamo bisogno di un altro ZG-modulo, che ci sarà fornito dalla cosiddetta applicazione di aumento. Il nucleo I dell'omomorfismo naturale da ZG a G, che si ottiene mandando ogni elemento del gruppo in 1, si dice ideale di aumento; il nostro secondo modulo è ZG/I o, in altre parole, Z agisce su ZG facendo agire il gruppo in modo banale, e il gruppo di coomologia Hⁿ(G, A) è Extn_ZG(Z, A). La coomologia delle algebre associative e quella delle algebre di Lie si possono descrivere in modo analogo.

Ad Ext si accompagna una nozione di dimensione omologica; diciamo che la dimensione proiettiva di un modulo A è n, se Extⁿ⁺¹(A, B) = O per tutti i moduli B e se n è il più piccolo degli interi per cui ciò accade. Se non esiste un tale n, la dimensione è ∞. L'estremo inferiore delle dimensioni di tutti i moduli è la dimensione globale dell'anello. (Più precisamente, si tratta della dimensione globale destra per i moduli a destra, oppure della dimensione globale sinistra per i moduli a sinistra. Se la dimensione non è 0, non vi è nessuna connessione tra le dimensioni globali a sinistra e quelle a destra di un anello qualunque).

Un modulo con dimensione omologica zero si dice proiettivo; i moduli proiettivi sono identici agli addendi diretti dei moduli liberi.

La nozione di dimensione globale si adatta bene ai concetti antecedenti nella teoria degli anelli; un anello ha dimensione globale O se, e solo se, è artiniano semisemplice, ed un dominio commutativo ha dimensione globale ≤ 1 se e solo se è di Dedekind. (I domini di Dedekind formano una classe di anelli leggermente più ampia dei domini a ideali principali; essi sono gli anelli che compaiono nella teoria dei numeri algebrici. Possono caratterizzarsi richiedendo che ogni loro ideale sia un prodotto di ideali primi. In algebra omologica, si preferisce richiedere che ogni loro ideale sia proiettivo, il che è un altro modo per dire che la dimensione globale è al più 1).

Un punto notevole nell'applicazione dell'algebra omologica alla teoria degli anelli è costituito dal teorema di Auslander, Buchsbaum e Serre (1955) secondo cui un anello locale ha dimensione globale finita se, e solo se, è regolare. Quattro anni più tardi, Auslander e Buchsbaum estesero talmente i metodi omologici da poter rispondere ad una questione lasciata aperta per oltre venti anni da Krull; essi dimostrarono, come si è accennato nel capitolo precedente, che ogni anello locale regolare è un dominio a fattorizzazione unica.

Imponendo che Ext si annulli sulla seconda variabile anziché sulla prima, si ha una nozione duale di dimensione omologica. Inoltre, diciamo che B ha dimensione iniettiva n se Extⁿ⁺¹(A, B) = 0 per ogni A e se n è minimale rispetto a tale proprietà. Ciò conduce, a sua volta, alla dimensione iniettiva globale che, tuttavia, non è nulla di nuovo in quanto coincide con la dimensione proiettiva globale. Un modulo con dimensione iniettiva nulla si dice iniettivo. I moduli iniettivi sono esattamente gli addendi diretti di ogni modulo che li contiene; si tratta di un concetto introdotto da Baer nel 1940.

All'annullarsi di Tor è legato un altro tipo di dimensione per un modulo, detta dimensione debole; un modulo con dimensione debole zero è piatto. Anche questa nozione è legata a concetti più vecchi; per esempio, un anello ha dimensione debole O se, e solo se, è regolare di von Neumann (cioè, per ogni a esiste un x per cui axa = a).

Le tre classi di moduli testé menzionate - proiettivi, iniettivi, piatti - sono ormai entrate a far parte del patrimonio culturale non solo degli algebristi, ma anche dei matematici specializzati in altri settori. Infatti, facciamo notare, a titolo di esempio, un legame tra moduli proiettivi e topologia (Swan, 1962): se X è uno spazio di Hausdorff compatto, vi è una corrispondenza naturale biunivoca fra i fibrati vettoriali su X e gli R-moduli proiettivi con un numero finito di generatori, dove R è l'anello delle funzioni reali continue su X.

I moduli proiettivi hanno spesso un tipo di completezza forte che unifica un numero sorprendentemente alto di fenomeni sorti precedentemente caso per caso. Ne citiamo due, senza entrare nei dettagli: completezza degli anelli di Boole e massimalità degli anelli di valutazione.

Il teorema di Baer (1940), secondo cui ogni modulo può essere immerso in un modulo iniettivo, è notevolmente più difficile del suo duale proiettivo, in base al quale ogni modulo è immagine omomorfa di un modulo proiettivo (il che è banale, in quanto il modulo proiettivo può essere scelto libero fin dall'inizio). Ma v'è di più; Fckmann e Schopf (1953) scoprirono una certa inclusione ‛minimale' di un modulo dentro un modulo iniettivo e ne dimostrarono l'unicità a meno di isomorfismi. Qui, la nozione chiave è quella di ampliamento essenziale B di un modulo A, cioè tale che A ha intersezione diversa da zero con ogni sottomodulo non zero di B. La conclusione è che ogni modulo C è contenuto in un modulo iniettivo D, che ne è un ampliamento essenziale, e due moduli D siffatti sono isomorfi mediante una applicazione la cui restrizione a C è l'identità. Si dice anche che D è un inviluppo iniettivo di C.

Per quanto riguarda i moduli piatti, l'esperienza fatta fino ad ora giustifica la seguente osservazione: dati un anello R ed un anello S che sia un ‛grande' ampliamento di R, il buon comportamento di S è, in numerosi casi importanti, legato strettamente al fatto che S sia un R-modulo piatto.

Concludendo, ricordiamo un teorema di Stallings (1968), che in seguito Swan perfezionò (1969) eliminando l'ipotesi che il gruppo avesse un numero finito di generatori: se G è un gruppo e H²(G, A) = O per tutti i G-moduli A (ciò si può anche esprimere dicendo che la dimensione coomologica di G è 1), allora G è libero. La dimostrazione del teorema precedente è importante poiché essa fa intervenire in larga misura tecniche di topologia algebrica in un problema puramente algebrico.

18. Categorie

Nello studio di strutture matematiche, quali per esempio gli insiemi, i gruppi e gli spazi topologici, certe convenienti applicazioni fra gli oggetti di tali strutture sono importanti quanto gli oggetti stessi. Nei tre esempi suddetti esse sono, rispettivamente, tutte le possibili applicazioni, gli omomorfismi, le applicazioni continue. Per designarle in tutti i casi possibili, la scuola francese suggerì il termine generico ‛morfismo' (ottenuto sopprimendo in ‛omomorfismo' il prefisso ‛omo') e questo suggerimento è stato largamente adottato.

Le proprietà essenziali in questa teoria furono postulate da Eilenberg e MacLane (1945) nei loro assiomi sulle ‛categorie'. In una categoria si ha un insieme di oggetti (A, B, ...) ed un insieme di morfismi ciascuno dei quali ha un oggetto iniziale A, uno finale B, ed è rappresentato mediante una freccia A B tra l'uno e l'altro. Notiamo che qui un morfismo non è una concreta applicazione tra insiemi, ma è come il fantasma di una applicazione invisibile. Gli assiomi sono i seguenti: 1) esiste una composizione di morfismi da A a B con morfistni da B a C, che fornisce morfismi da A a C; 2) tale composizione è associativa, nella misura in cui ciò ha senso; 3) per ogni oggetto A, vi è un morfismo identità da A a se stesso con le ovvie proprietà.

Il concetto di categoria comprende un campo sorprendentemente vasto di strutture matematiche. Si presentano due casi estremi: esiste un solo oggetto in una categoria C, e C è allora un semigruppo con unità, o monoide; non vi sono morfismi tra oggetti differenti e vi è solo il morfismo identità tra un oggetto e se stesso, nel qual caso la categoria è un insieme astratto.

Le idee che normalmente associamo ad elementi e funzioni, possono di solito essere adattate alle categorie, cambiando opportunamente il punto di vista; per esempio, la regola di semplificazione (a destra o a sinistra) può servire a sostituire la ‛biunivocità' e la ‛surgettività'; nella teoria delle categorie si usano i termini monomorfismo ed epimorfismo, rispettivamente. (Vi è qui una sottigliezza: se una data categoria consiste di applicazioni concrete, può darsi che i monomorfismi non siano realmente biunivoci o che gli epimorfismi non siano surgettivi).

Si possono definire i prodotti: un oggetto C è un prodotto di A e B se esistono due ‛proiezioni' π₁ e π₂ di C in A e in B tali che ogni morfismo da C ad un quarto oggetto D sia univocamente determinato dalle composizioni di π₁ e π₂ con opportuni morfismi da A e B a D, come indicato nel diagramma:

Cambiando il verso a tutte le frecce, si ottiene la nozione duale di coprodotto. Generalmente, le categorie si prestano egregiamente a trattare la dualità. Per ogni categoria, si ottiene la categoria duale invertendone ogni morfismo.

È utile, per la chiarezza, descrivere il prodotto e il coprodotto in alcune categorie familiari e cercare di definirlo in categorie nuove. Nella categoria degli insiemi, il prodotto è quello cartesiano e il coprodotto è l'unione disgiunta; nella categoria dei gruppi il prodotto è il prodotto diretto (prodotto cartesiano con l'operazione di composizione definita componente per componente) e il coprodotto è il prodotto libero (il gruppo più ‛generale' contenente una copia per ciascuno dei gruppi dati); nella categoria dei gruppi abeliani, sia il prodotto che il coprodotto sono la somma diretta.

La categoria dei gruppi abeliani ha altri tratti caratteristici che meritano attenzione: l'insieme dei morfismi tra due oggetti ha una struttura di gruppo abeliano e la composizione di morfismi è additiva in relazione a queste strutture di gruppo. Se postuliamo tali proprietà e ne assumiamo certe altre - come l'esistenza di nuclei (e dualmente di conuclei) con proprietà opportune - giungiamo al concetto di categoria abeliana. In una categoria abeliana, le successioni esatte hanno senso, e si può sviluppare in esse buona parte dell'algebra omologica. (Quando si presentano oggetti proiettivi ed iniettivi, si può aggirare l'ostacolo mediante opportuni accorgimenti).

Una proposizione campione è il ‛lemma dei cinque', secondo cui, nel diagramma seguente, il morfismo f₃ è un isomorfismo (cioè monomorfismo ed a un tempo epimorfismo) quando f₁ , f₂ , f₄, f₅ a sono isomorfismi e le righe sono esatte:

Se parliamo di gruppi abeliani e di omomorfismi effettivi, questa proposizione può dimostrarsi senza difficoltà, semplicemente ‛inseguendo' con pazienza gli elementi, a mano a mano che questi si muovono nel diagramma. In una categoria abeliana, la prima impressione è che la scarsità di elementi da inseguire sia un ostacolo serio alla dimostrazione; tuttavia il lemma dei cinque e numerosi altri risultati consimili sono stati stabiliti in categorie abeliane arbitrarie. Ma si è fatto anche di più: un teorema generale (stabilito più o meno indipendentemente da Freyd, Heron, Lubkin e Mitchell intorno al 1964) asserisce che ogni categoria abeliana può essere presentata come categoria di moduli su un anello conveniente.

Non dobbiamo perdere di vista il fatto che le categorie sono esse stesse un tipo di sistema algebrico. Esse differiscono da quelli usualmente studiati soprattutto perché l'operazione è definita solo parzialmente. Cionondimeno, il concetto di ‛omomorfismo' tra due categorie ha una definizione molto naturale; Eilenberg e MacLane gli diedero il nome molto suggestivo di funtore. (Usarono la parola ‛categoria' in onore di Aristotele e Kant, e la parola ‛funtore' in onore di Carnap). Gli Ext e Tor, discussi nel capitolo precedente, sono esempi illuminanti; come abbiamo già detto, il fatto di essere funtori è il motivo essenziale della loro utilità.

Oggi la teoria delle categorie sta sviluppandosi rapidamente e ne stanno proliferando applicazioni in tutta la matematica. Poiché un panorama adeguato va oltre i limiti del nostro lavoro, ci limiteremo ad accennare ad un argomento finale: quello dei funtori aggiunti, introdotti nel 1958 da Kan. Prima descriviamo un po' più precisamente i funtori. Siano C e D due categorie; un funtore F da C a D assegna ad ogni oggetto A in C un oggetto FA in D e ad ogni morfismo f:A→B un morfismo Ff:FA→FB. Si richiede inoltre che F conservi prodotti e identità. Più esattamente F è un funtore covariante. Un funtore controvariante da C a D è descrivibile come un funtore covariante da C all'opposto D* di D, dove D* è ottenuto da D cambiando verso a tutte le frecce. Per esempio, Ext(A, B) è covariante in B e controvariante in A, mentre Tor è covariante in ambedue le variabili. Supponiamo di avere inoltre un funtore G da D a C. Allora, dati A in C e B in D possiamo confrontare i morfismi da B a FA con quelli da GB ad A. G è un funtore aggiunto di F se queste due classi di morfismi sono legate appropriatamente. Piuttosto che entrare nei dettagli tecnici su quella che deve essere la ^trelazione opportuna' preferiamo considerare un esempio.

Sia G la categoria dei gruppi ed S quella degli insiemi. Si può definire un funtore F da G ad S, applicando ogni gruppo nell'insieme soggiacente (cioè, ‛dimenticando' la struttura di gruppo, il che suggerisce per F il nome di ‛funtore distratto'). Il funtore F ha un funtore aggiunto: quello che assegna ad ogni insieme il gruppo libero generato dagli elementi dell'insieme. L'essenza di quello che stiamo dicendo è che, se X è il gruppo libero su un insieme di generatori Y, e Z è un gruppo, allora gli omomorfismi di X in Z sono identificabili con le applicazioni dell'insieme Y in Z.

Non sempre esiste un funtore aggiunto ad un dato funtore; utili teoremi danno delle condizioni sufficienti per l'esistenza. Un funtore aggiunto è, in un certo senso, una soluzione al problema di costruire un oggetto ‛universale' e le condizioni in questione sono del tipo adatto a tali costruzioni.

Dal 1962 in poi, sono apparsi molti trattati sulle categorie. L'ultima trattazione, in ordine di tempo, è quella di MacLane (v., 1971).

19. Questioni varie

In questo capitolo finale, accenniamo brevemente ad argomenti importanti, che abbiamo dovuto sacrificare per ragioni di spazio.

a) Teoria dei reticoli

Il concetto di ordine è fondamentale in buona parte della matematica. Basta, per convincersene, pensare ai numeri reali per i quali la relazione di ordine è importante quanto le operazioni di addizione e moltiplicazione. Pertanto, la teoria degli insiemi ordinati' è un capitolo fondamentale dell'algebra.

La nozione di base è quella di insieme parzialmente ordinato, cioè di una relazione ≤ soddisfacente le condizioni di riflessività (a ≤ a), anti-simmetria (a ≤ b e b ≤ a implicano a = b) e transitività (a ≤ b e b ≤ c implicano a ≤ c). Se due elementi qualsiasi sono confrontabili, l'insieme parzialmente ordinato è una ‛catena'; all'estremo opposto, se due elementi diversi qualsiasi non sono confrontabili, allora l'insieme parzialmente ordinato è una ‛anticatena'.

Queste semplici definizioni danno luogo a problemi di sorprendente delicatezza. Consideriamo il problema di Souslin, che può essere posto come segue. Sia P un insieme parzialmente ordinato, in cui ogni catena ed ogni anticatena sono numerabili; P è numerabile? Solovay e Tenenbaum (1971) dimostrarono che, sulla base degli assiomi della matematica odierna, questo problema è assolutamente indecidibile.

Le consuete definizioni di estremo superiore ed estremo inferiore sono applicabili in un insieme parzialmente ordinato. Se due elementi qualsiasi, in un insieme parzialmente ordinato P, hanno un estremo inferiore ed un estremo superiore, P si chiama un ‛reticolo'; in genere, per l'estremo inferiore si usa la notazione x ⋀ y e per l'estremo superiore la notazione x ⋀ y.

Un reticolo può essere considerato come un sistema con due operazioni binarie che soddisfano certe identità; come tali, i reticoli si adattano allo schema generale dell'algebra moderna. Di particolare interesse è la possibilità di imporre identità addizionali; vi sono due identità siffatte, dette legge modulare e legge distributiva. Un reticolo, con un elemento massimo 1 ed un elemento minimo O, è complementato se, per ogni x, esiste un y per cui x ⋀ y = 1 x ⋀ y = 0. Le algebre di Boole sono reticoli distributivi complementati.

Vi è una notevole connessione tra la teoria dei reticoli e i fondamenti della geometria; con qualche piccola ipotesi aggiuntiva, un reticolo modulare complementato è esattamente la stessa cosa che il reticolo di tutti i sottospazi di un opportuno spazio proiettivo.

Il riferimento bibliografico tipico per la teoria dei reticoli è il libro di Birkhoff (v., 1967³).

b) Algebre di Hopf

La dualità appare così spesso in ogni parte dell'algebra che, prima o poi, tutto sarà probabilmente dualizzato. Consideriamo un'algebra A su un corpo k. A prima vista, la prospettiva di dualizzare sembra remota, ma se ricostruiamo la moltiplicazione come una applicazione lineare del prodotto tensoriale A ⊗_k A in A, il concetto duale diventa visibile: una coalgebra deve essere data da una applicazione lineare A→A ⊗_k A. Un'algebra di Hopf è simultaneamente un'algebra e una coalgebra appropriatamente legate tra loro.

Per quanto la nostra esposizione non segua lo sviluppo storico, ecco come è nata l'idea. Dai gruppi di coomologia di una varietà topologica, si può costruire un anello usando come moltiplicazione il cup product. Hopf (1941) osservò che se la varietà è un gruppo topologico (bastano di fatto condizioni più deboli) esiste una moltiplicazione sull'omologia e quindi una comoltiplicazione sulla coomologia; in breve, si ha un'algebra di Hopf. Partendo da qui, Hopf riuscì a determinare, con grande precisione, la struttura dell'anello di coomologia. Il teorema, presentato più tardi da Milnor e Moore (1965), in forma rifinita, ha bisogno delle seguenti ipotesi: un'algebra di Hopf A su un corpo perfetto k (cioè un corpo privo di ampliamenti non separabili); una graduazione su A in modo che la parte di grado O sia proprio k (si dice allora che A è connessa); opportune ipotesi di commutatività. La conclusione è che A si ottiene da algebre di polinomi ed algebre esterne.

Le algebre di Hopf compaiono in molti altri contesti. Eccone alcuni: 1) ogni algebra di gruppo è un'algebra di Hopf; 2) l'algebra inviluppo universale di un'algebra di Lie è un'algebra di Hopf; 3) i Tor che nascono da un anello locale formano un'algebra di Hopf; 4) una conveniente algebra di Hopf può sostenere il ruolo di un gruppo di Galois per ampliamenti non separabili di un corpo; 5) i gruppi algebrici ed i gruppi formali sono intimamente legati alle algebre di Hopf.

Una esposizione recente sulle algebre di Hopf è la monografia di Sweedler (v., 1969).

c) K-teoria algebrica

I topologi hanno utilizzato, per un certo tempo, un metodo importante per associare ad uno spazio topologico X e ad un intero n un certo gruppo abeliano Kⁿ(X). Tale teoria, detta K-teoria topologica, ha molte delle proprietà di una teoria della coomologia.

Nel 1963, Bass (aiutato inizialmente da Schanuel) si accorse che alcuni oggetti simili - almeno per quanto riguarda K⁰ e K¹ - si potevano associare ad un anello arbitrario. Nacque così la K-teoria algebrica.

Per costruire K⁰(R), si prendono gli R-moduli proiettivi con un numero finito di generatori con l'operazione di somma diretta e, dopo una conveniente identificazione, se ne fa un gruppo abeliano. (Un modo agevole di vedere la questione è un artificio di Grothendieck che riesce ad associare un gruppo abeliano a quasi ogni cosa). Ovviamente, se i suddetti P-moduli proiettivi sono anche liberi, K⁰(R) non ha alcun interesse. Per vederne la connessione con la topologia, osserviamo che il K⁰ topologico è ottenuto da fibrati vettoriali e che (come si è notato nel cap. 17) i fibrati vettoriali sono identificabili con certi moduli proiettivi.

K¹(R) è, a prima vista, un oggetto ben differente; per averne un'idea consideriamo il caso commutativo. Sia O il gruppo lineare n × n (costituito da tutte le matrici invertibili n × n) e sia U il suo sottogruppo unimodulare (matrici di determinante 1). Evidentemente U contiene il sottogruppo commutatore [G, G]. (Il sottogruppo commutatore di un gruppo consiste di tutti i prodotti di commutatori x^-1y^-1xy, al variare di x e y nel gruppo; esso è il più piccolo sottogruppo normale, tale che il gruppo quoziente, rispetto a quel sottogruppo normale, sia abeliano). U e [O, O] sono uguali per n ≥ 3? (La questione si pone solo per n ≥ 3, perché per n = 2 vi sono eccezioni banali). La risposta è negativa e K¹ misura lo scarto. Più precisamente, bisogna ‛stabilizzare' il problema facendo tendere n all'infinito, con qualche aggiustamento nel caso non commutativo.

Il passaggio da R a R[x] non è particolarmente interessante, ma vi è una relazione sorprendente tra K⁰(R) e K¹(R[x, x^-1]), che ricorda i teoremi di periodicità di Bott in topologia.

Sia I un ideale bilatero in R. Si possono definire i gruppi relativi K⁰(R, I), K¹(R, I) e, dalla successione esatta

0 → I → R → R/I → 0

si ottiene la successione esatta

O →K⁰ (R, I) → K⁰(R) → K⁰(R/I) →

→ K¹(R, I) → K¹(R) → K¹(R/I).

Si trova che il gruppo K¹(R, I) dipende solo dall'ideale I e non dall'anello R che lo contiene. Pertanto esso può scriversi K¹(I).. Così gli anelli senza unità, eliminati per sempre da Bourbaki, hanno fatto la loro ricomparsa nella K-teoria algebrica.

Molte vie sono state tentate per definire i Kⁿ successivi (cosa desiderabile, se non altro per potere estendere all'infinito la successione precedente). Fino a questo momento, i loro legami non sono stati completamente chiariti e resta ancora da esplorare la loro utilità potenziale. Comunque il K² proposto da Milnor ha già mostrato utili legami con i gruppi lineari e con la teoria dei numeri. (Recentemente, un lavoro conclusivo di Quillen ha posto su solide basi una teoria di Kⁿ (R) per ogni n).

Il trattato più vasto sulla K-teoria algebrica è il libro di Bass (1968).

d) Semigruppi

Nel corso di questo lavoro, abbiamo più volte nominato i semigruppi, ed ogni volta questi sono apparsi come qualche cosa posta in margine ad un altro argomento di primario interesse. Esiste, invece, un'importante teoria dei semigruppi, che costituisce una disciplina autonoma.

Tuttavia i semigruppi sono molto più numerosi dei gruppi. Nel 1955, con l'aiuto di un calcolatore elettronico, Forsythe trovò che vi sono 126 semigruppi di ordine 4 e tale risultato fu confermato da Tamura, senza l'impiego del calcolatore, nello stesso periodo di tempo. (Qui non si fa distinzione tra un semigruppo e quello opposto ottenuto invertendo la moltiplicazione). Vi sono tuttavia solo due gruppi di ordine 4: il gruppo ciclico e il prodotto diretto di due gruppi ciclici di ordine 2.

Una parte notevole della teoria dei semigruppi rassomiglia alla teoria degli anelli piuttosto che a quella dei gruppi. Un buon esempio è un teorema di Rees (1940) che ha una forte analogia con il teorema di struttura di Wedderburn per anelli semplici. Consideriamo un semigruppo 5 con lo O. Un ideale I in S è un sottoinsieme che assorbe la moltiplicazione da sinistra o da destra per gli elementi di S. S si dice semplice se non ha ideali eccetto O e S stesso. Un primo esempio di semigruppo semplice è dato da un gruppo a cui è stato aggiunto uno zero. Sia esso T. Da T si possono ottenere altri esempi, prendendo le matrici n × n su T che hanno al più un elemento diverso da 0. Estendiamo ancora questi esempi, autorizzando la moltiplicazione per una data matrice. Il teorema di Rees afferma che si ottengono così tutti i semigruppi finiti e che, anzi, si può indebolire la condizione di finitezza.

Il riferimento bibliografico tipico per i semigruppi 6 il trattato in due volumi di Clifford e Preston (v., 1961 e 1967).

e) Anelli noetheriani non commutativi

Si sono fatti parecchi tentativi di estendere al caso non commutativo la teoria, così ben sviluppata, degli anelli noetheriani commutativi. Visti in retrospettiva, questi tentativi hanno preso per lo più una direzione sbagliata. Per quanto il mistero continui ad avvolgere molti aspetti di questo argomento, un passo avanti venne fatto da Goldie (1958) con la dimostrazione del teorema seguente. Sia R un anello noetheriano senza ideali nilpotenti; allora R ha un anello quoziente Q, in un certo senso naturale, introdotto da Ore, che è anche semisemplice artiniano. Un teorema di Posner (1960) aggiunge un complemento significativo: se R soddisfa una identità polinomia, anche Q la soddisfa e pertanto, in tal caso, gli anelli con divisione che appaiono in Q sono di dimensione finita sui loro centri. La scoperta, dovuta a Formanek (v. cap. 10), dei polinomi centrali ha fornito informazioni ulteriori. Successivamente, l'ipotesi di noetherianità è stata indebolita e sono state trovate condizioni necessarie e sufficienti per l'esistenza di una inclusione del tipo di Goldie.

f) Algebre su anelli commutativi

Una tendenza persistente traspare dai lavori sulla teoria degli anelli: i teoremi dimostrati per le algebre su un corpo vengono, presto o tardi, generalizzati ad algebre su un anello commutativo. Dal 1960 in poi, si sono fatti grandi passi in questa direzione relativamente ai seguenti argomenti, legati tra loro: teoria di Galois, algebre semplici centrali, gruppo di Brauer.

Due articoli di Auslander e Goldman (1960) aprirono la strada. Prima di tutto generalizzarono la nozione di separabilità in un modo che illustra una volta di più quanto possa portare lontano il concetto di modulo proiettivo. Sia k un anello commutativo, sia R* un'algebra su k e sia R* l'algebra opposta; R 6, in modo naturale, un (R⊗_k R*)- modulo. Auslander e Goldman posero, per la separabilità di R su k, la condizione che questo modulo fosse proiettivo. Sebbene la definizione non faccia alcun cenno alla necessità che R sia ‛piccolo', di fatto (Villamayor e Zelinsky, 1966) se R è anche proiettivo come k-modulo, allora esso è un k-modulo con un numero finito di generatori.

Con questa nozione di separabilità, la teoria di Galois funziona per gli anelli commutativi, una volta che ci si limiti al caso in cui gli anelli intermedi siano separabili sull'anello di base. Se R 6 separabile su k e k 6 il centro di R, R si dice un'algebra centrale separabile o algebra di Azumaya. Se k 6 un corpo, il concetto si riduce a quello di algebra centrale semplice.

Un altro criterio consiste nel richiedere che A/MA sia centrale semplice sul corpo k/M per ogni ideale massimale M in k.

M. Artin (1969) ha dimostrato un importante teorema, che noi enunciamo nella forma migliorata datagli da Procesi (1972): R 6 centrale separabile se, e solo se, soddisfa tutte le identità delle matrici n × n e se nessuna immagine omomorfa di R soddisfa tutte le identità delle matrici (n − 1) × (n − 1).

Dalle algebre centrali separabili su k, si può ancora, mediante il prodotto tensoriale, formare un gruppo di Brauer. Questa possibilità di associare un gruppo di Brauer commutativo ad un qualsiasi anello commutativo ha, tra l'altro, aumentato la nostra comprensione del gruppo di Brauer di un corpo.

bibliografia

Albert, A. A., Structure of algebra, New York 1939 (rist. riveduta, 1961).

Bass, H., Algebraic K-theory, New York-Amsterdam 1968.

Birkhoff, G., Lattice theory, New York 1940, 1967³.

Bourbaki, N., Éléments de mathématique, Paris 1939 ss.

Burnside, W., Theory of groups of finite order, Cambridge 1911² (rist. New York 1955).

Cartan, H., Eilenberg, S., Homological algebra, Princeton 1956.

Chevalley, C., Fundamental concepts of algebra, New York 1956 (tr. it.: Concetti fondamentali di algebra, Milano 1964).

Clifford, A. H., Preston, G. B., The algebraic theory of semigroups, 2 voll., New York 1961 e 1967.

Fuchs, L., Infinite Abelian groups, 2 voll., New York 1970 e 1973.

Gauss, K. F., Disquisitiones arithmeticae, Lipsiae 1801.

Grothendieck, A., Dieudonné, J. A., Éléments de géometrie algébrique, Paris 1960 ss.; nuova ed.: vol. I, New York 1971.

Jacobson, N., Structure of rings, Providence 1956 (rist. riveduta, 1964).

Jacobson, N., Lie algebras, London 1962.

Jacobson, N., Structure and representations of Jordan algebras, Providence 1968.

Lang, S., Algebra, Reading, Mass., 1965 (rist. riveduta, 1971).

MacLane, S., Categories for the working mathematician, New York 1971.

MacLane, S., Birkhoff, G., Algebra, New York-London 1967.

Nagata, M., Local rings, New York 1962.

Neumann, J. von, Morgenstern, O., Theory of games and economic behavior, Princeton 1943, 1953³.

Passmann, D. S., Infinite group rings, New York 1971.

Sweedler, M., Hopf algebras, New York 1969.

Waerden, B. L. van der, Moderne Algebra, 2 voll., Berlin 1930 e 1931.

Zariski, O., Samuel, P., Commutative algebra, 2 voll., Princeton 1958 e 1962.