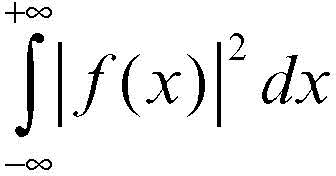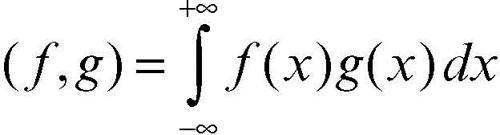analisi funzionale
analisi funzionale
analisi funzionale settore disciplinare che ha come oggetto di studio le funzioni o famiglie di funzioni, viste come elementi di opportuni spazi astratti, detti appunto spazi funzionali, e le operazioni lineari e non lineari definite su tali spazi e che dividono tale disciplina nei due settori principali. È possibile dotare gli spazi funzionali di strutture algebriche e topologiche (quali la struttura di spazio vettoriale, spazio metrico, spazio normato) ed è possibile estendere a essi i concetti di limite, derivata e integrale. Per esempio, la famiglia delle funzioni continue su un intervallo limitato [a, b] a valori in R, che si denota in generale con C([a, b]), è uno spazio vettoriale rispetto alle operazioni di somma e composizione di funzioni. L’elemento neutro rispetto alla somma è la funzione costante ƒ(x) = 0 e rispetto al prodotto è la funzione identica ƒ(x) = x entrambe definite su [a, b]. Inoltre è uno spazio di Banach rispetto alla norma così definita
L’insieme L2(R) delle funzioni ƒ definite su R tali che
risulta uno spazio di Hilbert rispetto al prodotto scalare così definito:
Si chiamano operatori le funzioni definite su spazi funzionali a valori in spazi funzionali. Poiché uno spazio normato è anche uno spazio topologico, è possibile estendere il concetto di limite agli operatori definiti su spazi di Banach e di Hilbert.
Nell’ambito dell’analisi funzionale è possibile studiare in astratto importanti problemi ed enti matematici, tra cui quelli classici dell’analisi: le equazioni differenziali alle derivate parziali, il calcolo delle variazioni, la teoria dell’ottimizzazione, la teoria della probabilità, l’analisi numerica e i problemi di approssimazione.
La grande varietà di scelte celate nelle strutture astratte legate agli spazi funzionali ha permesso di trattare in modo unificato (per linguaggio e per teoremi) un gran numero di problemi apparentemente dissimili. Più modernamente, la teoria degli spazi vettoriali topologici definisce spazi ancor più generali, adatti a descrivere per esempio le distribuzioni, che forniscono una generalizzazione del concetto di funzione.
L’analisi funzionale, sviluppatasi soprattutto nel Novecento, costituisce una delle espressioni più significative della matematica contemporanea. Storicamente, sono considerati iniziatori dell’analisi funzionale (per lo meno nel suo aspetto moderno) V. Volterra e D. Hilbert, con i loro lavori sulle equazioni funzionali, equazioni nelle quali l’incognita è rappresentata da una funzione. Uno dei problemi che hanno dato origine all’analisi funzionale è l’equazione integrale di → Fredholm di seconda specie. I primi risultati sull’esistenza e l’unicità delle soluzioni di tale equazione furono ottenuti dallo stesso Fredholm che utilizzò, tra gli altri, gli studi di J. Hadamard sui determinanti; questi primi risultati furono completati e generalizzati da Hilbert ed E. Schmidt, che utilizzarono metodi così generali da poterli annoverare tra quelli dell’analisi funzionale. Verso il 1918 F. Riesz, generalizzando i risultati di Hilbert, fece rientrare la risoluzione dell’equazione di Fredholm nella teoria degli operatori lineari compatti su spazi vettoriali normati, completi, oggi chiamati spazi di Banach (lo sviluppo dell’analisi funzionale è stato sempre fortemente debitore della topologia). A partire dal 1920 l’analisi funzionale si sviluppò rapidamente per arrivare, nel 1935, alla definizione, dovuta a J. von Neumann, di spazi vettoriali localmente convessi. Lo studio delle equazioni integrali, differenziali ordinarie e alle derivate parziali, il calcolo delle variazioni, l’analisi armonica, il calcolo delle probabilità hanno poi contribuito allo sviluppo dell’analisi funzionale e, a loro volta, hanno beneficiato dei progressi di quest’ultima, mentre lo sviluppo precedente era stato sollecitato dalle teorie della fisica-matematica (elettromagnetismo, relatività, meccanica quantistica), dalla meccanica del continuo (elasticità, idrodinamica ecc.), dall’ottimizzazione di soluzioni problemi complessi. Molte classi di problemi posti all’analisi matematica dalle scienze fisiche, dall’economia, dalla biologia ecc., o anche problemi interni alla matematica stessa, che si traducono in equazioni differenziali, equazioni integrali, integro-differenziali, possono essere proficuamente interpretati negli spazi funzionali come «problemi geometrici» e le soluzioni sono date da punti di tali spazi. In tali spazi si costruiscono una teoria della misura, dell’integrazione; si studiano trasformazioni fra tali spazi (cioè corrispondenze che associano a un elemento di uno spazio astratto un elemento di un altro spazio astratto). Una opportuna formulazione dei problemi in questa visione astratta e generale consente di prescindere da certi aspetti contingenti del problema in esame per metterne in evidenza il carattere essenziale, che nella maggior parte dei casi viene interpretato in termini di trasformazioni fra certi spazi funzionali. Questo atteggiamento, tipico dell’analisi funzionale, si è rivelato fecondo di risultati sia per la chiara visione del problema generale che consente sia per le potenti tecniche che suggerisce.