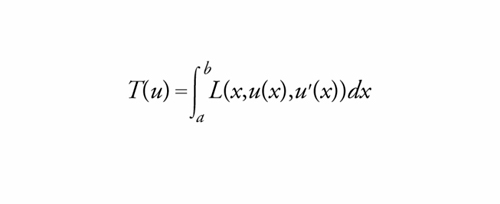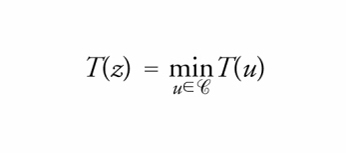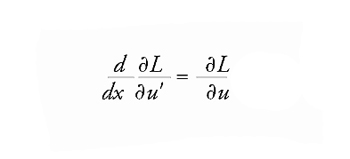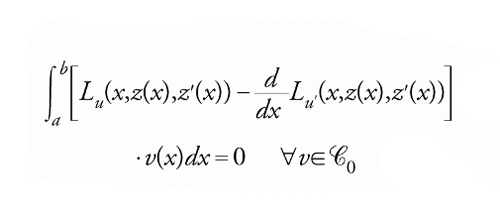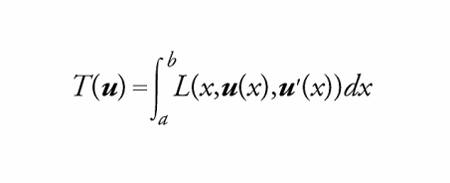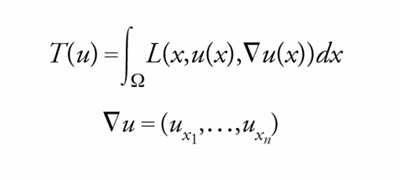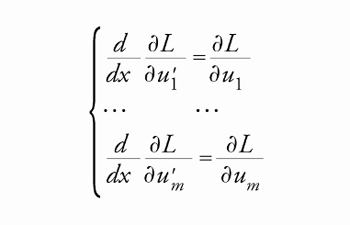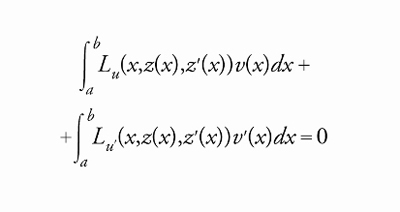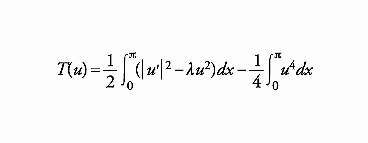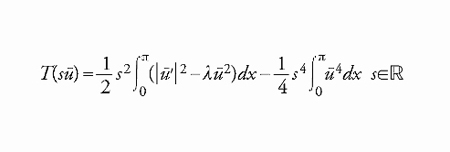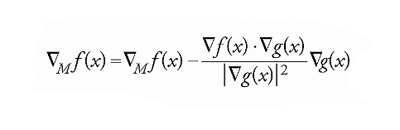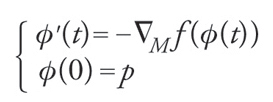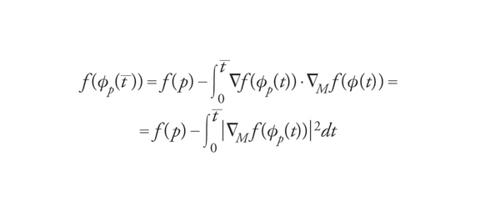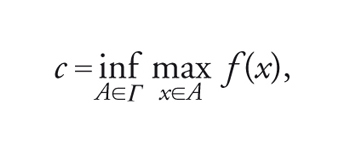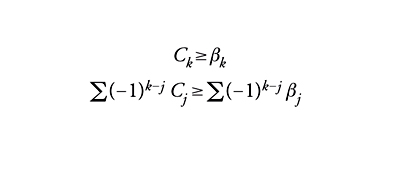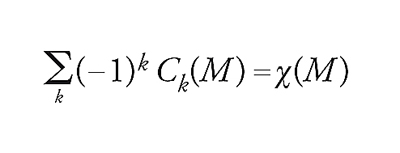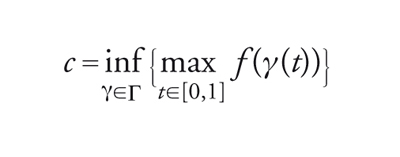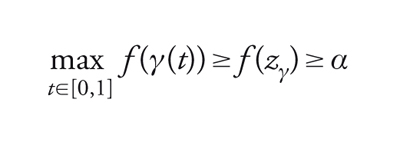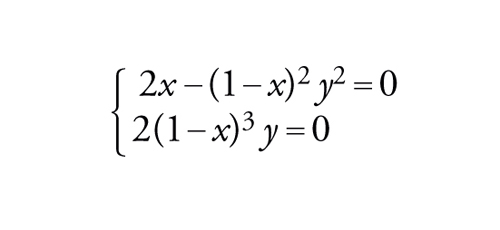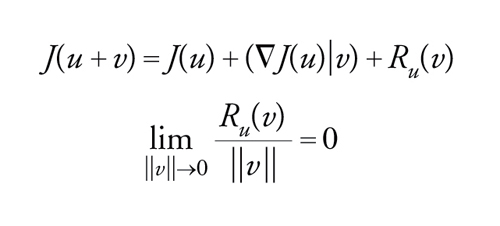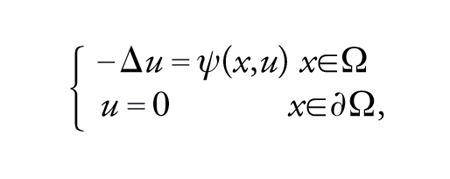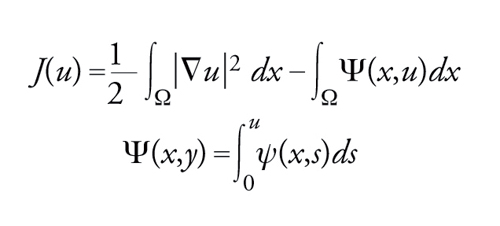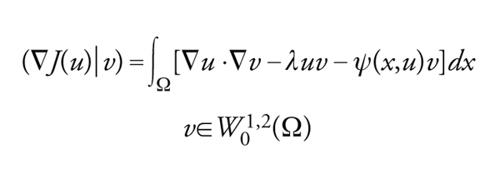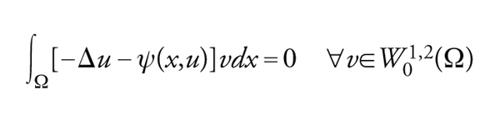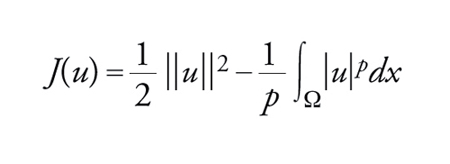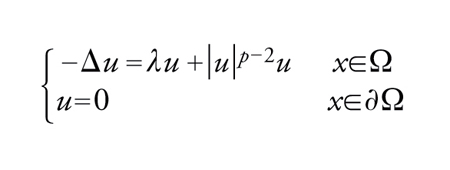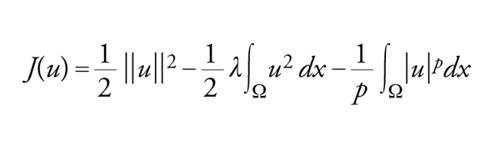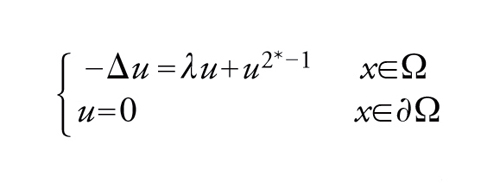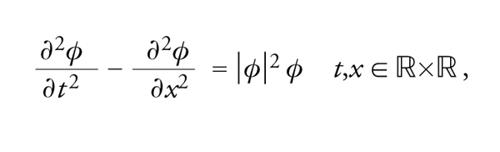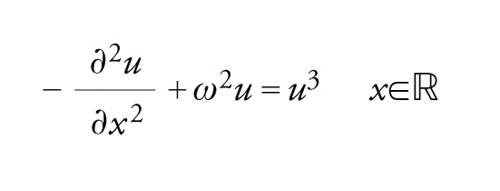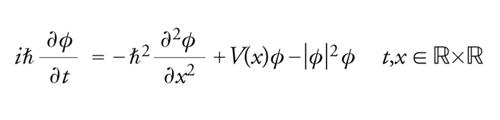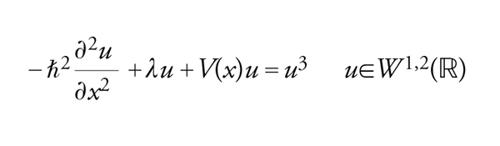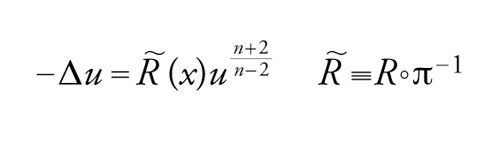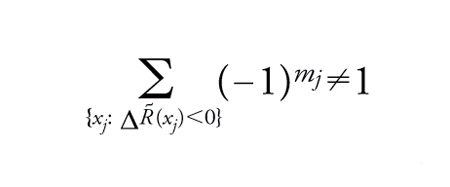Analisi non lineare: metodi variazionali
Analisi non lineare: metodi variazionali
I primi problemi di calcolo delle variazioni si presentano quasi spontaneamente, anche nello studio della geometria elementare e hanno infatti attratto l'interesse dei matematici fin dall'antichità. Per esempio, nel libro VI degli Elementi di Euclide si affronta il problema di trovare, tra tutti i rettangoli con perimetro assegnato, quello di area massima. Un semplice calcolo mostra che la risposta corretta è un quadrato. Questo è un caso particolare del problema isoperimetrico per i poligoni piani: tra i poligoni con un dato numero di lati e con perimetro assegnato, qual è quello di area massima? La risposta ‒ il poligono regolare con il corrispondente numero di lati ‒ era nota a matematici come Zenodoro e Pappo diversi secoli prima dell'inizio dell'era cristiana.
Altri problemi di calcolo delle variazioni, che è possibile studiare utilizzando tecniche sostanzialmente elementari sono quello della riflessione della luce, già risolto nell'antichità da Erone, e quello della sua rifrazione, studiato all'inizio del Seicento da Willebrordus Snellius, René Descartes e Pierre de Fermat.
Tuttavia, l'inizio del moderno calcolo delle variazioni si fa di solito risalire al problema della brachistocrona, posto dapprima da Galileo Galilei e in seguito, in maniera completa, dal matematico svizzero Johann Bernoulli. Si tratta del problema seguente: dati due punti in un piano verticale, si consideri una massa puntiforme che cade, con velocità iniziale nulla e soggetta solo alla forza di gravità, lungo una curva che congiunge i due punti. Tra tutte le traiettorie possibili, qual è quella lungo la quale la massa puntiforme impiega il minimo tempo per andare da un punto all'altro? La soluzione fu trovata nel 1697 dallo stesso Johann Bernoulli ‒ e indipendentemente da suo fratello Jakob, oltre che da Gottfried Leibniz e Isaac Newton: la traiettoria cercata è un arco di cicloide. In seguito furono posti e risolti diversi problemi simili, come quello della catenaria, della superficie di rivoluzione di area minima e il problema del solido di minima resistenza in un fluido. Tutti presentano un'importante novità: per la prima volta l'incognita che occorre determinare è una funzione.
La ricerca di risultati generali per problemi di minimo di questo tipo portò Leonhard Euler e Joseph-Louis Lagrange a formulare una condizione necessaria, sotto forma di un'equazione differenziale, per l'esistenza di minimi (o massimi). Si ottiene così una procedura canonica per affrontare e risolvere problemi di minimo del calcolo delle variazioni: si cerca una soluzione dell'equazione di Euler-Lagrange e poi si prova che essa fornisce effettivamente il minimo cercato. In seguito furono formulate, per esempio da Carl G.J. Jacobi, anche delle condizioni sufficienti per la risoluzione del problema di minimo.
Un punto di vista del tutto nuovo nell'affrontare questo tipo di problemi fu dato all'inizio del secolo scorso dall'introduzione dei metodi diretti da parte di David Hilbert e poi, in Italia, da Leonida Tonelli. L'idea è che invece di passare attraverso la risoluzione dell'equazione di Euler-Lagrange, si affronta direttamente il problema dell'esistenza del minimo. Applicando questi metodi Hilbert "richiamò in vita" ‒ come egli disse ‒ il principio di Dirichlet.
I metodi diretti hanno aperto nuove prospettive di ricerca anche per affrontare lo studio dei problemi non lineari di tipo variazionale. Infatti, non solo i minimi ma tutti i punti critici di un funzionale sono soluzioni dell'equazione di Euler-Lagrange e in molti casi può accadere che le soluzioni non banali di tale equazione siano invece dei punti di sella. La loro determinazione è l'obiettivo della teoria dei punti critici, che ha avuto un enorme sviluppo negli ultimi cento anni e attualmente rappresenta uno dei filoni di ricerca più attivi nell'analisi matematica.
Un differente metodo, elegante e preciso, per determinare i punti critici di un funzionale su una varietà compatta dello spazio euclideo n-dimensionale si fonda invece sull'uso di profonde proprietà topologiche: si tratta dalla teoria sviluppata negli anni Trenta da Marston Morse. Nel caso non compatto, una condizione che sostituisce la compattezza è stata introdotta in seguito da Richard S. Palais e Steven Smale. I risultati ottenuti per spazi euclidei sono stati opportunamente estesi a spazi funzionali di dimensione infinita, anche nel caso in cui non vale la condizione di Palais e Smale, grazie a lavori di Haïm Brézis, Louis Nirenberg e più recentemente di Pierre-Louis Lions.
Il calcolo delle variazioni moderno
In matematica accade spesso che vengano posti dei problemi specifici, che sono risolti in modo brillante con metodi particolari. Successivamente, però, si sente la necessità di inquadrarli in una cornice astratta. In questo modo, si ha una visione d'insieme che spesso è molto utile per trovare delle regole generali per risolvere i problemi posti. Naturalmente, non si potranno sempre ottenere risultati di grande precisione, per i quali occorrerà ritornare ai vari casi particolari.
Il discorso vale anche per i problemi del calcolo delle variazioni. La ricerca di tecniche generali per la determinazione, sulla classe C delle funzioni u:[a,b]→ℝ, regolari e tali che u(a)=α e u(b)=β, del minimo di Funzionali della forma
[1] formula
dove la funzione L(x,u(x),u′(x)) è detta lagrangiana, por-tò Leonhard Euler e Joseph-Louis Lagrange a formulare una condizione necessaria per l'esistenza di minimi (o massimi).
Supponiamo infatti che la lagrangiana L sia regolare. Se z(x)∈C è tale che
[2] formula,
allora z verifica l'equazione di Euler-Lagrange (EL)
[3] formula.
È utile dare un cenno alla dimostrazione di questo risultato. Consideriamo una variazione della funzione z, z+εv. Indicata con C0 la classe delle funzioni regolari e verificanti v(a)=v(b)=0, si ha che z+εv∈C se e solo se v∈C0. Per ogni v∈C0, la funzione
[4] formula
è derivabile e ha un minimo in ε=0. Quindi si ha τ′(0)=0 per ogni v∈C0, che equivale a
[5] formula.
Integrando per parti nel secondo integrale si trova
[6] formula.
Infine, usando il fatto che la relazione precedente è vera per ogni v∈C0, si deduce la [3].
È opportuno fare un'osservazione che ci sarà utile nel seguito. I ragionamenti fatti valgono non solo nel caso che z sia un minimo per T in C: è sufficiente che la funzione reale τ(ε) abbia derivata nulla in ε=0, per ogni v∈C0. Le funzioni z che godono di questa prorietà sono chiamate punti critici di T (in C) e verificano l'equazione differenziale [3].
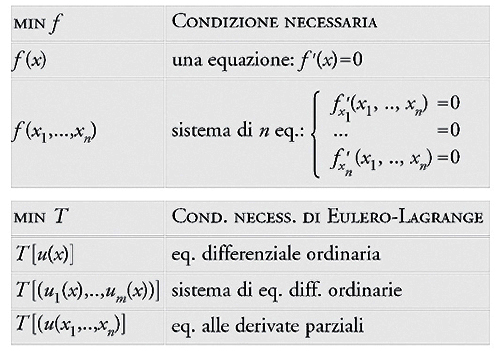
È anche chiara l'analogia con il caso elementare di una funzione regolare f : ℝ→ℝ. Come è ben noto, se x*∈ℝ è un massimo o un minimo di f, allora deve risultare f′(x*)=0. Se f è sostituita da un funzionale T, la relazione f′=0 si traduce in un'equazione differenziale, ovvero la [3]. Il risultato precedente fornisce una regola canonica per tentare di risolvere i problemi di minimo del calcolo delle variazioni. Si cerca di trovare una soluzione dell'equazione di Euler-Lagrange, provando poi che essa è effettivamente un minimo di T(u) nella classe C. Ma il suo interesse sta anche nel fatto che mette in luce uno stretto legame tra le equazioni differenziali del tipo [3] e i funzionali della forma [1].
Anticipando un discorso che faremo in modo più dettagliato e preciso nel seguito, ci limitiamo qui a osservare che, spostando l'attenzione primaria sull'equazione differenziale [3], possiamo usare i ragionamenti esposti prima per ottenere risultati di esistenza per essa. Infatti, se vogliamo provare che l'equazione differenziale [3] ha una soluzione nella classe C, basterà considerare il corrispondente funzionale T(u), e provare che esso ha un minimo (o un punto critico) in C. Vedremo più avanti come questo sia possibile e apra scenari di grande interesse.
Tornando alle condizioni necessarie di Euler-Lagrange, ricordiamo che esse valgono anche nel caso vettoriale e cioè per funzionali del tipo
[7] formula
dove u=(u1,…,um), oppure nel caso di integrali multipli, ovvero
[8] formula
dove Ω è un aperto limitato di ℝn e x∈Ω. In quest'ultimo caso la classe C sarà formata dalle funzioni u: Ω‒→ℝ, regolari e tali che u(x) coincide con una assegnatafunzione h(x) per x∈∂Ω (∂Ω indica la frontiera dell'aperto Ω).
Nel primo caso, la [3] diventa un sistema di m equazioni ordinarie
[9] formula
mentre nel secondo otteniamo un'equazione alle derivate parziali del secondo ordine:
[10] formula
dove uxi indica la funzione ∂u/∂xi
Qui di seguito vengono messe in evidenza le analogie con il caso elementare dei massimi e minimi di una funzione f(x).
Altre condizioni necessarie per l'esistenza di un minimo di T in C sono state formulate da vari matematici. Per esempio, Adrien-Marie Legendre stabilì che se z∈C è un minimo di T allora risulta
[11] Lu′u′(x,z(x),z′(x))≥0, ∀x∈[a,b].
Qui e nel seguito il pedice indica l'operazione di derivata parziale.
Successivamente, sono state date, per esempio da Karl Jacobi, anche delle condizioni sufficienti per la risoluzione del problema di minimo.
Per motivi di spazio, non possiamo qui soffermarci su queste ricerche e ci limitiamo a ricordare alcune difficoltà incontrate dai matematici del tempo. Un primo problema sta nel fatto che a volte T può avere minimo non in C ma in una classe C∼ più ampia, contenente funzioni meno regolari. Inoltre, l'equazione di Euler-Lagrange può non essere facilmente risolvibile perché si tratta, anche nei casi più semplici, di un'equazione del secondo ordine nonlineare o di un'equazione alle derivate parziali. Per esempio, se vogliamo trovare il minimo dell'integrale di Dirichlet
[12] formule
tra le funzioni u: Ω→ℝ regolari che assumono sul bordo ∂Ω un assegnato valore h(x,y), la corrispondente equazione di Euler-Lagrange è l'equazione di Laplace uxx+uyy=0 con le condizioni al contorno u(x,y)=h(x,y) per (x,y)∈∂Ω.
Questa equazione è ora considerata banale ma non era affatto tale per i matematici del tempo (parliamo degli anni a cavallo tra l'Ottocento e il Novecento), che avevano elaborato dei procedimenti risolutivi solo in casi molto particolari.
I metodi diretti nel calcolodelle variazioni
Nello studio di un certo problema si cerca spesso di affinare tecniche collaudate, usando mezzi sempre più sofisticati. Di norma si prosegue in questo modo fino a quando non insorgono difficoltà insormontabili: a questo punto è necessario un salto di qualità, per affrontare il problema in modo totalmente originale.
Per superare le difficoltà cui si è accenato nella sezione precedente era necessario un contributo nuovo furono David Hilbert e, in Italia, Leonida Tonelli a darlo. Invece di cercare di risolvere l'equazione di Euler-Lagrange essi affrontarono direttamente (da qui il nome di metodi diretti) il problema dell'esistenza del minimo di un funzionale T del tipo [1].
In breve, il procedimento seguito si basa sui seguenti passi.
1) Esistenza del minimo. Si considera il problema di minimo in una opportuna classe C∼ più ampia di quella naturale, nel senso che contiene anche funzioni meno regolari di quelle di C. La scelta di C∼ va fatta in modo che abbia ancora senso il funzionale T e che si possa provare, sotto opportune ipotesi sulla lagrangiana L, che T ammette minimo in C∼.
2) Forma debole della equazione. Detto z tale minimo, si mostra che esso verifica, in una forma 'debole', l'equazione di Euler-Lagrange.
3) Regolarizzazione. Si prova che z appartiene effettivamente a C ed è una soluzione di EL in senso classico.
Per illustrare il procedimento descritto sopra, consideriamo il caso in cui T ha la forma [1]. Per evitare questioni tecniche, supporremo che L sia di classe C1.
Qui si può prendere C∼ come la classe delle funzioni assolutamente continue in [a,b] verificanti le condizioni al contorno u(a)=α, u(b)=β. È noto che le funzioni assolutamente continue sono derivabili quasi ovunque (rispetto alla misura di Lebesgue) e quindi ha senso considerare il funzionale T. Supponendo, per esempio, che L sia convessa in u′ e verifichi
[13] L(x,u,u′)≥c1∣u′∣2−c2 c1,c2>0
è possibile mostrare che T ha minimo z∈C∼ (in questo passaggio gioca un ruolo determinante il concetto di semicontinuità introdotto da Tonelli) e che z verifica
[14] formula
per ogni v assolutamente continua in [a,b] e tale che v(a)=v(b)=0. Questa è la forma debole dell'equazione [3] e z viene appunto detta soluzione debole.
Infine si dimostra, sotto qualche ulteriore restrizione sulla L, che z è di classe C1 e verifica la [3].
I risultati di Hilbert e Tonelli hanno dato un nuovo grande impulso alla ricerca nel calcolo delle variazioni. Ricordiamo il problema di determinare condizioni generali per la semicontinuità di T, anche nel caso vettoriale [7] o di integrali multipli [8], e il problema della regolarità, sul quale vanno ricordati i celebri teoremi di Ennio De Giorgi e John Nash.
Minimi e punti sella
Le ricerche di Hilbert e Tonelli ebbero un grande impatto anche nell'analisi nonlineare, anche se alcuni problemi tipicamente nonlineari erano già stati affrontati agli inizi del novecento da Aleksandr M. Liapunov e da Henri Poincaré nell'ambito della teoria della biforcazione.
I metodi diretti aprono infatti nuove prospettive per la ricerca nei problemi nonlineari di tipo variazionale poiché, come abbiamo già osservato, non solo i minimi ma tutti i punti critici di T sono soluzioni della equazione di Euler-Lagrange. E vi sono molti casi importanti in cui T non ha minimo, ovvero il minimo esiste ma dà origine a una soluzione banale, mentre le soluzioni non-banali sono dei punti sella di T. Oppure può accadere che sia naturale aspettarsi molte soluzioni della equazione di Euler-Lagrange, derivanti da molti punti critici di T. Per esempio, consideriamo il problema al contorno
[15] u″+λu+u3=0
x∈(a,b) u(0)=u(π)=0
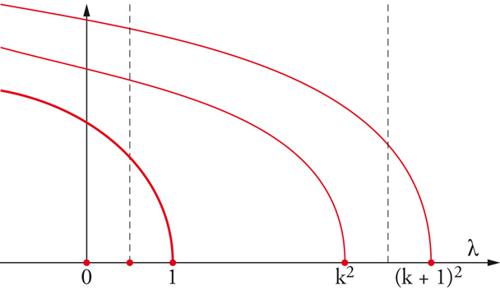
dove λ è un parametro reale. Un'analisi elementare nel piano delle fasi mostra che per ogni λ esso ha infinite (coppie di) soluzioni. Questo è evidenziato dal diagramma riportato nella fig. 1, dove le curve rappresentano famiglie di soluzioni che si biforcano da quella banale u≡0 in corrispondenza dei valori λk=k2, k=1,2,… La curva in grassetto che si dirama da λ1=1 rappresenta le soluzioni positive, quelle che si biforcano da λk=k2 rappresentano le soluzioni con k−1 zeri nell'intervallo aperto (0,π) e con derivata positiva in x=0. Le intersezioni delle rette tratteggiate λ=costante con le curve di biforcazione indicano le soluzioni del problema per quel valore del parametro. Per ogni λ〈1 esistono una soluzione positiva e infinite soluzioni che cambiano segno, per λ∈(k2,(k+1)2) soluzioni con un numero di zeri in (0,π) non minore di k. Ovviamente le soluzioni appaiono in coppia, perché se u è una soluzione anche −u lo è.
Il problema [15] è l'equazione di Euler-Lagrange del funzionale
[16] formula
definito sullo spazio di Sobolev H=H01,2(a,b), che coincide con lo spazio delle funzioni assolutamente continue in (a,b) tali che u(a)=u(b)=0. Si ha che infHT(u)=−∞ e supHT(u)=+∞. Infatti, fissata una qualunque u- ≢0 si ha
[17] formula
e questo implica che T(su)→−∞ per ∣s∣→∞. Inoltre, se prediamo per λ fissato una successione uλ,k di soluzioni della [15], è facile verificare che T(uλ,k)→+∞ per k→∞.
Un'analisi spettrale un po' più complicata mostrerebbe che nessuna di queste soluzioni è di minimo, nemmeno locale, fatta eccezione per la soluzione banale u=0 per λ〈1.
L'esempio riportato sopra è il prototipo di molti problemi variazionali nei quali non ci si può limitare alla ricerca del minimo di un funzionale ma occorre studiare l'esistenza di punti critici più generali, che saranno in generale dei punti di sella. Questo è l'obiettivo della teoria dei punti critici, che ha avuto un enorme sviluppo negli ultimi cento anni e attualmente rappresenta uno dei filoni di ricerca più attivi nell'analisi matematica.
Esistenza di punti sella
Inizieremo a esporre la teoria dei punti critici considerando il caso di un funzionale f in dimensione finita.
Sia M⊂ℝn una varietà definita dall'equazione g(x)=0, dove g: ℝn→ℝ è una funzione regolare e tale che ∇g(x)≠0 per ogni x∈M. Data f: ℝn→ℝ, vogliamo studiare l'esistenza dei punti critici di f vincolati su M, cioè degli x∈M tali che esiste λ∈ℝ per cui ∇f(x)=λ∇g(x) (metodo dei moltiplicatori di Lagrange). Se indichiamo con ∇Mf(x) il gradiente vincolato di f su M, definito come la proiezione di ∇f(x) sul piano tangente a M in x, si ha
[18] formula.
Possiamo allora anche dire che i punti critici di f vincolati su M sono gli x tali che ∇Mf(x)=0.
Un ruolo fondamentale per trovare tali punti è giocato dalle deformazioni. Se A è un sottoinsieme di M e η∈C(A,M), diremo che η è una deformazione (di A in M) se η è omotopa all'identità, cioè se esiste una omotopia h∈C([0,1]×A,M) tale che h(0,x)=x e h(1,x)=η(x), per ogni x∈A.
Per costruire deformazioni possiamo usare il flusso gradiente, cioè la soluzione ϕ(t,p)=ϕp(t) del problema di Cauchy
[19] formula.
Se M è compatta, ϕ è definita per ogni t≥0 e ϕp(t)∈M per ogni t≥0 e p∈M. Ovviamente, per ogni t_ fissato l'applicazione p→ϕ(t_,p) è una deformazione. Inoltre se calcoliamo f lungo una soluzione di [19] troviamo
[20] formula.
Poiché ϕ verifica [19], si deduce
[21] formula.
Quindi f è non crescente lungo il flusso gradiente e anzi se per t∈[0,t_] ϕp(t) non incontra punti critici di f esiste c>0 tale che ∣∇Mf(ϕp(t))∣2≥c e quindi f(ϕp(t_))≤f(p)−c. Da questo si può dedurre un lemma di deformazione:
Se M è compatta e nella striscia {x∈M tali che a≤f(x)≤b} non ci sono punti critici di f su M, allora il sottolivello Mb={x∈M tali che f(x)≤b} può essere deformato nel sottolivello Ma.
È evidente che se Mb è deformabile in Ma i due sottolivelli hanno le stesse proprietà topologiche (per es., sono entrambi omeomorfi a uno stesso insieme di M). Allora dal lemma di deformazione possiamo dedurre un primo criterio generale per l'esistenza di punti critici:
Se Mb è topologicamente differente da Ma, allora nella striscia {x∈M tali che a≤f(x)≤b} c'è almeno un punto critico.
Più in generale si dimostra:
Sia Γ una classe di sottoinsiemi di M stabili per deformazioni. Allora, posto
[22] formula,
esiste un punto critico x*∈M tale che f(x*)=c.
Per illustrare questi risultati faremo un esempio elementare ma interessante. Prendiamo come varietà M il toro bidimensionale in ℝ3 e come f la funzione f(x,y,z)=z. Il gradiente di f è il vettore (0,0,1) e quindi i punti critici di f vincolati su M sono i punti pi, i=1,2,3,4, dove tale vettore è ortogonale al toro raffigurato nella fig. 2. Posto ci=f(pi), i=1,…,4, prendiamo a〈b in modo che si abbia a〈c2〈b. I corrispondenti sottolivelli Ma ed Mb sono riportati nella fig. 3.Mb è topologicamente equivalente a un cilindro mentre Ma è equivalente a un disco. Poiché il cilindro non è topologicamente equivalente al disco, Mb non può essere deformato in Ma e quindi deve esserci un livello tra a e b che contiene un punto critico. Questo livello è c2 (fig. 2) e può essere ottenuto con il procedimento di min-max descritto prima: è sufficiente prendere come Γ la classe dei sottoinsiemi di M che non sono contraibili a un punto in M. Analogamente, preso a′〈c1 si ha Ma′=→ e perciò deve esserci un livello critico al di sotto di a: questo è il livello di minimo c1. In modo simile si ottiene il livello di massimo c4. Per trovare c3 occorrerebbe fare un max-min, invece di un min-max. In generale, si può dimostrare che una generica funzione regolare f ha sul toro almeno tre punti critici: il massimo e il minimo assoluti e un punto sella che si trova con un min-max. Inoltre esistono funzioni che hanno esattamente tre punti critici sul toro.
Sviluppando queste tecniche si possono ottenere risultati molto interessanti e di grande eleganza. Ci limitiamo a citare un risultato di Lazar Lusternik e Lev Schnirelman secondo cui ogni funzione regolare e pari ha almeno n coppie di punti critici sulla sfera unitaria di ℝn.
La teoria di Morse
La teoria di Morse (da Marston Morse, che la ideò) è un metodo brillante e preciso per trovare i punti critici di un funzionale f di classe C2 su una varietà M mediante proprietà topologiche di M. Esso richiede che f abbia solo punti critici p non degeneri, cioè tali che la matrice hessiana D2fM(p) di f ristretta a M sia invertible. Una f con tale proprietà è chiamata funzione di Morse.
Se p è un punto critico non degenere, il suo indice di Morse è, per definizione, la dimensione del sottospazio di ℝn dove la matrice D2fM(p) è definita negativa. Se k è l'indice di p si può provare che in un intorno di p esiste un sistema di coordinate (y1,…,yn) tale che, rispetto a queste coordinate, si ha
[23] f(y)=f(p)−y12−…−yk2+y2k+1+…+yn2.
È questo il celebre lemma di Morse. Esso descrive in modo preciso la struttura dei sottolivelli Mc, per c vicino a f(p), e permette di ottenere mediante delle deformazioni opportune le diseguaglianze di Morse. Per enunciarle, occorre far uso dei gruppi di omologia singolare Hk(M).
Posto βk=Rank(Hk(M)) (numeri di Betti di M) e indicato con Ck il numero di punti critici di f su M di indice k, si ottengono le diseguaglianze di Morse
[24] formula.
Per esempio, i numeri di Betti del toro in ℝ2 sono β0=1, β1=2, β2=1. Si può dedurre che ogni funzione di Morse ha 4 punti critici sul toro, uno di indice 0 (il minimo assoluto), uno di indice 2 (il massimo assoluto) e due punti sella di indice 1. È chiaro come questo risultato sia più preciso di quello visto prima (infatti ora siamo in grado di trovare simultaneamente sia p1 che p2). Naturalmente, occorre supporre che f sia di Morse: si possono altrimenti costruire delle funzioni che hanno solo 3 punti critici sul toro in ℝ2. Inoltre, indicata con χ(M)=∑j(−1)jβj(M) la caratteristica di Euler-Poincaré di M, si trova
[25] formula.
Osserviamo come le diseguaglianze di Morse e la formula [25] possano essere usate anche in senso inverso, cioè per valutare i numeri di Betti o per calcolare la caratteristica di Euler-Poincaré di una varietà. Basterà costruire una opportuna funzione di Morse di cui si conoscono i punti critici, e quindi i numeri Ck. Se per esempio nel caso del toro prendiamo f(x,y,z)=z si ha C0=1, C1=2 e C2=1. Usando le diseguaglianze di Morse si ricavano i numeri di Betti, mentre la [25] permette di calcolare la caratteristica di Euler-Poincaré: χ(M)=1−2+1=0.
Il caso non compatto
Nelle sezioni precedenti abbiamo sempre supposto che M sia compatta ma è naturale chiedersi cosa si può ottenere nel caso non compatto. Per semplicità considereremo il caso M=ℝn: il seguente esempio elementare mostra come i risultati ottenuti sopra non siano più validi. Consideriamo la funzione f : ℝ→ℝ, definita ponendo f(x)=(1+x2)−1. Prendendo a〈0〈b〈1 si ha che Mb=(−∞,−β]∪[β,+∞), dove β soddisfa (1+β2)−1=b, mentre Ma=→.
Ma, sebbene Mb non sia topologicamente equivalente a Ma, f non ha punti critici a livelli minori di 1.
Una condizione che sostituisce la compattezza e permette di riottenere il lemma di deformazione è la seguente, introdotta da Richard S. Palais e Steven Smale (PSc): ogni succesione tale che f(xk)→c e ∇f(xk)→0 ha una sottosuccessione convergente xk→p.
Naturalmente, p è un punto critico per f. In pratica basterà provare che ogni successione per cui f(xk)→c e ∇f(xk)→0 è limitata. Nell'esempio precedente la condizione PSc non è verificata al livello c=0.
Nel caso non compatto è anche naturale considerare funzionali indefiniti, cioè tali che infℝnf=−∞ e supℝnf=+∞. La situazione che vogliamo affrontare è quella in cui f ha un minimo locale, per esempio in x=0. Possiamo pensare a un punto sul fondo di una valle circondata da montagne, dalla quale vogliamo uscire attraverso un passo montano. Per ogni percorso che parte da x=0 e finisce fuori dalla valle, sceglieremo quello per cui il massimo di f(γ(t)) è il più piccolo possibile. Per formalizzare questo discorso, supponiamo che esistano r,α>0 tali che:
1) f(x)≥α per ogni x∈ℝn tale che ∣x∣=r.
2) Esiste x1∈ℝn tale che ∣x1∣>r e f(x1)〈α.
Consideriamo la classe Γ delle curve γ: [0,1]→ℝn tali che γ(0)=0 e γ(1)=x1 e mediante Γ definiamo il livello
[26] formula.
Si può dimostrare che, se vale la condizione PSc, allora c è un livello critico per f e cioè esiste p∈ℝn tale che f(p)=c e ∇f(p)=0. Per escludere che il punto trovato sia 0, osserviamo che se γ∈Γ parte da x=0 e termina in x1, con ∣x1∣>r, tale cammino interseca la sfera ∣x∣=r in un punto zγ. Allora, tenuto conto della (1), si avrà che
[27] formula.
Poiché questa diseguaglianza è valida per ogni γ∈Γ, si deduce che c≥α>0 e quindi p non coincide col punto critico banale x=0. In conclusione, si ha:
Se f verifica (1) e (2) e se vale la PSc, con c dato da [26], allora f ha un punto critico p≠0 tale che f(p)=c.
Questa è la versione finito dimensionale di un risultato più generale (si veda anche la sezione seguente). Il punto p viene chiamato punto di passo montano.
Si può anche dimostrare che se p è non degenere, allora è un punto sella con indice di Morse uguale a 1.
Il seguente esempio in ℝ2 mostra che l'ipotesi di compattezza, cioè la validità della PSc, non può essere eliminata. Per (x,y)∈ℝ2, poniamo f(x,y)=x2+(1−x)3y2. È facile verificare che la condizione (1) è soddisfatta con r=1/2 e α=1/32 . Inoltre, se prendiamo il punto (2,2) si ha che f(2,2)=0 e quindi vale anche (2). Tuttavia, l'unico punto critico di f è l'origine: ∇f=0 diventa infatti il sistema
[28] formula
il quale ha solo la soluzione (x,y)=(0,0) come si vede immediatamente. Il lettore può verificare che in questo caso c=1 ma la condizione PSc al livello c=1 non è soddisfatta.
La teoria dei punti critici negli spazi funzionali
Come abbiamo osservato, i problemi variazionali hanno come incognita una funzione e quindi sono ambientati in modo naturale negli spazi funzionali. Occorre perciò estendere i risultati esposti nel paragrafo precedente a questi spazi. La differenza principale rispetto al caso euclideo è che si tratta di spazi di dimensione infinita.
Per maggiore semplicità, tratteremo un caso particolare ma significativo. Consideriamo uno spazio vettoriale H dove è definito un prodotto scalare (u∣v), che induce una norma ∣∣u∣∣2=(u∣u). A sua volta la norma permette di definire in modo naturale una distanza d ponendo d(u,v)=∣∣u−v∣∣, alla quale corrisponde una nozione di convergenza: un→u se e solo se ∣∣un−u∣∣→0. Se H è completo rispetto a questa convergenza è detto spazio di Hilbert. Per esempio, se Ω è un aperto limitato di ℝn lo spazio L2(Ω) delle funzioni a quadrato sommabile (secondo Lebesgue) in Ω è uno spazio di Hilbert rispetto al prodotto scalare (u∣v)=∫Ωu(x)v(x)dx.
Un funzionale su H è una applicazione J: H→ℝ (J potrebbe anche essere definito su un sottoinsieme di H, ma qui non considereremo questo caso). Dato u∈H, diremo che J è differenziabile in u se esiste un elemento di H, che indicheremo col simbolo ∇J(u), tale che
[29] formula.
∇J(u) è il gradiente di J. Se H=ℝn, ∇J è l'usuale vettore gradiente le cui componenti sono le derivate parziali di J.
Se J è differenziabile, un punto critico di J è uno z∈H tale che ∇J(z)=0, cioè (∇J(z)∣v)=0 per ogni v∈H. In generale, i punti critici di un funzionale J su uno spazio di Hilbert H verificano l'equazione (∇J(u)∣v)=0 per ogni v∈H, che è in pratica la forma debole della equazione di Euler-Lagrange.
Vediamo con un esempio quale è il procedimento che viene usualmente seguito. Dati un aperto limitato Ω⊂ℝn e una funzione ψ: Ω×ℝ→ℝ, consideriamo il problema di Dirichlet nonlineare
[30] formula,
dove Δ=∑∂2/∂xi2 è l'operatore di Laplace in ℝn. Il corrispondente funzionale è dato da
[31] formula.
Ovviamente, è nella forma ∫ΩL(x,u,∇u)dx con L=∣∇u∣2/2−Ψ(x,u). Lo spazio naturale su cui cercare i punti critici di J è lo spazio di Sobolev H=W01,2(Ω) delle funzioni u∈L2(Ω) che hanno derivate, nel senso delle distribuzioni, in L2(Ω) e si annullano al bordo di Ω. H è uno spazio di Hilbert rispetto al prodotto scalare (u∣v)=∫Ω∇u∙∇vdx. Inoltre è noto che W01,2(Ω)⊂Lq(Ω) non appena 1≤q≤2*, dove 2*=2n/(n−2) se n>2 e 2*=+∞ altrimenti. In base a queste considerazioni, possiamo concludere che J è ben definito su W01,2(Ω) a patto di supporre che Ψ(x, u)≈∣u∣p per ∣u∣→∞, con p≤2*. Per tali valori di p si vede anche che J è regolare. Il gradiente di J è definito dalla relazione
[32] formula
e un punto critico z di J verifica (∇J(z)∣v)=0 per ogni v∈W01,2(Ω). Questa è precisamente la forma debole della equazione di Euler-Lagrange, cioè la [14]. Per regolarizzazione, si può poi dimostrare che se ψ è hölderiana allora z è di classe C2. Integrando per parti si ottiene
[33] formula.
Poiché tale relazione è verificata per ogni v∈W01,2(Ω), si deduce che z risolve il problema [30] (la condizione al bordo è automaticamente soddisfatta perché z appartiene a W01,2(Ω)).
In modo analogo si può estendere la nozione di punto critico vincolato. Per esempio, i punti critici vincolati di J sulla sfera hilbertiana S={u∈H tali che ∣∣u∣∣=1} sono le soluzioni del problema agli autovalori ∇J(u)=λu, con u∈S.
Teoremi di esistenza
I risultati discussi in precedenza nel caso euclideo possono essere estesi agli spazi di Hilbert. Naturalmente dovremo supporre che valga la condizione di Palais-Smale PSc, che riscriviamo con le notazioni attuali: ogni successione uk∈H tale che J(uk)→c e ∇J(uk)→0 ha una sottosuccessione convergente uk→u*.
È opportuno osservare esplicitamente che, a differenza del caso euclideo, per verificare la PSc non basta più mostrare che uk è limitata. Infatti, se H è infinito, dimensionale i dischi {u∈H tali che ∣∣u∣∣≤c} non sono compatti nella topologia indotta dalla norma (topologia forte) ma solo in quella debole: a meno di sottosuccessioni, (uk−u*∣v)→0 per ogni v∈H. Per passare dalla convergenza debole a quella forte occorre qualche ulteriore argomento.
Se vale la condizione PSc, si possono estendere senza problemi il risultati enunciati in precedenza in ℝn. Ci limitiamo qui ad enunciare due teoremi particolarmente importanti. Il primo, che estende il corrispondente risultato di Lusternik e Schnirelman, afferma:
Supponiamo che H sia uno spazio di Hilbert separabile di dimensione infinita e che J∈C1(H,ℝ) verifichi le seguenti condizioni: (a) J(u)〈0, ∀u≠0; (b) ∇J(u)≠0, ∀u≠0; (c) ∇J è compatto; (d) J(u)=J(−u).
Allora J ha infiniti punti critici sulla sfera S.
Qui si usano le condizioni (a-b-c-d) per provare che J verifica sulla sfera la condizione PSc per ogni c〈0.
Il secondo risultato che vogliamo enunciare è il teorema del passo montano.
Supponiamo che J∈C1(H,ℝ) verifichi J(0)=0 e J(u)≥α per ogni u∈H con ∣u∣=r e che esista u1∈H con ∣u1∣>r e J(u1)〈α. Consideriamo il livello
[34] formula
dove Γ={γ∈C([0,1],H) tali che γ(0)=0, γ(1)=u1}. Se valgono le ipotesi precedenti e PSc, allora esiste z∈H tale che J(z)=c>0 e ∇J(z)=0.
Si osservi come non si fa nessuna ipotesi sul fatto che J sia inferiormente o superiormente limitato. Infatti, può accadere (si veda l'esempio seguente) che risulti infHJ=−∞ e supHJ=+∞.
Vediamo come si applica quest'ultimo teorema al problema [30]. Prenderemo per semplicità ψ(x,u)=∣u∣p−2u, 2〈p≤2*, e dunque
[35] formula
Poiché p>2, si verifica facilmente che valgono (a) e (b). Per quanto riguarda la PSc, prima si deduce da J(uk)→c>0 e ∇J(uk)→0 che uk è limitata in W01,2(Ω) e successivamente si usa il fatto che l'immersione di W01,2(Ω) in Lq(Ω) è compatta non appena q〈2*. Segue allora che, se p〈2*, dalla limitatezza di uk si può dedurre la convergenza forte di uk a meno di sottosuccessioni.
Possiamo quindi applicare il teorema del passo montano che assicura l'esistenza di un punto critico u≠0 di J, in modo che l'equazione −Δu=∣u∣p−2u ha una una soluzione non banale in W01,2(Ω) non appena 2〈p〈2*. Osserviamo che, in base a una identità di Stanislav I. Pohozaev, il problema −Δu=∣u∣2*−2u, u∈W01,2(Ω), ha solo la soluzione banale u≡0.
Più in generale, possiamo considerare problemi del tipo
[36] formula.
In dimensione n=1 questo è nient'altro che il problema [15]. La differenza rispetto al caso precedente sta nel fatto che per λ grande il funzionale
[37] formula
non verifica più l'ipotesi (a). Tuttavia sono stati anche sviluppati dei teoremi di esistenza di punti critici, più generali del passo montano (teoremi di linking), che permettono di studiare anche questo caso ottenendo risultati che estendono in modo completo quelli descritti nel paragrafo 3 e riportati nella fig. 1.
Il caso dell'esponente critico
Il caso in cui p=2* (esponente critico) presenta dei nuovi fenomeni ed è stato affrontato per la prima volta da Haim Brezis e Louis Nirenberg, che hanno studiato l'esistenza di soluzioni positive per il problema
[38] formula.
Indichiamo con λ1 il più piccolo valore di λ∈ℝ per cui il problema −Δu=λu, con u=0 per x∈∂Ω, ha soluzione. Brezis e Nirenberg hanno dimostrato il seguente risultato:
Se n≥4 il problema [38] ha una soluzione positiva per tutti i λ∈]0,λ1[.
Se n=3 esiste λ*∈[0,λ1[ tale che [38] ha una soluzione positiva se e solo se λ∈[λ*,λ1].
L'interesse non sta solo nel risultato in se stesso ma anche nel metodo dimostrativo, ripreso da molti altri autori. La difficoltà sta nel fatto che, a causa della presenza dell'esponente critico, non si possono più utilizzare gli argomenti prima accennati per provare la condizione di Palais-Smale (invece le ipotesi geometriche del teorema del passo montano sono verificate). Per superare questo ostacolo si prova:
1) La PSc vale per c〈Sn/2/n, dove S=inf{∣∣u∣∣2 tali che u∈W01,2(Ω), ∫Ω∣u∣2*=1} è la migliore costante dell'immersione di W01,2(Ω) in L2*(Ω) (ricordiamo che S non dipende da Ω).
2) Se λ verifica le condizioni del teorema, allora il livello di passo montano è minore di Sn/2/n.
Si deduce allora facilmente che c è un livello critico, nel senso che esiste un punto critico del corrispondente funzionale a livello c. Questo punto critico è la soluzione cercata.
Un risultato qualitativo
Terminiamo questa sezione enunciando un risultato qualitativo di grande eleganza, dovuto a Basilis Gidas, Wei-Ming Ni e Nirenberg. Mediante l'uso del metodo del moving plane esso stabilisce quanto segue:
Sia B={x∈ℝn tali che ∣x∣〈1} e ψ∈C1([0,+∞),ℝ). Ogni soluzione positiva u∈C2(B−) di −Δu=ψ(u) in B e u=0 sul bordo ∂B è radiale in B. Inoltre ∂u/∂r〈0.
L'interesse del risultato sta nel fatto che esso vale per una qualunque nonlinearità ψ(u).
Sviluppi recenti
A partire dal lavoro di Brézis e Nirenberg si è andato sviluppando un grande interesse per i problemi variazionali nei quali non è soddisfatta la condizione di Palais e Smale.
In molti di questi problemi PSc non vale perché essi sono invarianti rispetto a un gruppo non compatto di isometrie e il recupero della compattezza avviene per la presenza di un termine che rompe la simmetria. In una serie di articoli Pierre-Louis Lions ha sviluppato una teoria abbastanza generale (il metodo di concentrazione-compattezza) per studiare questi fenomeni; per semplificare l'esposizione preferiamo qui esporre alcuni casi tipici di particolare interesse.
Problemi ellittici in Rn
Problemi ellittici su tutto ℝn intervengono spesso in fisica. Per esempio, consideriamo l'equazione di Klein-Gordon non lineare
[39] formula,
dove ϕ(t,x) è una funzione a valori complessi. Cerchiamo soluzioni del tipo ϕ(t,x)=e−iωtu(x), con ω∈ℝ e u(x)∈ℝ (onde stazionarie). Sostituendo in [39], si trova per u l'equazione
[40] formula,
a cui si aggiunge la condizione u∈W1,2(ℝ) per ottenere soluzioni di energia finita.
Per avere un'idea dei risultati che si possono ottenere, discutiamo il problema modello
[41] −Δu+u=a(x)p−1 u>0, u∈W1,2(ℝ),
dove 2〈p〈2*. Le soluzioni di [41] sono i punti critici del funzionale
[42] formula.
È facile vedere che J verifica le ipotesi geometriche del teorema del passo montano ma non la PSc. Se a(x) è costante, per esempio a(x)≡1, è noto che [41] ha una unica soluzione radiale che indicheremo con U. Il problema è invariante rispetto al gruppo delle traslazioni x→x+ξ e quindi anche ogni U(x+ξ) è soluzione di [41]. Poiché, ovviamente, presa una successione ξk con ∣ξk∣→∞ la successione Uk(x)=U(x+ξk) non è compatta in W1,2(ℝn), la condizione PSc non è verificata. Il coefficiente a(x) rompe però questa invarianza e si tratta di vedere sotto quali ipotesi si recupera la PSc. Usando il metodo di concentrazione-compattezza di Lions si può dimostrare, in analogia con quanto visto per il problema con l'esponente critico, che PSc vale per c al di sotto di una soglia critica c*. Se lim∣x∣→∞a(x)=1 e a(x)>1, si vede che J verifica la PSc al livello di passo montano c. Più delicato è il caso in cui a〈1. È stato provato da Abbas Bahri e Lions che se esistono a0,δ>0 tali che a(x)>1−a0e−(2+δ)∣x∣ per ∣x∣ sufficientemente grande allora [41] ha una soluzione.
Concludiamo enunciando un teorema di non-esistenza, dovuto a Gidas e Joel Spruck:
Sia u∈C2(ℝn) una soluzione non negativa dell'equazione −Δu=up, con p−1〈2* e n≥3, allora u≡0.
Equazioni di Schrödinger non lineari
Quando il problema è di tipo perturbativo la mancanza di compatezza può essere superata mediante argomenti specifici. Ci limitiamo qui al caso dell'equazione di Schrödinger non lineare
[43] formula,
che interviene in meccanica quantistica (ℏ è la costante di Planck). Se cerchiamo onde stazionarie del tipo ϕ(t,x)=eiℏ−1λtu(x), troviamo l'equazione
[44] formula.
Per la transizione dalla meccanica classica a quella quantistica è particolarmente interessante studiare l'esistenza e il comportamento degli stati semiclassici, cioè delle soluzioni uℏ>0 della [44] per ℏ→0. Con il cambio di variabile x→ℏx, essa diventa ∂2u/∂x2+λu+V(ℏx)u=u3, forma che mette in evidenza come, per ℏ piccolo, possa essere studiata come perturbazione del problema ∂2u/∂x2+λu+V(0)u=u3. Il fenomeno più interessante riguardo gli stati semiclassici è la concentrazione delle soluzioni: diremo che uℏ si concentra in x0 per ℏ→0 se uℏ(x)→0 quando ℏ→0, uniformemente per x≠x0.
Un risultato tipico è il seguente, ottenuto da Andreas Floer e Alan Weinstein:
Supponiamo che V∈C2(ℝ) sia tale che ∣∣V∣∣C2(ℝ)≤cost. e che λ+infℝV>0. Se x0 è un punto critico di V non degenere, allora, per ℏ sufficientemente piccolo, [44] ha una soluzione uℏ>0 che si concentra in x0 quando ℏ→0.
Viceversa, se [44] ha per ℏ→0 una soluzione uℏ che si concentra in x*, allora V′(x*)=0.
Lo studio degli stati semiclassici dell'equazione [44] è proseguito ottenendo varie estensioni del risultato precedente ed è ancora oggetto di indagine estremamente vivace.
Problemi di geometria differenziale
Anche la geometria differenziale è una fonte di problemi ellittici non lineari di tipo variazionale. L'esempio tipico è un risultato di Poincaré che prova l'esistenza di metriche conformi tali che una varietà compatta di dimensione 2 abbia curvatura gaussiana costante. Per avere un'idea della natura di tali questioni e delle difficoltà che sorgono, considereremo brevemente il problema seguente. Data la sfera n-dimensionale Sn con la metrica standard g0, ci si chiede se è possibile trovare una metrica g a essa conformemente equivalente, cioè tale che g=ϱg0 per qualche ϱ(x)>0, in modo che Sn munita della nuova metrica g abbia per curvatura scalare una funzione R(x) assegnata. Considereremo il caso n≥3 e R>0. Ponendo ϱ=u4/(n−2) e usando la proiezione stereografica π, il problema si riduce, per n≥3, a trovare una soluzione positiva dell'equazione su ℝn
[45] formula
tale che ∫ℝn∣∇u∣2〈∞. Se R∼≡1, il problema precedente è invariante non solo per traslazioni (perché è posto su tutto ℝn) ma anche per dilatazioni x→μx con μ>0 poiché la non lineraità è critica (si noti che (n+2)/(n−2)=2*−1). Questo rende lo studio di [45] molto più delicato e difficile rispetto a quanto visto per le equazioni su ℝn con esponente minore di quello critico.
Sono state trovate condizioni necessarie per l'esistenza dovute a Jerry L. Kazdan e Frank W. Warner, mentre condizioni sufficienti sono state date da Bahri, Sung-Yung A. Chang, Jean-Michel Coron, Yan Yan Li, Paul C. Yang e altri. Per esempio, se n=3 si può dimostrare l'esistenza di una soluzione positiva di [45] sotto le seguenti condizioni:
a) R∼ è una funzione di Morse e ha un numero finito di punti critici x1,…,xk.
b) Per ogni j=1,…,k si ha ΔR∼(xj)≠0.
c) Indicato con mj l'indice di Morse di xj, si ha
[46] formula.
Negli ultimi anni la teoria dei punti critici è stata usata anche per studiare altri problemi di geometria conforme, che coinvolgono operatori differenziali di ordine 4 o completamente non lineari.
Bibliografia
Ambrosetti 1998: Ambrosetti, Antonio, Metodi variazionali in analisi nonlineare, in: Enciclopedia del Novecento, Roma, Istituto della Enciclopedia Italiana, X, Suppl. II, 1998, pp. 18-25.
Ambrosetti, Prodi 1989: Ambrosetti, Antonio - Prodi, Giovanni, Analisi nonlineare, in: Enciclopedia del Novecento, Roma, Istituto della Enciclopedia Italiana, VIII, 1989, pp.15-28.
Ambrosetti, Malchiodi 2005: Ambrosetti, Antonio - Malchiodi, Andrea, Perturbation methods and semilinear el-_liptic problems on Rn, Basel-Boston, Birkhäuser, 2005.
Ambrosetti, Malchiodi 2006: Ambrosetti, Antonio -Malchiodi, Andrea, Nonlinear analysis and semilinear elliptic problems, Cambridge, Cambridge University Press, 2006.
Ambrosetti, Rabinowitz 1973: Ambrosetti, Antonio - Rabinowitz, Paul H., Dual variational methods in critical point theory and applications, "Journal of functional analysis", 14, 1973, pp. 349-381.
Buttazzo 1998: Buttazzo, Giuseppe - Dal Maso, Gianni - De Giorgi, Ennio, Calcolo delle variazioni, in: Enciclopedia del Novecento, Roma, Istituto della Enciclopedia Italiana, XI, Suppl. II, 1998, pp. 832-848.
Dal Maso 2003: Dal Maso, Gianni, Calcolo delle variazioni, in: Storia della scienza, Roma, Istituto della Enciclopedia Italiana, 2003, IX, pp. 293-301.
Lions 1977: Lions, Jacques-Louis, Equazioni funzionali, in: Enciclopedia del Novecento, Roma, Istituto della Enciclopedia Italiana, XII, pp. 709-719.
Lions 1984: Lions, Pierre-Louis, The concentration-compactness principle in the calculus of variation. The locally compact case 1 & 2, "Annales de l'Institut Henri Poincaré (C) Analyse non linéaire", 1/2-1/4, 1984, pp. 109-145 e 223-283.
Lions 1985: Lions, Pierre-Louis, The concentration-compactness principle in the calculus of variation. The locally compact case 1 & 2, "Revista matemática iberoamericana", 1/1-1/2, 1985, pp. 541-597 e 45-121.