angoli associati (rispetto a due rette tagliate trasversalmente)

angoli associati (rispetto a due rette tagliate trasversalmente)

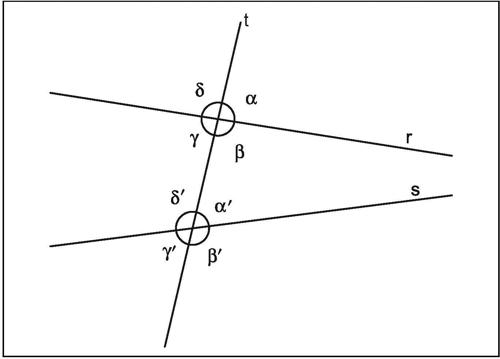
angoli associati (rispetto a due rette tagliate trasversalmente) particolari coppie di angoli tra gli otto formati da due rette intersecate da una terza retta (si dice allora che le due rette sono «tagliate» da una trasversale). Tali angoli assumono particolare rilievo nella geometria del piano nel caso in cui le due rette tagliate dalla trasversale sono parallele. Forniscono infatti utili criteri di parallelismo tra rette.

Angoli alterni

Coppie di angoli, tra gli otto angoli formati da due rette r e s tagliate dalla trasversale t, che non hanno vertici in comune e appartengono a semipiani opposti rispetto a t. Si dicono alterni interni se appartengono all’angolo convesso individuato dalle due rette r e s oppure alla striscia di piano da esse individuata nel caso siano parallele; si dicono alterni esterni se non vi appartengono. Due angoli alterni interni (oppure esterni) sono tra loro congruenti, hanno cioè la stessa ampiezza, se e solo se le due rette r e s sono parallele.

Angoli coniugati

Coppie di angoli, tra gli otto angoli formati da due rette r e s tagliate dalla trasversale t, che non hanno vertici in comune e appartengono a uno stesso semipiano rispetto alla trasversale t. Si dicono coniugati interni se appartengono all’angolo convesso individuato dalle due rette r e s oppure alla striscia di piano da esse individuata nel caso siano parallele; si dicono coniugati esterni se non vi appartengono. Due angoli coniugati interni (o esterni) sono supplementari se e solo se le rette r e s sono parallele.

Angoli corrispondenti

Coppie di angoli, tra gli otto angoli formati da due rette r e s tagliate da una trasversale t, che non hanno vertici in comune, appartengono allo stesso semipiano rispetto alla trasversale t e sono disposti l’uno internamente e l’altro esternamente rispetto all’angolo convesso formato dalle rette r e s oppure alla striscia di piano da esse individuata nel caso siano parallele. Due angoli corrispondenti hanno la stessa ampiezza se e solo se le rette r e s sono parallele.