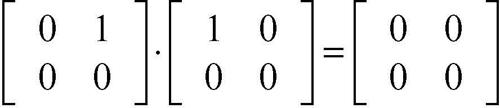annullamento del prodotto, legge di
annullamento del prodotto, legge di
annullamento del prodotto, legge di proprietà dei numeri reali per la quale, se il prodotto di due numeri è nullo, allora uno dei due fattori è necessariamente uguale a 0. Tale proprietà può essere utilizzata per risolvere equazioni polinomiali anxn + ... + a0 = 0 quando il polinomio è scomponibile in fattori. Per esempio, l’equazione polinomiale x4 − 16 = 0 può essere riscritta come (x − 2)(x + 2)(x2 + 4) = 0 e, proprio in virtù della legge di annullamento del prodotto, può essere spezzata nelle equazioni (di grado minore) x − 2 = 0 oppure x + 2 = 0 oppure x2 + 4 = 0. In generale, la legge di annullamento del prodotto esprime la proprietà dell’operazione moltiplicativa di un anello A così enunciabile: se a e b sono elementi di A tali che ab = 0, allora vale necessariamente a = 0 oppure b = 0. In un anello A è soddisfatta tale legge se e solo se A è privo di divisori dello zero, nel qual caso esso viene detto anello di integrità. Tale legge vale in ogni campo, nell’anello degli interi e nell’anello dei polinomi a coefficienti in un anello. Non vale invece, per esempio, nell’anello delle matrici quadrate a coefficienti in un campo. Infatti: