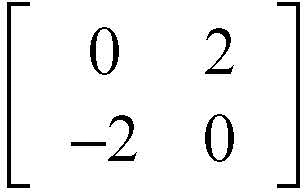antisimmetria

antisimmetria

antisimmetria termine usato con diversi significati in diversi ambiti dell’algebra.

☐ Una relazione ρ su un insieme A si dice antisimmetrica se vale l’implicazione seguente, dove a e b sono arbitrari elementi di A: se a ρ b e b ρ a allora a = b. Si dice anche che la relazione gode della proprietà antisimmetrica. Una definizione logicamente equivalente è la seguente: se a ρ b e a ≠ b allora non (b ρ a). Tutte le relazioni d’ordine (quale per esempio la relazione «essere minore o uguale» nell’insieme dei numeri reali R, indicata con ≤, o la relazione d’ordine stretto «essere minore», indicata con <) sono per definizione antisimmetriche.

☐ Una matrice quadrata M si dice antisimmetrica se coincide con l’opposta della sua trasposta, cioè se M =−M ^T, dove l’apice ^T indica l’operatore di trasposizione sull’algebra delle matrici. Per esempio la matrice quadrata di ordine due

è antisimmetrica. Una matrice quadrata antisimmetrica non singolare ha necessariamente ordine pari.

☐ La nozione di antisimmetria definita per una matrice, essendo invariante per trasposizione, può essere riformulata in modo equivalente in termini di forme bilineari su uno spazio vettoriale V su un campo K: una forma bilineare ƒ: V × V → K si dice antisimmetrica se, per ogni coppia di vettori v e w appartenenti a V, risulta ƒ(v, w) = −ƒ(w, v). In dimensione finita, una forma bilineare è antisimmetrica se e solo se lo è la matrice quadrata associata.