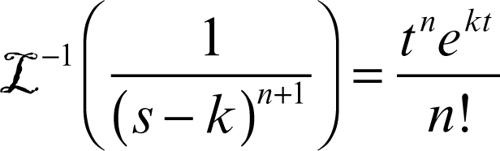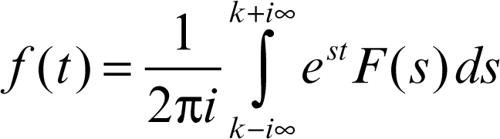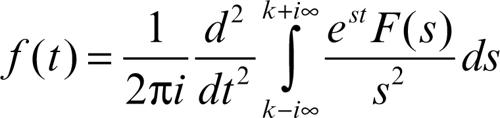Laplace, antitrasformazione di

Laplace, antitrasformazione di

Laplace, antitrasformazione di trasformazione inversa della trasformazione ℒ di Laplace. Essendo quest’ultima biunivoca, se è nota F(s) = ℒ(ƒ(t)) è possibile ricavare la funzione generatrice ƒ(t) = ℒ⁻¹(F(s)). Tale funzione ƒ(t) è detta antitrasformata di Laplace della funzione F(s). Nelle applicazioni si incontrano spesso i seguenti casi:

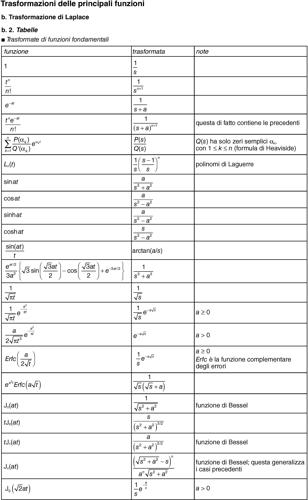
• se F(s) è una funzione razionale, la si decompone in fratti semplici le cui funzioni generatrici sono immediate. Infatti per n ≥ 0 si ha

• se F(s) è il prodotto di due trasformate, ƒ(t) è la convoluzione delle corrispondenti funzioni generatrici;

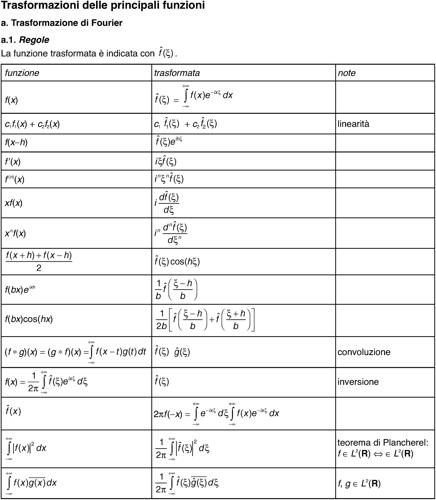
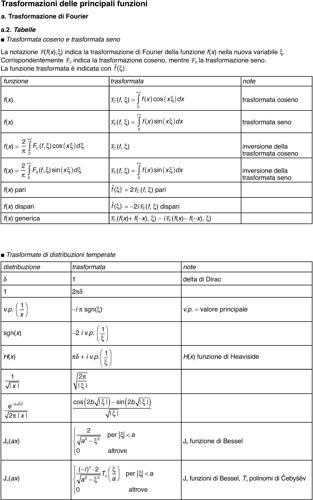
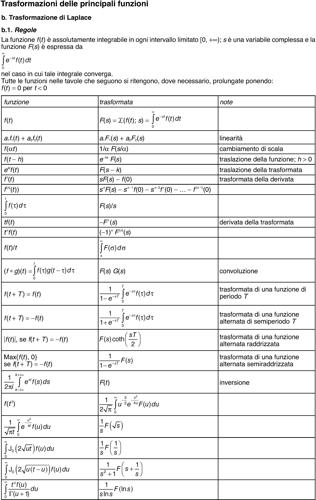
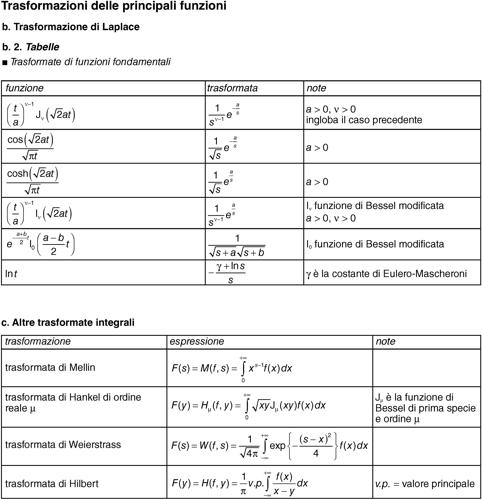
• in altri casi è in genere possibile trovare la funzione ƒ(t) in una apposita tabella.

Quando ciò non sia possibile, si può ricorrere a una formula generale che fornisce l’antitrasformata ƒ(t) mediante un integrale nel campo complesso. Considerata innanzitutto la trasformata bilatera

si scrive il numero complesso s come s = u + iv. È allora

e quindi, fissato u = k nell’intervallo (a, b) di assoluta convergenza, si può considerare F(s) come la trasformata di Fourier della funzione e^−ktƒ(t). La formula di inversione della trasformata di Fourier fornisce quindi

e quindi

(formula di Riemann-Fourier). L’integrale è valutato lungo la retta u = k del piano complesso, ma il suo valore non dipende da k, nell’intervallo indicato. Nei punti di salto di ƒ(t) l’integrale assume il valore (ƒ(t ⁺) + ƒ(t ⁻))/2. Naturalmente il caso della trasformata unilatera si riduce a quello ora indicato prolungando ƒ(t) con 0 per t < 0.

Nel caso in cui a =+∞, è possibile ottenere una formula di validità generale scrivendo

valida per k > max{λ, 0}, che fornisce ƒ(t) tranne eventualmente un insieme di misura nulla. Si vedano le tavole delle trasformazioni delle principali funzioni.