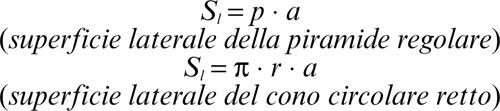apotema

apotema

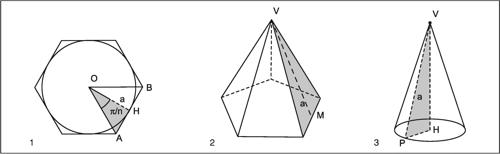
apotema segmento utilizzato per il calcolo delle aree di alcune figure geometriche. Nella geometria piana, l’apotema di un poligono regolare è il segmento di perpendicolare condotto dal centro del poligono a un suo lato; coincide con il raggio del cerchio inscritto nel poligono. Nella geometria solida il termine ha diverso significato. L’apotema di una piramide regolare è il segmento che va dal vertice al punto medio di un lato del poligono di base, cioè l’altezza di ciascuno dei triangoli della superficie laterale; l’apotema di un cono circolare retto è invece il segmento che congiunge il vertice del cono con un punto qualunque della circonferenza di base, cioè l’ipotenusa del triangolo rettangolo che ruotando intorno all’altezza genera il cono. In base alla definizione data, l’apotema di un poligono regolare di n lati è l’altezza di ciascuno degli n triangoli isosceli in cui il poligono viene suddiviso, congiungendo il centro del poligono con ciascuno dei suoi vertici. L’area del poligono è data pertanto da

cioè A_n = p ⋅ a, avendo indicato con l_n la lunghezza del lato, con a la lunghezza dell’apotema e con p il semiperimetro del poligono. Apotema e lato di un poligono regolare sono legati da una relazione di proporzionalità. Indicando con A un vertice di un poligono regolare di n lati e con H il punto su un lato di estremo A su cui cade l’apotema, si ha

cioè:

Il numero

dipende solo da n (numero dei lati); esso è pertanto una costante caratteristica di ogni tipo di poligono regolare ed esprime il rapporto tra apotema e lato. Nel calcolo ci si avvale di valori approssimati degli ƒ_n, che prendono il nome di numeri fissi. Per esempio: ƒ₅ = 0,688..., ƒ₆ = 0,866..., ƒ₇ = 1,038..., ƒ₈ = 1,207... Moltiplicando la misura del lato per il numero fisso corrispondente si ottiene la misura dell’apotema.

Per quanto riguarda la piramide regolare e il cono circolare retto si hanno, rispettivamente, le seguenti formule per le aree delle loro superfici laterali:

avendo indicato con p il semiperimetro della base della piramide, con r il raggio di base del cono e con a, in entrambi i casi, l’apotema.