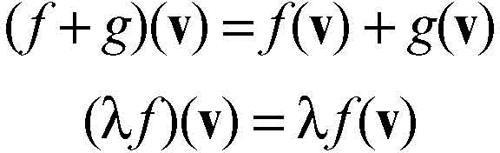applicazione lineare

applicazione lineare

applicazione lineare detta anche omomorfismo di spazi vettoriali, è una applicazione ƒ: V → W tra due spazi vettoriali V e W su un campo K, con le due seguenti proprietà:

• ƒ(v₁ + v₂) = ƒ(v₁) + ƒ(v₂), per ogni coppia di vettori v₁, v₂ appartenenti a V;

• ƒ(λv) = λƒ(v), per ogni scalare λ appartenente a K e per ogni vettore v appartenente a V.

Le due proprietà possono essere riscritte in modo equivalente attraverso un’unica uguaglianza come segue: per ogni coppia di elementi λ, μ appartenenti a K e per ogni coppia di vettori v₁, v₂ appartenenti a V risulta ƒ(λv₁ + μv₂) = λƒ(v₁) + μƒ(v₂). L’insieme delle applicazioni lineari da V in W è indicato con il simbolo Hom_K(V, W) e ha anch’esso una naturale struttura di spazio vettoriale su K rispetto alle operazioni di addizione e moltiplicazione per uno scalare definite come segue:

Nel caso in cui il codominio W coincide con il dominio V, si parla allora di endomorfismo di V; lo spazio degli endomorfismi di V si indica più in particolare con il simbolo End(V). Un omomorfismo invertibile (cioè un omomorfismo che sia una biiezione) si dice isomorfismo di spazi vettoriali; un isomorfismo di uno spazio vettoriale V in sé stesso è detto un automorfismo di V. Lo spazio degli automorfismi di V si indica con il simbolo Aut(V) e ha anch’esso una naturale struttura di spazio vettoriale. Sia ƒ: V → W un’applicazione lineare; si definisce allora il nucleo di ƒ (indicato con il simbolo Ker(ƒ)) come l’insieme dei vettori v appartenenti a V la cui immagine è il vettore nullo di W; formalmente Ker(ƒ) = {v ∈ V: ƒ(v) = 0}. Il nucleo di ƒ, come l’immagine di ƒ (indicata con il simbolo Im(ƒ)), sono sottospazi vettoriali rispettivamente del dominio e del codominio dell’applicazione e sono legati dall’isomorfismo V/Ker(ƒ) ≅ Im(ƒ) (primo teorema di omomorfismo; → omomorfismo e isomorfismo, teoremi di).

Se sia V che W hanno dimensione finita, allora resta definito un isomorfismo tra lo spazio Hom_K(V, W) degli omomorfismi da V in W e lo spazio M_m×n(K) delle matrici m × n a coefficienti nel campo K. Indicando con dim la dimensione di uno spazio vettoriale e supponendo dim(V) = n e dim(W) = m, si fissano due basi {v₁, ..., v_n} e {w₁, ..., w_m} rispettivamente nello spazio di partenza e nello spazio di arrivo. Allora, sostituendo ogni vettore v appartenente a V con il vettore n-dimensionale dei suoi coefficienti nella base fissata di V e ogni vettore w appartenente a W con il vettore m-dimensionale dei suoi coefficienti nella base fissata di W, e indicando con [w]_i la componente di un vettore w appartenente a W secondo l’i-esimo elemento della base fissata di W (cioè il suo i-esimo coefficiente, una volta scritto come combinazione lineare degli elementi della base fissata), si può descrivere completamente l’applicazione lineare ƒ nei termini della sua azione sui coefficienti dei vettori di V. Sia A(ƒ) la matrice m × n a coefficienti in K la cui entrata a_ij di posto i, j è definita da a_ij = [ƒ(v_j)]_i; allora l’applicazione Ψ: Hom_K(V, W) → M_m×n(K) definita da Ψ(ƒ) = A(ƒ) è un isomorfismo di spazi vettoriali. È bene osservare che l’isomorfismo appena descritto dipende in modo determinante dall’aver fissato le due basi in V e W: cambiando basi si otterrà un diverso isomorfismo tra Hom_K(V, W) e M_m×n(K), vale a dire una diversa rappresentazione dell’applicazione lineare ƒ in termini di matrici. Se ci si limita a considerare endomorfismi di uno spazio vettoriale V, allora questi saranno descritti da matrici quadrate di dimensione dim(V). In questo caso è allora possibile mostrare che tutte le matrici della forma A(ƒ), ottenibili nel modo descritto da uno stesso endomorfismo ƒ di V a partire da due basi rispettivamente di V e W, saranno tra di loro coniugate tramite una matrice invertibile (→ coniugio), e, viceversa, ogni coppia di matrici coniugate definisce uno stesso endomorfismo di V, che pertanto coincide con una classe di coniugio di matrici quadrate di dimensione dim(V).