applicazione
applicazione
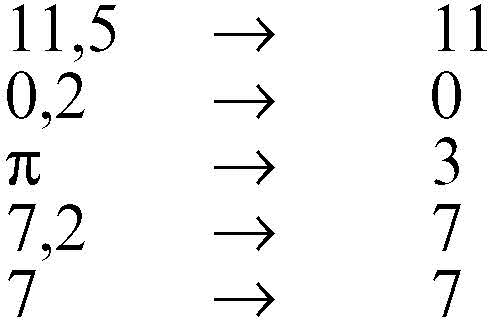
applicazione particolare corrispondenza ƒ tra due insiemi X e Y che associa a ogni elemento x di X uno (e un solo) elemento di Y, che viene indicato con il simbolo ƒ(x). Una tale corrispondenza si dice un’applicazione di X in Y e si scrive ƒ: X → Y, mentre gli insiemi X e Y sono detti rispettivamente dominio e codominio di ƒ. L’applicazione è detta anche mappa o → funzione. Per esempio, la legge «si consideri la parte intera di un numero reale positivo x» è un’applicazione che opera in questo modo:
Il dominio è l’insieme dei numeri reali positivi mentre il codominio è l’insieme dei numeri interi positivi. Alcuni autori non richiedono la condizione che a ogni elemento del dominio X sia associato un elemento di Y e quindi distinguono tra il dominio e il suo sottoinsieme formato dagli elementi ai quali effettivamente sono associati elementi di Y: questo sottoinsieme è allora detto insieme di definizione (o anche, con terminologia antiquata, campo di esistenza, anche se non si tratta di un campo in senso algebrico).
Se x è un elemento di X, l’elemento ƒ(x) di Y è detto valore di ƒ in x o immagine di x tramite ƒ; viceversa, se y appartiene a Y, l’insieme degli elementi di X la cui immagine tramite ƒ è y è detto antimmagine (o anche preimmagine o controimmagine) di y ed è indicato con il simbolo ƒ −1(y). Il sottoinsieme costituito dagli elementi ƒ(x) al variare di x in X è detto immagine di ƒ. L’applicazione ƒ è detta suriettiva (o anche surgettiva o suriezione) se la sua immagine coincide con Y; è invece detta iniettiva (o anche iniezione) se la preimmagine di ogni elemento della sua immagine è costituita da un solo elemento, cioè se vale la seguente implicazione: se x1 e x2 sono due elementi di X tali che ƒ(x1) = ƒ(x2) allora risulta x1 = x2. Infine, un’applicazione che è contemporaneamente iniettiva e suriettiva è detta biiettiva (o anche corrispondenza biunivoca o biiezione). Se un’applicazione è biiettiva, ha allora senso considerare la sua inversa, indicata con il simbolo ƒ −1 (da non confondere con l’analogo simbolo che indica la preimmagine di un insieme), definita come l’applicazione ƒ −1: Y → X che associa a ogni elemento y di Y l’unico elemento x di X per cui si ha ƒ(x) = y. In modo equivalente, l’inversa di ƒ è definita come l’unica applicazione g: Y → X tale che g(ƒ(x)) = x e f(g(y)) = y, dove x appartiene a X e y appartiene a Y. Più in generale, a patto di restringere il codominio Y all’immagine di ƒ (a patto cioè di “suriettivizzare” l’applicazione), ha senso considerare l’applicazione inversa di ƒ, purché quest’ultima sia iniettiva. Un’applicazione iniettiva ƒ:X → X si dice involutoria (o involuzione) se vale f(ƒ(x)) = x cioè se, una volta suriettivizzata, essa coincide con la sua inversa.
L’esempio precedente (l’applicazione «parte intera» ristretta ai numeri positivi) mostra un’applicazione suriettiva, perché effettivamente ogni numero intero positivo è immagine (cioè corrispondente) di qualche numero reale positivo, ma non iniettiva, perché a infiniti numeri reali positivi corrisponde lo stesso numero intero positivo (per esempio, a tutti i numeri reali x tali che 3 ≤ x < 4 corrisponde 3). Non è dunque una biiezione. Esempi di applicazione involutoria sono invece forniti dalla legge «cambia segno» nell’insieme dei numeri reali (ƒ(x) = −x), che applicata due volte dà l’identità, e dalla simmetria assiale nel piano.