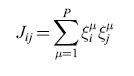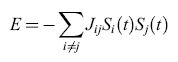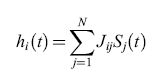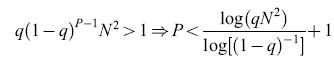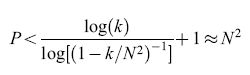Apprendimento dinamico della memoria di lavoro: una realizzazione elettronica
Apprendimento dinamico della memoria di lavoro: una realizzazione elettronica
In questo saggio presenteremo una realizzazione in elettronica analogica e asincrona di una rete neurale, ispirata da un lato alla neurofìsiologia, dall'altro ai modelli teorici della dinamica neuronale e sinaptica nella corteccia associativa. Passeremo in rassegna alcuni risultati sperimentali che evidenziano un ruolo centrale della retroazione nel modulo corticale coinvolto nella memoria di lavoro, e illustreremo i vincoli teorici per l'apprendimento. I risultati sperimentali suggeriscono che i modelli teorici ad attrattori possono fornire un naturale substrato per la formazione della memoria di lavoro. Attraverso una serie di esempi, mostreremo come il dispositivo illustrato abbia la capacità di sviluppare la memoria di lavoro da un flusso di stimoli in ingresso. Nuovi dispositivi, ancora in corso di sviluppo, potranno fornire in futuro uno strumento euristico per l'analisi delle teorie sulla dinamica dell'apprendimento.
La memoria di lavoro e la classificazione degli stimoli
La classificazione degli stimoli ambientali viene considerata da tempo uno dei misteri fondamentali del sistema cognitivo (Edelman, 1987). Il cervello è in grado di elaborare stimoli ambientali che si presentano in gran numero, e possono cambiare rapidamente. Questi stimoli, inoltre, si succedono nel tempo in sequenze impredicibili e lo stesso stimolo visivo, per esempio, quando appare più volte, non si presenta alla retina nello stesso modo. Malgrado tale variabilità il cervello riesce ugualmente a operare delle classificazioni che consentono, da un lato, di raggruppare stimoli simili tra loro e, dall'altro, di discriminare in modo efficace stimoli differenti. Le classificazioni vengono apprese e utilizzate a diversi livelli: al livello più semplice sono raggruppati stimoli che si presentano con caratteristiche simili agli apparati sensoriali, mentre una gerarchia di classificazioni via via più complesse corrisponde, per esempio, alla dipendenza dal contesto o alle relazioni con il linguaggio. In questo saggio sarà affrontato il problema della classificazione al livello più semplice, e l'analisi sarà focalizzata sulle classificazioni che non hanno origine genetica, ma sono apprese dall'esperienza.
La sperimentazione in neurofisiologia
La memoria attiva e la classificazione: osservazioni sperimentali
Un modo per mettere in relazione il fenomeno (psicologico o psicofisico) della classificazione con il substrato cerebrale consiste nello studiare la neurofisiologia di animali superiori durante lo svolgimento di compiti che comportino classificazione. Nel corso di una lunga tradizione sperimentale, iniziata con il lavoro pionieristico di IM. Fuster (1973) e H. Niki (1974) nei primi anni Settanta, si è giunti al seguente paradigma sperimentale. Delle scimmie vengono addestrate a seguire una lunga sequenza di prove sperimentali (trial): la scimmia fissa uno schermo, su cui una figura astratta scelta come campione si presenta per breve tempo, e, dopo un ritardo relativamente lungo, la deve paragonare con un' altra figura astratta di confronto scelta a caso (uguale alla figura campione nel 50% dei casi). In una versione recente di questo tipo di esperimenti, detti di confronto ritardato con un campione (DMS, Delayed Match to Sample), Y. Miyashita e collaboratori (1988) sono riusciti ad addestrare delle scimmie ottenendo buone prestazioni su un centinaio di stimoli campione. Queste figure sono di due tipi: frattali e descrittori di Fourier. Entrambi i tipi vengono generati da algoritmi che contengono elementi casuali; la natura astratta e casuale di queste immagini assicura che esse non appartengano al patrimonio di esperienza passata, o a quello ereditario, della scimmia. L'elaborazione di queste immagini da parte del sistema biologico è, molto probabilmente, il risultato di un apprendimento a partire dall' esperienza.
Dopo una fase di addestramento relativamente lunga, in cui ogni stimolo viene presentato molte volte, sia come campione che come stimolo di confronto, si osserva un insieme di distribuzioni di attività neuronale nella parte anteriore della corteccia inferotemporale della scimmia durante il periodo di ritardo tra la presentazione della figura campione e quella di confronto. In tale intervallo di tempo si osserva, in assenza di stimolazione, che alcune delle cellule mantengono frequenze di emissione di impulsi significativamente più alte rispetto a quelle precedenti lo stimolo campione. L'insieme di cellule che presentano tale attivazione è diverso per ogni stimolo campione. Pertanto, la distribuzione dell'attività delle cellule nel periodo di ritardo (DAD, Delay Activity Distribution) costituisce una rappresentazione interna dello stimolo campione, e preserva l'informazione che lo riguarda per alcuni secondi dopo la sua scomparsa, fino all'arrivo dello stimolo di confronto. Inoltre, per tutte le 100 immagini mostrate, le diverse distribuzioni di attività si manifestano in un'area ristretta (1 mm²) della corteccia inferotemporale.
In che senso le distribuzioni di attività osservate nel periodo di ritardo possono essere considerate come delle classificazioni? In primo luogo, il numero di tali distribuzioni, che si formano durante l'addestramento, è una piccola frazione del numero totale di stimoli visivi cui la scimmia è stata sottoposta durante quel periodo. Sia durante le sessioni di lavoro, che costituiscono una parte relativamente piccola del periodo di veglia della scimmia, sia nel resto del tempo, la scimmia riceve un numero enorme di stimoli. Inoltre ogni stimolo, quando viene presentato sullo schermo, provoca risposte visive alquanto diverse nella corteccia della scimmia, a causa di piccoli movimenti oculari, o del rumore presente lungo il percorso visivo dalla retina alla corteccia inferotemporale.
Le variazioni si possono osservare nelle diverse risposte delle cellule alla stessa immagine. Ciò nonostante, per ogni insieme di stimoli simili (cioè per ogni classe corrispondente a una data immagine) viene trasmessa un'unica distribuzione di attività durante il periodo di ritardo che segue la scomparsa dello stimolo. D'altra parte, sovrapponendo del rumore alle immagini stesse (Amit et al., 1997), si osserva che tutto un insieme di stimoli visivi, simili a una delle immagini generate, provoca la stessa distribuzione di attività nel periodo di ritardo. Infine, immagini che non siano state usate nel corso dell' addestramento non sembrano provocare alcuna attività selettiva nel periodo di ritardo, almeno in questa regione della corteccia. Il quadro che emerge da questi esperimenti è il seguente. Esiste un piccolo modulo (più o meno di l mm², con circa 10⁵ cellule) nella corteccia inferotemporale anteriore che, dopo aver ricevuto una sequenza molto lunga di stimoli (ogni immagine viene presentata centinaia di volte), riesce a estrarre la presenza di insiemi di stimoli tra di loro simili, nel contesto di un compito dato, e a generare una sola rappresentazione per ognuno di questi insiemi, cioè la corrispondente distribuzione di frequenze di emissione durante il periodo di ritardo. Questa distribuzione di frequenze, o DAD, costituisce una rappresentazione interna della classe di stimoli.
Ruolo psicologico delle DAD
Gli esperimenti di confronto ritardato con un campione che abbiamo descritto suggeriscono che le DAD possano rappresentare un meccanismo utile e necessario per trasmettere l'informazione relativa a uno stimolo, ai fini di una elaborazione che deve avvenire parecchio tempo dopo la scomparsa dello stimolo stesso. Nel momento in cui appare sullo schermo la seconda immagine, la prima è scomparsa da tempo, ma l'informazione a essa relativa è essenziale per il confronto con la seconda immagine, e quindi per lo svolgimento del compito. Esperienze cognitive di questo tipo sono molto comuni: per esempio, se si va a incontrare all'aeroporto qualcuno che si conosce e di cui ci è stato detto il nome, anche se l'incontro ha luogo dopo un tempo relativamente lungo dal momento in cui si è ascoltato il nome stesso, l'informazione relativa all'aspetto della persona viene mantenuta attiva, e risulta disponibile al momento giusto. Questa situazione è simile a quella osservata negli esperimenti compiuti da P. Goldman-Rakic e collaboratori (1987), in cui delle scimmie vengono addestrate a spostare gli occhi verso la direzione indicata da uno stimolo visivo, che funge da indizio, alcuni secondi dopo la scomparsa dell'indizio stesso. Anche in questi esperimenti si trova che cellule appartenenti a una porzione molto localizzata della corteccia mostrano, nel periodo di ritardo, un'attività selettiva rispetto alla direzione.
Come si collocano queste DAD nella discussione sui tipi di memoria a breve, lungo o medio termine? il tipo di memoria relativa all'attività nel periodo di ritardo dovrebbe essere comune a tutte e tre le categorie. L'informazione trasmessa dopo il periodo di ritardo non viene appresa durante lo svolgimento del compito, ma nella lunga esperienza che lo precede. Le immagini sono dunque familiari; una di esse deve essere posta in uno stato attivo dal primo stimolo, così da consentire delle operazioni su tale stimolo nel periodo successivo alla sua scomparsa. Pertanto, si suggerisce di riferire le espressioni "breve termine" e "lungo termine" al periodo della vita dell'animale in cui una particolare immagine rimane familiare, cioè al periodo in cui quella immagine può ancora generare una specifica distribuzione di attività nel periodo di ritardo.
DAD e paradigma hebbiano
Secondo la terminologia introdotta da D. Hebb, la memoria (il processo di familiarizzazione) è caratterizzata dal fatto che, durante l'addestramento, si manifesta un particolare cambiamento nelle sinapsi, detto engramma (Hebb, 1949). l cambiamenti sinaptici indotti dall'apprendimento producono il substrato per la propagazione dell' attività nel periodo di ritardo da parte dell' insieme locale di neuroni (l'attività riverberante, nella terminologia di Hebb). La sede della memoria è dunque la sinapsi, e l'intervallo di tempo in cui vengono preservati i cambiamenti sinaptici stabilisce la persistenza della memoria. L'attività riverberante nel periodo di ritardo corrisponde in questa interpretazione al fatto che uno stimolo familiare, una volta appreso, pone la memoria corrispondente, codificata nella struttura sinaptica, in uno stato attivo, in grado di mantenere disponibile nel tempo in modo autonomo l'informazione sullo stimolo stesso.
L'apprendimento ha luogo durante la presentazione di un'immagine (lo stimolo) che aumenta, in modo selettivo, la frequenza di emissione di un sottoinsieme di neuroni. Le sinapsi che connettono due neuroni con risposte forti allo stimolo, cioè con elevate frequenze di emissione, si potenziano, diventando più efficaci, mentre quelle che connettono coppie di cellule con attività anticorrelate si indeboliscono (depressione sinaptica). Questi due effetti sono denominati rispettivamente potenziamento a lungo termine (L TP, Long Term Potentiation) e depressione a lungo termine (L TD, Long Term Depression). Ci si attende dunque che una simile dinamica della matrice sinaptica possa generare, in risposta agli stimoli in ingresso, una struttura sinaptica particolare. Tale struttura deve essere in grado di sostenere una distribuzione di attività simile a quella indotta dallo stimolo, anche dopo la sua scomparsa. Inoltre, essa deve avere la possibilità di sostenere in modo autonomo un'ampia varietà di attività riverberanti, come nell' esperimento descritto sopra.
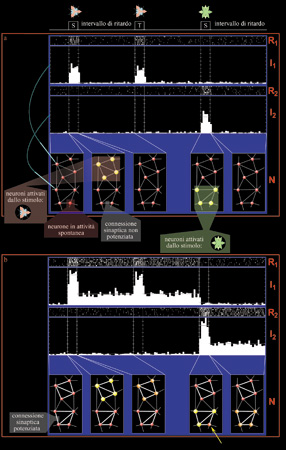
La figura (fig. 2) illustra, con una simulazione, lo sviluppo di questo schema, in cui diverse immagini, che provocano una risposta visiva in un gruppo di cellule, creano delle DAD attraverso un processo simile a quello ipotizzato da D. Hebb (1949). La riga in alto mostra il protocollo temporale di due prove consecutive: il primo stimolo campione (simbolo S) è seguito da un periodo di assenza di stimoli, e quindi dalla presentazione dello stimolo di confronto (T), che conclude la prima prova; dopo un ulteriore periodo di assenza di stimoli, viene presentato lo stimolo campione della seconda prova (secondo simbolo S). La sequenza delle prove viene ripetuta più volte per garantire una descrizione statisticamente significativa dell' attività dei neuroni. Nella figura 2 è anche mostrata una tipica registrazione simulata di due neuroni durante il protocollo sopra descritto. Per ogni neurone sono riportati i cosiddetti raster (R1 e R2), nei quali ogni sequenza orizzontale di tracce bianche rappresenta la successione temporale di impulsi emessi dal neurone in una ripetizione della prova, e gli istogrammi (I1 e 12), derivati dai raster, dell'attività media del neurone nelle ripetizioni delle prove con lo stesso stimolo campione. Tali istogrammi, costruiti a partire dall' attività relativa a ogni stimolo, vengono per questo chiamati PeriSTimulus Histograms (PSTH). La figura 2 mostra, infine, una porzione di 8 neuroni della rete cui appartengono i due neuroni registrati, nelle varie fasi delle prove. Ogni neurone è rappresentato da una sferetta, tanto più grande e luminosa quanto più il neurone è attivo. Lo spessore delle barre che uniscono i due neuroni è proporzionale all'efficacia della sinapsi che li connette.
Prima dell'apprendimento la rete, in assenza di stimoli, è sempre in attività spontanea (i neuroni emettono impulsi a frequenze basse); durante la presentazione dello stimolo, i neuroni della rete che rispondono agli stimoli visivi aumentano di molto la loro frequenza di emissione e, in base a un meccanismo hebbiano di LTP, le connessioni sinaptiche tendono a potenziarsi tra di loro. Dopo molte ripetizioni della prova le sottopopolazioni attivate da stimoli diversi hanno sinapsi potenziate alloro interno (v. figura 2). Tale potenziamento selettivo è in grado di sostenere collettivamente lo schema di attività (l'attrattore) provocato da ogni stimolo, anche dopo la scomparsa dello stimolo stesso: i neuroni eccitati dallo stimolo rimangono attivi dopo la sua rimozione, ed eccitandosi l'un l'altro emettono a frequenze nettamente maggiori di quelle spontanee, a causa dell'intensa retroazione. Nell'esempio mostrato, alla presentazione del secondo stimolo campione l'insieme dei neuroni attivati dallo stimolo non coincide completamente con quello dei neuroni attivi durante la fase di apprendimento: il neurone indicato dalla freccia gialla non è attivato dallo stimolo e ha attività di ritardo. Ciò avviene quando si presenta alla rete una versione leggermente modificata dello stimolo. Dall'attività che segue la rimozione dello stimolo si vede che la struttura sinaptica permette la ricostruzione dinamica dello schema di attività appreso. Il quadro fin qui esposto, pur non essendo completo, descrive in modo soddisfacente i processi dell'apprendimento e della memoria, e fornisce un'interpretazione promettente dei risultati di Miyashita e Goldman-Rakic. Se l'interpretazione di questi esperimenti è corretta, lo schema hebbiano potrebbe esserne il meccanismo di base. Rimane da verificare l'ipotesi che tale schema sia sufficiente per produrre un classificatore con apprendimento. Gli aspetti teorici dei modelli neuronali Il modello di Hopfield Dal punto di vista dei modelli neuronali, vi sono tre aspetti da analizzare. Prima di tutto, bisogna capire se esiste una matrice sinaptica in grado di sostenere molte distribuzioni persistenti di attività selettiva, ognuna con un suo bacino di attrazione che defmisce una classe di stimoli. In secondo luogo, è necessario chiedersi se una semplice dinamica hebbiana possa portare a una struttura sinaptica di questo tipo. Infine, occorre analizzare, da un punto di vista teorico, i vincoli imposti da una realizzazione materiale, sia essa biologica o elettronica.
Alla prima domanda viene data una risposta dal modello di Hopfield (Hopfield, 1982; Amit, 1989). La comprensione del modello è facilitata dalla seguente metafora: la dinamica della rete è analoga alla caduta di un grave in un paesaggio con valli e alture. Ogni punto del paesaggio corrisponde a una configurazione di stati di attività della rete, e la tendenza ad andare verso il basso è una conseguenza della dinamica neuronale. Ogni fondovalle corrisponde a uno stato di equilibrio (attrattore), verso il quale tendono tutti gli stimoli (cioè le condizioni iniziali della rete) che sono nel suo bacino di attrazione, ovvero che appartengono alla stessa classe. Lo stato a fondovalle è rappresentativo dell'intera classe di stimoli e costituisce una rappresentazione interna della classe. La struttura sinaptica determina l'altitudine del paesaggio in ogni punto (energia del sistema), e dunque contiene l'informazione sulla localizzazione dei fondivalle e sulla grandezza dei bacini di attrazione. A sua volta la struttura sinaptica viene costruita come risultato dell'apprendimento, e dunque dipende dalla struttura degli stimoli presentati.
Il modello di Hopfield fornisce un esempio di struttura sinaptica che genera un paesaggio con le proprietà appena descritte. Ciascun neurone può trovarsi in due soli stati (+1, -1), corrispondenti ad alta e bassa frequenza di emissione. Una rete di N neuroni di questo tipo può avere 2N stati differenti, e lo spazio sul quale il paesaggio viene disegnato si estende a tutti questi stati. Ogni stato della rete è una 'parola' a N bit, che indicheremo con {ξiμ}, dove i=l,..,N è l'indice del neurone della rete, e μ indica lo stimolo preso in considerazione. Per μ fissato, questa parola a N bit corrisponde a uno stato di tutti i neuroni nella rete quando viene presentato lo stimolo contraddistinto da μ. Una matrice sinaptica che garantisce che un insieme particolare di stati neuronali, {ξiμ}, sia uno stato di equilibrio (un attrattore) della dinamica neuronale, è data da:
formula [
l]
dove Jij è l'efficacia della sinapsi che modula il segnale emesso dal neurone presinaptico j per depolarizzare il neurone postsinaptico i. P è il numero di stimoli che sono stati impressi nella rete come stati persistenti, corrispondenti ai minimi (fondivalle) del paesaggio. L'energia del sistema (l'altitudine nel paesaggio) è data dall'espressione:
formula [2]
dove Si(t) e Sj(t) rappresentano lo stato dei neuroni i e j al tempo t. La dinamica della rete viene concepita nel modo seguente: dato una stato di tutti neuroni al tempo t, {Si(t)}, ogni neurone calcola il proprio input sinaptico, cioè la sua depolarizzazione:
formula [3]
e, assumendo una soglia uguale a 0, il nuovo stato del neurone i vale:
Si(t+δt)=l se hi>0, [4]
Si(t+δt)=-l se hi<0.
A ogni passo di questa dinamica l'energia E diminuisce, cioè il punto rappresentativo dello stato della rete nel paesaggio scende verso un fondovalle.
Questo sistema dinamico presenta la maggior parte delle caratteristiche richieste. Quando P non è troppo elevato, le p distribuzioni di attività {ξiμ} sono proprio corrispondenti ai fondi valle del paesaggio di energia.
Il modello di Hopfield non è molto realistico dal punto di vista neurobiologico, e sono stati costruiti dei modelli più elaborati per analizzare i fenomeni di memoria attiva e passiva. Tuttavia, esso presenta molte delle caratteristiche dei modelli più realisti ci. È pertanto utile per discutere le promesse e le limitazioni dei sistemi di classificazione neuronale.
La prima domanda da porsi è se questo modello sia in grado di imparare a classificare. Supponiamo che i P stimoli ξiμ siano presentati alla rete uno dopo l'altro, e che ogni stimolo imponga ai neuroni lo stato prescritto dalla sua struttura. Supponiamo anche che le Jij cambino semplicemente aggiungendo all'efficacia sinaptica il prodotto ξiμξiμ degli stati imposti dallo stimolo ai due neuroni che sono connessi dalla sinapsi. Questo schema di funzionamento non è molto diverso da un meccanismo hebbiano. Se non interviene nessuna ulteriore modifica, il sistema risultante è un classificatore che ha imparato a classificare dalla propria esperienza. Ognuno degli stati appresi attrae un grosso numero di stimoli futuri (il suo bacino di attrazione) verso la stessa distribuzione di attività persistente.
In termini di paesaggio possiamo pensare a una condizione iniziale della rete con sinapsi casuali, che corrisponde in generale a una successione molto irregolare di alture e di valli (fig. 3); la posizione del fondo delle valli sarà essenzialmente scorrelata dagli stimoli. Per effetto delle modificazioni sinaptiche il paesaggio si modifica gradualmente, e valli sempre più ampie e profonde si scavano in corrispondenza delle configurazioni che codificano gli stimoli. Alla fine, se la rete è sotto il limite di capacità di memoria, queste valli dominano il paesaggio (pur essendovi la possibilità di valli minori, o di piccole valli entro quelle maggiori).
Un tale sistema funziona sorprendentemente bene, anche quando viene esposto a un flusso 'rumoroso' di stimoli, in cui alcuni stimoli appartengono a classi, mentre altri sono scorrelati tra di loro e con le classi. Anche se il numero di stimoli transitori presentati alla rete è molto più grande del numero di quelli appartenenti alle classi, queste manterranno un ampio bacino di attrazione. Anche se ognuno degli stimoli transitori cambia la matrice sinaptica come gli altri stimoli, i cambiamenti prodotti tendono a cancellarsi statisticamente e non disturbano il richiamo delle classi. Per ognuno degli stimoli transitori viene formato un attrattore, ma appaiono molti membri di ogni classe, e la rete è in grado di estrarre un prototipo rappresentativo di ognuna di esse, il cui bacino di attrazione sarà più profondo e più esteso.
In effetti qualsiasi rumore presente nella rete tende a destabilizzare le piccole valli che corrispondono agli attrattori minori. Genericamente si può associare un 'rumore' a qualunque causa di stocasticità che si sovrapponga alla dinamica deterministica del neurone, descritta dall' equazione [4]. Questo rumore provoca occasionalmente un movimento 'contro la gravità' del punto rappresentativo della rete nel paesaggio, in cui si risale brevemente il pendio invece di scendere verso il fondo valle. Se la sorgente di rumore non è troppo forte, il suo effetto non cambia la capacità, da parte delle valli ampie e profonde, di attrarre verso il basso gli stati della rete che si trovano sul pendio. Tale effetto, però, può essere sufficiente a offrire una via di fuga agli stati che, altrimenti, resterebbero intrappolati nelle piccole valli create da stimoli occasionali.
Difficoltà di apprendimento in dispositivi reali
La difficoltà maggiore che si incontra nel realizzare, per esempio in elettronica, un sistema come quello appena descritto sta nella profondità analogica richiesta per le sinapsi: la regola per cambiare l'efficacia sinaptica prevede che il dispositivo che realizza la sinapsi sia in grado di memorizzare un numero di valori differenti pari almeno al massimo numero di classi che devono essere apprese, e questo numero può essere molto elevato. Il dispositivo sinaptico, che nei sistemi biologici è molto piccolo rispetto al neurone, deve essere in grado di preservare il valore dell'efficacia sinaptica in modo stabile su scale di tempo dell' ordine di giorni, se non di anni. Tuttavia, allo stesso tempo, deve essere in grado di adattarsi e di imparare in tempi molto brevi, dell'ordine di secondi.
Questi sono vincoli molto stringenti, e un dispositivo che soddisfi tutte queste richieste non è disponibile, allo stato attuale. Sembra piuttosto improbabile che il meccanismo di apprendimento presente nei sistemi biologici si basi su un dispositivo così difficile da realizzare.
Il nostro gruppo si è proposto di realizzare una serie di dispositivi sinaptici di capacità più limitate rispetto a quelle elencate in precedenza ma, d'altra parte, facilmente realizzabili e, ciò che è più importante, tali da non sacrificare nessuna delle capacità di elaborazione relative all'apprendimento e all'espressione di DAD come memoria attiva.
È interessante notare come la costruzione della memoria di un computer consista nell'organizzare semplici elementi a due stati, i bit, ognuno dei quali può mantenere il suo stato per tempi lunghi (a spese dell'energia fornita dall'esterno). L'immagazzinamento di grandezze con buona profondità analogica viene ottenuto organizzando la memoria in 'parole' di B bit, in grado di assumere (e mantenere) 2B diverse configurazioni. Occorre poi una 'intelligenza' (il processore) che assegni un valore a ognuno dei bit in base alla sua posizione. A patto di definire e gestire un'opportuna organizzazione di elementi di memoria binari stabili, si può costruire una memoria 'universale'. Una logica a più valori ridurrebbe il numero di elementi necessari a parità di informazione, ma complicherebbe molto la struttura dei singoli elementi stabili.
Queste osservazioni generali suggeriscono, anche nel nostro contesto, di semplificare al massimo l'elemento base della memoria, cioè la sinapsi. La riduzione drastica della profondità analogica della sinapsi, che può risolvere il problema del mantenimento a lungo termine, solleva però altre due questioni. La prima riguarda la funzionalità: è possibile che una rete di sinapsi binarie sia in grado di sostenere la varietà di DAD che sono espressione del processo di classificazione? La seconda riguarda l'apprendimento: esiste una dinamica dell' efficacia sinaptica che sia realizzabile, e che porti a una matrice sinaptica con le caratteristiche desiderate?
La prima questione ha avuto una interessante risposta quando H. Sompolinsky (1986) chiarì che una rete di Hopfield perde poco, dal punto di vista delle capacità di elaborazione, anche se si riducono a due i valori di ogni sinapsi (si mantiene solo il segno algebrico della sommatoria nell'equazione [l]). Se però, da un lato, si ha una risposta positiva al problema della funzionalità, dall'altro sorgono nuove difficoltà legate alla questione dell'apprendimento. Nel contesto che abbiamo descritto la matrice sinaptica di una rete di Hopfield deve prima essere ottimizzata, e solo alla fine essere ridotta a una matrice di valori binari.
Da un lato non è chiaro come l'apprendimento possa proseguire, dopo questa riduzione, al presentarsi di nuovi stimoli. Dall'altro, se la riduzione esprime il fatto che il dispositivo sinaptico può mantenere una buona profondità analogica solo per piccoli intervalli di tempo Δt, e possiede un piccolo numero di stati stabili, si pone il problema di scegliere a quale stadio della formazione della matrice sinaptica debba essere effettuata la riduzione. Questa riduzione deve essere effettuata entro un tempo minore di Δt, altrimenti nuovi stimoli possono ribaltare il segno finale portando a una matrice che non ha più le caratteristiche desiderate. Se la riduzione interviene su questa scala, bisogna assicurarsi che tutti gli stimoli da memorizzare vengano presentati alla rete in una finestra temporale relativamente breve.
Un'alternativa semplice consiste nell'assumere che la sinapsi sia un dispositivo analogico solo su scale di tempo brevi, e che su scale di tempo lunghe intervenga un meccanismo di ripristino, che preserva solo uno dei valori di un insieme discreto. Tutti gli altri valori sono instabili e, in assenza di stimoli, sono attratti verso uno dei valori di questo insieme, che vengono mantenuti indefinitamente. Tra un valore stabile e l'altro vi è una soglia, che discrimina i valori analogici attratti verso un valore da quelli attratti verso l'altro.
Quando si presenta uno stimolo, viene attivata una sorgente che dipende dall' attività dei due neuroni connessi dalla sinapsi, e che tende a portare l'efficacia sinaptica verso uno degli altri valori stabili. Se, al momento della rimozione dello stimolo, l'efficacia ha attraversato una delle soglie, la sinapsi verrà attratta verso uno dei valori stabili, e sarà avvenuta una transizione. Altrimenti il valore dell'efficacia verrà nuovamente attratto verso il valore stabile iniziale, e lo stimolo non avrà indotto alcun cambiamento. Un tale schema di dinamica di apprendimento risulta il più naturale per la realizzazione di un dispositivo sinaptico reale, sia esso elettronico o biologico. Prima di intraprendere la descrizione dell'hardware realizzato sulla base di questo schema, dobbiamo premettere alcune considerazioni sulle implicazioni a livello funzionale.
I vincoli di un apprendimento realistico
La dinamica di apprendimento appena descritta può essere schematizzata come una serie di transizioni da uno stato stabile all'altro: durante la presentazione di ogni stimolo la sinapsi viene spinta verso l'alto (potenziamento) o verso il basso (depressione), e alla fine può accadere che abbia lasciato lo stato precedente per ritrovarsi in un altro stato stabile. Questo nuovo stato stabile viene preservato fino alla presentazione di un nuovo stimolo.
In questo scenario la situazione è assai diversa da quella descritta in precedenza: l'informazione sugli stimoli presentati nel passato si dissolve con estrema rapidità, in quanto ogni nuovo cambiamento della matrice sinaptica tende a cancellare la traccia del passaggio degli stimoli precedenti. Per capire come ciò possa accadere consideriamo il caso estremo di una rete con sinapsi binarie. Nel momento in cui si presenta un nuovo stimolo, la sinapsi cerca di assecondare le spinte della sorgente hebbiana, in modo da acquisire l'informazione sulla struttura dello stimolo presentato. Se l'apprendimento è deterministico, per ognuna delle sinapsi lo stato successivo alla presentazione dello stimolo sarà scelto univocamente tra i due soli possibili, sulla base della sorgente hebbiana da essa vista, indipendentemente dal suo stato di partenza e, quindi, dalla sua storia passata. In questo senso, la struttura sinaptica perde memoria degli stimoli passati a ogni presentazione di un nuovo stimolo. La sola 'memoria' residua dipende, in questo caso, dalle accidentali somiglianze tra gli stimoli che si succedono, che possono rendere implicitamente richiamabili gli stimoli tra di loro sufficientemente simili, indipendentemente dalla loro posizione nella sequenza temporale. La fenomenologia descritta, giustificata in termini quantitativi nei lavori di D.J. Amit e collaboratori (1994; 1997), non muta qualitativamente aumentando il numero di stati stabili delle sinapsi, purché tale numero resti finito.
Il metodo dell'apprendimento stocastico
L'esempio presentato suggerisce che si possa modificare solo una parte delle sinapsi pur continuando ad acquisire abbastanza informazione da poter richiamare, successivamente, lo stimolo presentato, preservando così in memoria almeno la traccia di un numero più elevato di stimoli; ciò non vuoI dire che questa traccia sia sufficiente a richiamarli. Una dinamica plausibile dell'efficacia sinaptica, che non usa esplicitamente informazioni globali sul flusso degli stimoli, prevede i passi seguenti. Per ogni sinapsi viene deciso se essa debba essere potenziata o depressa, sulla base dell'attività dei due neuroni che essa connette. Una transizione permessa viene quindi effettuata con probabilità q. A parità di condizioni sull'attività dei neuroni presinaptico e postsinaptico, talvolta si hanno le transizioni previste, e talvolta l'efficacia sinaptica rimane inalterata. Se lo stato della sinapsi è già potenziato e si è deciso di effettuare un ulteriore potenziamento, allora la sinapsi rimane inalterata, perché non si può andare oltre al livello massimo. La situazione è analoga se si parte da uno stato depresso ed è stata decisa una ulteriore depressione.
Con questo tipo di apprendimento stocastico le sinapsi che cambiano sono estratte a caso ogni volta che un nuovo stimolo viene presentato. In seguito alla presentazione di uno stimolo generico si avranno, in media, qN² sinapsi scelte per effettuare una transizione. Per queste sinapsi, tutto il passato viene dimenticato per adattarsi al meglio al nuovo stimolo. Quando viene presentato lo stimolo successivo, una frazione q delle sinapsi che ricordano lo stimolo precedente sarà estratta per effettuare una transizione, e distruggerà parzialmente l'informazione presente. Solo le restanti (1- q)qN² preserveranno la memoria del primo stimolo. Se P stimoli vengono mostrati alla rete uno dopo l'altro una sola volta, dopo la presentazione di tutti gli stimoli rimarranno solo q(l-ql-¹N² sinapsi con memoria del primo. Una condizione necessaria perché questo stimolo sia richiamabile, è che almeno una sinapsi lo ricordi:
formula. [5]
Come si può vedere dall'ultima disuguaglianza, il numero di memorie possibili è tanto più grande quanto più q è piccola. Invece, se q rimane fissa con l'aumentare di N, il numero di stimoli che la matrice sinaptica è in grado di tenere in memoria è minore di ClogN, con C indipendente da N. La probabilità q non può però diventare troppo piccola, poiché deve cambiare in media almeno una sinapsi per stimolo (qN²> l, ovvero q=k/N² con k>l), da cui si trova che, diminuendo q, al massimo si può arrivare, per N grande, a:
formula [6]
pur mantenendo una traccia del passaggio di tutti gli ultimi p stimoli, il che è una condizione necessaria perché siano richiamabili.
Se gli stimoli presentati sono casuali, ed è bassa la frazione media di neuroni che risultano attivi per ogni stimolo (il livello di codifica), allora solo un sottoinsieme di sinapsi tende a essere modificato. In tal caso la struttura stessa degli stimoli fornisce un ulteriore elemento stocastico per ripartire meglio le risorse tra le diverse memorie. Infatti ogni nuovo stimolo presentato, essendo basso il livello di codifica, sarà molto diverso da quelli precedenti, e dunque tenderà a modificare sinapsi che non venivano utilizzate dalle memorie preesistenti. Ci sono in effetti due estrazioni casuali dietro la modifica di ogni sinapsi: la prima è decisa dalla struttura dello stimolo casuale, che estrae a caso un sottoinsieme di sinapsi candidate a essere cambiate; la seconda è il meccanismo stocastico intrinseco in ogni sinapsi, che effettua una ulteriore sotto selezione delle sinapsi che si adatteranno effettivamente allo stimolo.
Se le probabilità di transizione efficaci, che tengono conto anche della struttura degli stimoli, sono tali da avere un numero medio di potenziamenti uguale al numero medio di depressioni, allora le N² memorie sono non solo presenti nella struttura sinaptica, ma di fatto anche richiamabili. Questo risultato riproduce il risultato classico di D. Willshaw (1969) sulla capacità ottimale.
In una sequenza di singole presentazioni, la memoria corrispondente all'ultimo stimolo presentato è la più facilmente richiamabile. Andando indietro nel passato, la traccia di memoria degli stimoli via via più vecchi si indebolisce, fmché, oltre il P-esimo stimolo nella sequenza, le distribuzioni sinaptiche non sono più richiamabili. Se invece q è così piccola da richiedere molte presentazioni dello stesso stimolo prima che esso sia richiamabile, allora l'ultimo stimolo non è privilegiato, e le P memorie sono tutte sullo stesso piano (Brunel et al., 1998). Ogni stimolo presentato modifica così poco la struttura sinaptica che difficilmente perturba le sinapsi che si sono adattate agli altri stimoli. La frazione di sinapsi che viene modificata per acquisire informazione sul nuovo stimolo è molto bassa, e per questo sono richieste molte presentazioni. Tuttavia è molto bassa anche la frazione di sinapsi che perdono la memoria del passato; alla fine la struttura sinaptica non dipende più dall'ordine temporale in cui queste modifiche vengono effettuate, e la statistica delle correlazioni tra stimolo e struttura sinaptica rimane invariata tra due ripetizioni successive dello stesso stimolo. Si recupera in questo modo la situazione ideale, in cui le risorse di memoria, quantificate dall'efficacia sinaptica, vengono ripartite uniformemente tra tutti gli stimoli che devono essere richiamati.
Reti neurali elettroniche: modelli, simulazioni e realizzazioni hardware
Molta della conoscenza e dell'esperienza acquisita sul comportamento dettagliato di questo tipo di reti deriva dalla loro simulazione al computer, in cui le equazioni che descrivono la dinamica del sistema, cioè l'evoluzione dei neuroni e delle sinapsi, vengono approssimate introducendo passi temporali discreti, in corrispondenza dei quali lo stato del sistema viene ogni volta calcolato e aggiornato. Queste simulazioni costituiscono veri e propri 'esperimenti numerici', in cui si è in grado di riprodurre, fatte salve le molte semplificazioni implicite nel modello, molte caratteristiche degli esperimenti reali, tra cui le registrazioni dei singoli neuroni, le registrazioni multiple, l'uso di diversi protocolli controllati di presentazione degli stimoli.
Questo approccio basato sulle simulazioni, che conserverà comunque, nel futuro, un ruolo essenziale, soffre di due limitazioni. La prima, quantitativa, è legata all'onere computazionale richiesto per simulazioni di reti complesse, in particolare quando si vuole far evolvere nel contempo la dinamica neuronale e quella sinaptica, caratterizzate da scale di tempo molto diverse. Sebbene siano in corso di sviluppo dei metodi di simulazione che alleviano il problema, da questo punto di vista è prevedibile che sistemi neuronali estesi e multimodulari, in grado di realizzare funzioni complesse, rimarranno non trattabili numericamente su calcolatori convenzionali.
La seconda limitazione è di carattere metodologico. Una simulazione non può fornire più informazione di quella contenuta nelle equazioni che definiscono il modello. Il tipo di astrazione necessaria per la definizione matematica del modello può d'altra parte rivelarsi incompatibile con la sua effettiva realizzabilità, sia essa biologica, elettronica o di altro tipo. Con riferimento a quanto esposto precedentemente, una richiesta di profondità analogica infinita per una variabile dinamica (limitata nelle simulazioni solo dalla rappresentazione binaria scelta) o le caratteristiche specifiche imposte a un processo stocastico sono esempi di possibili sorgenti di incompatibilità tra la caratterizzazione matematica di un modello e la sua realizzabilità in un dispositivo reale. È chiaro che, in generale, sarà possibile a posteriori modificare le simulazioni, e tener conto dei vincoli emersi; manca spesso, però, una guida per l'identificazione a priori di tali vincoli. In altre parole, bisogna tener presente che, se da un lato è possibile simulare qualsiasi dispositivo reale, dall' altro non sempre si può far corrispondere un dispositivo reale a un sistema simulato.
Motivazioni per una rete neurale elettronica
Le due limitazioni di cui si è detto rendono desiderabile un approccio complementare alla simulazione numerica di modelli neuronali, basato sulla loro realizzazione elettronica. Da un lato, questo approccio consente in prospettiva la realizzazione di sistemi neurali complessi che interagiscano con l'ambiente in tempo reale; dall'altro, esso svolge una preziosa funzione euristica nell'individuazione dei vincoli a cui i modelli devono soddisfare.
La considerazione contemporanea di questi due aspetti conduce a un genere di hardware neuronale relativamente nuovo, in rapido sviluppo, in cui gli elementi costitutivi della rete sono direttamente ispirati alla loro controparte biologica (Mead, 1989). Questo indirizzo si differenzia in modo marcato da quello, affermato in vari settori applicativi, in cui si realizzano dei coprocessori neurali da affiancarsi ai computer convenzionali, in grado di accelerare significativamente l'esecuzione di una simulazione. La novità dell'approccio ha motivato un neologismo che lo identifica come hardware neuromorfo.
Per quanto riguarda la dinamica neuronale, almeno al livello di descrizione, intermedio tra il macroscopico e il microscopico, al quale i modelli in questione si collocano, sono in gran parte le caratteristiche elettriche del neurone che giocano il ruolo fondamentale: le conducibilità della membrana neuronale rispetto alle diverse correnti ioniche, la capacità della membrana e così via (Katz, 1966; Nicholls et al., 1992). Va ricordato che, a partire dalle equazioni fenomenologiche di Hodgkin e Huxley (che descrivono in modo dettagliato l'emissione del potenziale di azione), fino al modello semplificato di neurone integrate and fire cui si accennerà in seguito, molte caratteristiche funzionali del neurone (e in particolare quelle che si ritengono essenziali ai fini del comportamento collettivo di molti neuroni interagenti) sono state descritte con successo in termini di semplici circuiti elettrici equivalenti. In ultima analisi, comunque, sarà la capacità del modello neurale di produrre comportamenti collettivi in accordo con i dati sperimentali (al livello di descrizione scelto) a fornirne la legittimazione.
La corrispondenza tra i modelli di dinamica sinaptica proposti e i dati sperimentali noti è più difficile da stabilire, e c'è ancora molto lavoro da fare al riguardo, sia dal punto di vista sperimentale che da quello teorico. In questo caso, l'interazione tra le fasi di modellizzazione teorica, di simulazione numerica e di realizzazione elettronica risulta particolarmente feconda.
Il tipo di apprendimento descritto nel paragrafo precedente emerge come versione minimale di una regola di modificazione sinaptica che sia in grado di svolgere i seguenti compiti: soddisfare genericamente un vincolo di realizzabilità, legato a un numero limitato e prefissato di stati stabili discreti per la sinapsi; garantire la località spaziale del meccanismo di apprendimento (la modificazione di una sinapsi dipende solo dall'attività dei due neuroni che essa connette); garantirne la località temporale (la modificazione sinaptica viene indotta dallo stimolo in modo indipendente dagli stimoli precedenti); consentire un'alta capacità di memoria, in funzione del numero di neuroni della rete, adottando un meccanismo stocastico di modificazione sinaptica.
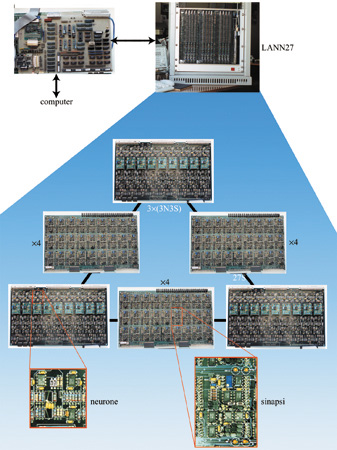
La rete LANN27
Nel seguito descriveremo le prime due fasi di un progetto che si propone di realizzare un sistema neuromorfo integrato su chip, ispirato ai principi di modellizzazione sopra esposti. La prima realizzazione, la LANN27 (Badoni et al., 1995; Del Giudice et al., 1998), è una rete asincrona ad attrattori, costituita da elementi analogici discreti, composta da 27 neuroni e 351 sinapsi simmetriche (quindi completamente connessa), con apprendimento stocastico (fig. 4).
Dinamica dei neuroni. - Data, a un certo istante, una configurazione delle sinapsi Jij (j indica il neurone presinaptico, i il postsinaptico, e Jij = Jij, essendo le sinapsi simmetriche), l'input al neurone generico k è la media, su un breve intervallo di tempo, della somma delle attività Sj(t) degli altri neuroni, pesata dalle efficacie sinaptiche Jkj. Se nell'intervallo di tempo considerato la rete è sottoposta a uno stimolo esterno, questo si traduce in un termine aggiuntivo (e predominante) nell'input al neurone. Il neurone effettua una trasformazione non lineare del suo input totale, determinando il suo stato di attivazione Sk(t). Questa trasformazione è realizzata attraverso amplificatori operazionali, e se il loro guadagno è molto alto (come nelle situazioni che descriveremo), lo stato di attività del neurone può considerarsi una variabile binaria a valori + l o -l.
Poiché la dinamica temporale delle sinapsi è molto più lenta della dinamica neuronale, si può considerare costante la loro efficacia durante il tempo in cui viene mediato l'input al neurone e viene determinato il suo stato di attività. La dinamica collettiva dei neuroni, per una data configurazione sinaptica, si può descrivere qualitativamente: se è presente uno stimolo esterno, questo domina l'attività della rete per tutto il tempo della sua persistenza (tempo di presentazione), che, come vedremo, è anche il tempo utile per l'apprendimento; alla scomparsa dello stimolo, l'attività ricorrente dei neuroni è determinata dalla struttura sinaptica, che ne fissa gli stati di equilibrio (attrattori), la cui esistenza è garantita dalla simmetria delle sinapsi.
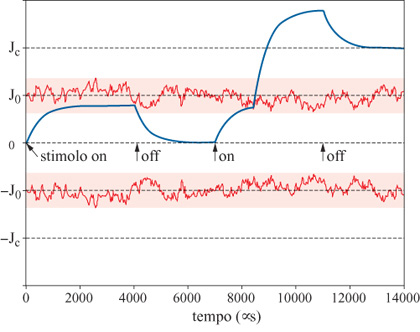
Dinamica delle sinapsi. - La dinamica stocastica delle sinapsi realizza il meccanismo di apprendimento, che modifica gradualmente nel tempo la struttura dei punti di equilibrio della dinamica neuronale (le memorie della rete). Il meccanismo, di tipo hebbiano, è illustrato in figura (fig. 5); esso rappresenta una particolare realizzazione dell'idea già illustrata a proposito della transizione tra gli stati stabili di una sinapsi. Le curve in figura, che fluttuano in modo irregolare intorno ai valori (-Jo,Jo), sono due soglie fluttuanti che realizzano il meccanismo stocastico di transizione; i valori (-Jc,0,Jc) sono i tre stati stabili che la sinapsi può assumere su lunghe scale di tempo. In questo caso, lo stimolo presentato alla rete al tempo iniziale (t = 0) induce lo stesso stato di attività nei neuroni presinaptico e postsinaptico, e questa covarianza tende a potenziare la sinapsi (la curva continua in figura 5 è l'efficacia sinaptica istantanea), che parte dallo stato stabile J = 0.
L'efficacia sinaptica, sotto l'effetto dello stimolo, tende verso un valore asintotico che dipende dall'intensità dello stimolo stesso. Nel caso in figura, durante la presentazione del primo stimolo, la soglia fluttuante rimane sempre al di sopra del valore dell'efficacia sinaptica. In queste condizioni, non si hanno transizioni tra gli stati stabili della sinapsi. Quando lo stimolo viene rimosso, la sinapsi ritorna allo stato stabile di partenza.
Nella figura 5 si può osservare anche la dinamica seguente alla presentazione di un secondo stimolo tale, di nuovo, da potenziare la sinapsi. In questo caso, a causa delle fluttuazioni casuali, la soglia scende al di sotto del valore dell'efficacia sinaptica; questo fatto provoca un istantaneo contributo di potenziamento ulteriore della sinapsi, tale da portarne l'efficacia al di sopra del valore stabile Jc al quale l'efficacia rilassa appena lo stimolo viene rimosso. In questo modo, il secondo stimolo ha indotto la transizione (0 → Jc) della efficacia sinaptica. Il valore Je così raggiunto si manterrà stabile, in assenza di stimoli successivi. In questa dinamica l'efficacia sinaptica assume valori continui determinati dallo stimolo su scale di tempo brevi, mentre assume valori discreti nell'insieme (-Jc,0,Jc) su scale di tempo lunghe.
Nella realizzazione elettronica la presenza di uno stimolo (e il conseguente aumento di attività dei neuroni) viene espressa attraverso un segnale di input ai neuroni, che si aggiunge a quello determinato dall'attività ricorrente, e che entra anche nella determinazione del contributo hebbiano alla dinamica sinaptica. L'intensità di questo contributo influisce sulla probabilità di transizione sinaptica. Esso determina infatti il valore asintotico cui tende il valore analogico della sinapsi (v. figura 5). Nella dinamica sinaptica, inoltre, un meccanismo di adattamento fa sì che l'effetto di uno stimolo che persista per tempi lunghi si attenui gradualmente fino ad annullarsi, in modo che tempi di presentazione molto lunghi non determinino una cancellazione della memoria legata agli stimoli precedenti.
Quando lo stimolo scompare, persiste l'attività riverberante dei neuroni nell' attrattore in cui la dinamica di rilassamento ha portato la rete. Per ogni sinapsi, quindi, permane un' attività presinaptica e postsinaptica potenzialmente in grado di indurre transizioni, sia pure con probabilità molto bassa, se la rete permane a lungo nell'attrattore. Anche in questo caso, un meccanismo di adattamento limita l'effetto a un intervallo temporale limitato.
Il carattere stocastico delle transizioni tra gli stati stabili indotte dagli stimoli è determinato dalla natura casuale delle fluttuazioni delle soglie intorno ai valori -J0 e J0. Come si è visto, un apprendimento stocastico efficiente richiede, in generale, che le probabilità di transizione per le sinapsi siano piccole. Si pone quindi il problema del controllo di queste probabilità nel caso in esame. In linea di principio si può agire su diversi parametri che entrano in gioco nella dinamica, come per esempio l'intensità degli stimoli. Risulta però che, per la maggior parte di essi, le regolazioni richieste, nella regione di probabilità molto piccole, sono molto fini, e questo rende il comportamento della rete instabile e poco controllabile. Ciò costituisce un esempio di come delle specifiche di progetto facilmente formulabili in linea di principio possano incontrare vincoli di implementazione non banali. Una grandezza che si è rivelata idonea per controllare le probabilità di transizione è il contenuto in frequenza delle fluttuazioni delle soglie. In termini qualitativi, è intuitivo che la lunghezza di correlazione di queste fluttuazioni (la memoria del processo stocastico associato) sia legata alla possibilità di ottenere eventi (transizioni) rari. Si è quindi scelto, a livello elettronico, di operare un filtraggio in frequenza di queste fluttuazioni. La frequenza di taglio (insieme alla pendenza) del filtro fornisce un buon controllo delle probabilità di transizione sinaptiche.
Dinamica collettiva della LANN27. - Il sistema ora descritto, pur essendo così limitato nel numero di unità, esibisce un comportamento complesso a causa della retro azione intensa tra le unità stesse. Non si può disporre né di una previsione deterministica della sua dinamica, per la sua natura intrinsecamente stocastica, né di una previsione teorica accurata, poiché il numero di elementi non è abbastanza elevato. D'altra parte, proprio il carattere cooperativo del suo comportamento lo rende molto 'robusto', per esempio, rispetto alle inevitabili disomogeneità elettroniche tra i componenti.
Per illustrare la strategia seguita per estrarre e comprendere il comportamento della rete, riassumiamo innanzitutto le aspettative. La rete deve riflettere, nella sua struttura sinaptica, la statistica spaziale e temporale del flusso di stimoli cui è sottoposta. Essa deve, in particolare: sviluppare in modo non supervisionato rappresentazioni interne robuste per gli stimoli apparsi più di frequente (le basse probabilità di transizione per le sinapsi implicano che siano necessarie molte presentazioni di uno stimolo, affinché sia appreso); poter richiamare gli stimoli appresi in modo associativo (defmire cioè dinamicamente delle classi di stimoli rappresentati dallo stesso attrattore); e, infine, poter dimenticare le rappresentazioni di stimoli non più presenti per tempi lunghi, a favore di stimoli nuovi che entrino nel flusso di input.
Protocolli per lo generazione di flussi di stimoli. - Sebbene la rete sia in grado di adattarsi a un flusso libero di stimoli esterni, è utile, per mettere in luce aspetti specifici del suo comportamento dinamico, adottare opportuni protocolli di presentazione degli stimoli.
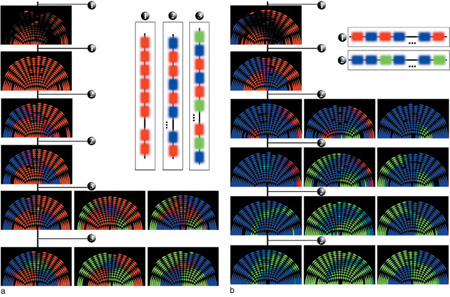
Nel protocollo incrementale si generano a caso 3 prototipi (stringhe di 27 elementi). In una prima fase si presenta ripetutamente alla rete il primo prototipo, con tempi abbastanza lunghi da indurre modificazioni sinaptiche. Quindi si presentano ripetutamente alla rete i primi due prototipi, in ordine casuale, e infine i tre prototipi, sempre in ordine casuale. Questo protocollo, in cui l'ambiente esterno alla rete si arricchisce gradualmente, mette in luce il processo graduale di formazione degli attrattori (cioè delle rappresentazioni interne dei prototipi) in relazione alla diversità di stimoli esterni, e gli effetti che si producono quando la memoria della rete giunge al suo limite di capacità. Nel protocollo di palinsesto si generano 3 prototipi come nel caso precedente. In una prima fase si presentano alla rete, in ordine casuale, i primi due prototipi. Si smette quindi di presentare il primo prototipo, e si presentano ripetutamente in ordine casuale il secondo e il terzo. Questo protocollo misura la capacità della rete di dimenticare: ci si attende che le rappresentazioni interne di stimoli non più presenti nell' ambiente scompaiano gradualmente, a causa (e a favore) di quelle corrispondenti a stimoli nuovi. Nel protocollo di generalizzazione si genera, per ogni prototipo, un insieme di configurazioni (stimoli) ottenute invertendo a caso lo stato di un numero assegnato di neuroni. Si presentano quindi alla rete in ordine casuale queste versioni 'degradate' di tutti i prototipi. Con questo protocollo si intende studiare la fondamentale proprietà della rete di estrarre, da una classe di stimoli simili, una rappresentazione prototipica della classe.
Questi protocolli corrispondono a condizioni di apprendimento in ambienti controllati, in cui si presentano alla rete solo stimoli appartenenti alle classi da memorizzare (i prototipi stessi, o versioni poco perturbate di essi). La capacità di classificazione della rete dovrebbe però mantenersi anche nel caso in cui nel flusso di stimoli appaiano stimoli casuali, scorrelati dalle classi da memorizzare. Ci si attende cioè che la struttura asintotica del paesaggio nello spazio degli stati mantenga valli ampie e profonde in corrispondenza alle classi, anche se piccole valli indotte dagli stimoli casuali ne corrugano il profilo. Allo scopo di controllare queste aspettative, ai tre protocolli sopra descritti si è aggiunto quindi il protocollo rumoroso, nel quale vengono generati uno o due prototipi, e vengono tra loro interposti, nella sequenza in cui vengono presentati, degli stimoli casuali. In questo caso, i prototipi vengono imparati perché presentati molte volte, mentre ogni stimolo casuale produce del rumore che tende a far dimenticare i prototipi.
Per sondare la struttura delle rappresentazioni interne degli stimoli generate in corrispondenza ai diversi protocolli di presentazione si deve verificare, durante le sequenze di apprendimento, la risposta della rete a una varietà di stimoli. Questi stimoli, che chiameremo stimoli di richiamo, devono essere presentati per un tempo abbastanza breve da non indurre a loro volta modificazioni sinaptiche, e devono rappresentare un buon campionamento dello spazio di tutti i possibili stimoli, in modo da fornire una buona descrizione dell'insieme delle risposte della rete.
Riprendendo ancora una volta la metafora del paesaggio, immaginiamo ora di essere in volo al di sopra di questa complicata oro grafia, e di volerne studiare la struttura; una nebbia ci impedisce di distinguere le valli, ma in fondo a ciascuna di esse qualcuno accende una luce, di colore diverso per ogni valle, appena una palla, che noi lanciamo dall'alto, raggiunge il fondo della valle. Un modo ragionevole di ricostruire la distribuzione e l'ampiezza delle valli consisterebbe nel sorvolare l'intero spazio sovrastante il paesaggio, lanciare con regolarità delle palle verso terra, annotando ogni volta la posizione di partenza, e registrare il colore e la posizione della luce che viene accesa in seguito al lancio. Alla fine avremmo una mappa di tutte le posizioni iniziali di lancio, scomposta in regioni colorate che corrispondono al bacino di attrazione di ogni valle.
Il problema che si deve affrontare per ricostruire la struttura dello spazio degli stati della LANN27 è, in linea di principio, abbastanza simile. Il numero di possibili stati (le posizioni di lancio della nostra metafora) da usare come sonde è però enorme, e inoltre l'alta dimensionalità dello spazio degli stati rende difficile una semplice rappresentazione del 'paesaggio'.
Una rappresentazione grafica dello spazio degli stati. - Il problema va affrontato quindi in due fasi: bisogna prima cercare una rappresentazione dello spazio degli stati (a 27 dimensioni) della LANN27 che renda intellegibile la sua struttura, e poi definire delle grandezze in grado di descrivere quantitativamente (e sinteticamente) il processo di classificazione.
L'apprendimento, nel nostro caso, consiste nella creazione di attrattori intorno ai prototipi delle classi. Il monitoraggio del comportamento della rete consiste nel presentarle un numero elevato di stimoli, che costituiscano un buon campione dello spazio degli stimoli possibili, e nel classificare lo stato di attività persistente che segue ognuno degli stimoli. Può trattarsi solo di un campione, perché il numero totale di stimoli possibili, anche per una rete così piccola, è enorme (227).
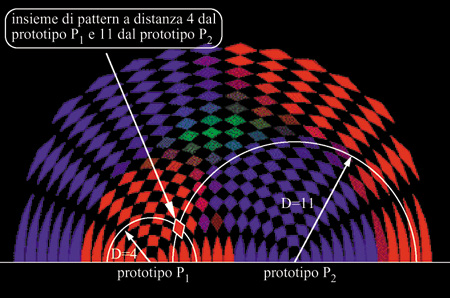
Il risultato del test è una rappresentazione di tutti gli stimoli insieme alloro punto d'arrivo. Considerato che lo spazio degli stimoli è a 27 dimensioni, la rappresentazione grafica della dinamica della rete richiede una proiezione su uno o più spazi a 2 o 3 dimensioni. Una possibilità in tal senso è illustrata in figura (fig. 6). Siccome l'aspettativa è che la struttura dinamica si formi intorno ai prototipi, viene scelto uno spazio di proiezione per ogni coppia di prototipi apparsi nell'apprendimento. A ogni prototipo viene assegnato un colore fondamentale (rosso, verde, blu). Per ogni coppia di prototipi (p) e P₂ nella figura 6) si fissano sul piano due punti rappresentativi, posti a una distanza pari alla cosiddetta distanza di Hamming (numero di neuroni in stati diversi) tra i due prototipi. Una losanga nel piano della figura rappresenta l'insieme di stimoli di richiamo che si trova a una certa distanza da ciascuno dei due prototipi. Il colore della losanga rappresenta la statistica dei punti d'arrivo degli stimoli che partono da questa distanza: ogni stimolo di richiamo che porta la rete verso un attrattore vicino a un dato prototipo dà un contributo alla miscela di colori della losanga con il colore corrispondente a questo prototipo.
Dunque, se per esempio intorno al punto rappresentativo del prototipo rosso si estende un'area rosso vivo, ciò vuoI dire che la maggior parte degli stimoli corrispondenti alle losanghe interne a quest'area provoca, nella rete, DAD vicine a quel prototipo. Questa rappresentazione fornisce una misura del bacino di attrazione del prototipo (la dimensione della valle associata). Analogamente, una zona di colore blu, ma poco intensa, indica un insieme di stimoli che il più delle volte ha provocato, nella rete, DAD lontane dai prototipi, e DAD vicine al prototipo blu negli altri casi. Una zona nera indica un insieme di stimoli che ha prodotto in tutti i casi risposte lontane da tutti i prototipi. Da notare che le losanghe nere (v. figura 6) non sono dovute a buchi nel bacino d'attrazione blu o rosso. Risultano invece dalla struttura discreta dello spazio degli stati, e non corrispondono a nessuno stimolo. Le zone blu e rosse lontane dai prototipi e vicine al bordo corrispondono ad antiattrattori, e sono dovute a una simmetria particolare del modello tra gli stati attivi e quelli inattivi dei neuroni. Durante l'apprendimento si presenta alla rete una lunga sequenza di stimoli secondo uno dei protocolli. Ogni stimolo viene presentato per un tempo sufficientemente lungo da provocare dei cambiamenti sinaptici (stimoli di apprendimento). Periodicamente si effettuano dei cicli di richiamo per controllare il funzionamento acquisito della rete. In figura (fig. 7) è mostrata l'evoluzione degli attrattori con un protocollo di presentazione incrementale. Inizialmente, prima dell'apprendimento, il nero dominante indica una struttura sinaptica scorrelata dai prototipi, tale che le risposte della rete alle prime presentazioni del prototipo (rosso) risultano, in media, lontane da tutti e tre i prototipi. Si vede traccia di questo nella prima istantanea dello spazio degli stati, presa dopo cinque presentazioni del prototipo rosso. Le zone nere, che sono piuttosto estese, non sono dovute solo alla discretizzazione, ma indicano un'effettiva mancanza di bacini di attrazione per i tre prototipi. In seguito viene presentato ripetutamente alla rete solo lo stimolo rosso.
L'attrattore rosso si forma, e il suo bacino copre presto la maggior parte dello spazio. Successivamente il flusso di stimoli viene arricchito: prima il prototipo blu viene presentato insieme al rosso, e infine anche il prototipo verde entra nel flusso di input. Le nuove informazioni competono con le vecchie per creare nella matrice sinaptica una traccia sufficiente a determinare un attrattore. Alla fine, quando il numero di stimoli ricorrenti nel flusso di input supera il limite di capacità della rete, le sinapsi disponibili non sono più sufficienti a mantenere una rappresentazione interna stabile per ognuno di essi. Come vedremo, la LANN27 raggiunge il suo limite di capacità già per p = 3 stimoli. Per tre prototipi la rete è ancora in grado di strutturare il suo spazio degli stati in un numero corrispondente di ampie valli, con il fondovalle vicino ai prototipi. Rispetto ai casi p = l e p = 2 però, oltre a queste valli principali (e per lo più all'interno di esse) compaiono valli minori, corrispondenti ad altrettanti attrattori della dinamica.
La figura 7b illustra inoltre la proprietà esibita dalla rete di dimenticare informazioni già apprese, che però non si presentano più per lungo tempo nel flusso di stimoli, a favore di informazioni nuove. In questo caso si è adottato il protocollo di palinsesto per l'apprendimento. Dopo aver formato attrattori stabili, in seguito alla presentazione ripetuta dei prototipi rosso e blu, la rete reagisce al cambiamento nel flusso di stimoli: il prototipo rosso non compare più e l'attrattore corrispondente tende gradualmente a restringere il suo bacino, mentre vengono presentati ripetutamente i prototipi blu e verde, e si forma l'attrattore corrispondente al prototipo verde, che va a coesistere con il blu.
Capacità di memoria della LANN27. - Abbiamo accennato al fatto che, per p = 3, la rete raggiunge il suo limite di capacità. È per questo che il comportamento della rete in vari scenari di apprendimento è stato descritto solo fino a tre prototipi nel flusso degli stimoli. Una rete piccola esibisce un comportamento complesso intorno al limite di capacità; sia appena sotto, che appena sopra di esso, si presenta un numero elevato di attrattori spuri, con bacini ridotti, accanto a quelli che rappresentano gli stimoli appresi. Questo è quello che si osserva, per esempio, nel modello di Hopfield. Per controllare le caratteristiche dell' apprendimento della rete è essenziale avere un criterio per stabilire il limite di capacità, perché, a questo punto, il comportamento della rete diventa sensibile alle piccole fluttuazioni nella sequenza degli stimoli.
Se la rete è al di sotto del suo limite di capacità, ogni stimolo appreso 'scava' un attrattore, e quando vengono presentati, per richiamo, il prototipo appreso o i suoi vicini, la rete rilassa nella stessa distribuzione di attività neuronale, cioè nello stesso attrattore. Quando anche l'intorno del prototipo non è più compatto, la rete è arrivata al limite di capacità.
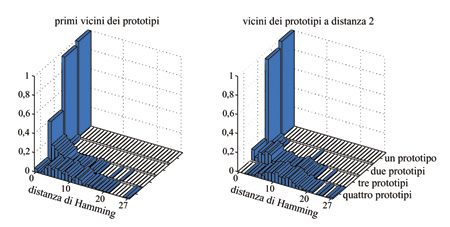
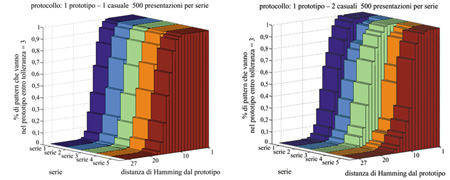
In figura (fig. 8) è mostrata la distribuzione delle distanze massime su molti insiemi diversi di p prototipi (p = l, 2, 3, 4) tra gli attrattori dei prototipi (stimoli appresi) e quelli dei loro primi vicini. Per p≤ 2 i prototipi e i loro primi vicini provocano nella rete la stessa DAD in quasi tutti i casi (99%); la distanza massima è in tal caso nulla, e quindi la rete risulta al di sotto del limite di capacità. Il caso p = 3 è al confine: la coincidenza richiesta vale ancora in un numero elevato di casi (47%), ma molti stimoli che differiscono da un prototipo soltanto per uno stato neuronale portano a un attrattore lontano da quello a cui porta il prototipo stesso: la struttura del bacino d'attrazione si è dunque frantumata. Il caso p = 4 risulta nettamente al di sopra del limite di capacità, in quanto per quasi tutti gli insiemi di prototipi appresi non c'è un attrattore con bacino compatto, come attesta la popolazione di distanze elevate nell'istogramma corrispondente. In figura 8 è anche mostrata la stessa analisi per i vicini dei prototipi posti a una distanza di Hamming pari a 2, in cui si vede che già per p = 3 le distanze di Hamming tra gli attrattori dei secondi vicini e quelli dei prototipi hanno un'ampia dispersione. L'analisi effettuata ci porta dunque a concludere che per p = l e p = 2 si hanno essenzialmente p attrattori, quasi sempre coincidenti con i prototipi. Quando si raggiunge il limite di capacità p = 3, lo spazio degli stati si affolla di attrattori, che tendono ancora a raggrupparsi intorno ai prototipi; in molti casi un prototipo ha ancora lo stesso attrattore dei suoi primi vicini. Per p> 3 gli attrattori si distribuiscono su tutto lo spazio degli stati.
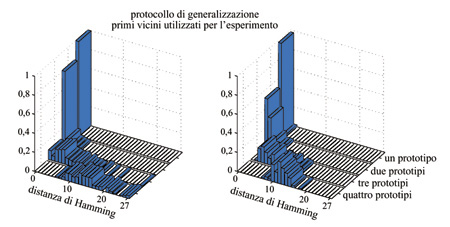
Capacità di generalizzazione e robustezza rispetto al rumore. - Tra le aspettative più importanti per la rete c'è la sua capacità di generalizzazione: la capacità cioè di riconoscere un insieme di stimoli simili come una classe, associando loro un'unica rappresentazione interna. La rete dovrà dunque essere capace di estrarre un prototipo della classe, che potrà non coincidere con alcuno degli stimoli visti durante l'apprendimento, ma dovrà catturare le loro caratteristiche comuni. Nel protocollo di generalizzazione si generano a caso molti insiemi di p prototipi (p = l, 2, 3, 4), e per ogni prototipo si effettua l'apprendimento, utilizzando stimoli scelti a caso tra i primi vicini del prototipo. Nella fase di richiamo si sonda la risposta della rete a tutti i primi vicini dei p prototipi, e ai prototipi stessi; questi ultimi non vengono mai usati durante l'apprendimento.
Per ottenere delle osservabili rappresentative della capacità di generalizzazione si calcola, per ogni p, sia la distribuzione (su tutti gli insiemi di p prototipi) della massima distanza di Hamming tra i prototipi e gli attrattori dei loro primi vicini, sia l'analoga distribuzione delle distanze tra gli attrattori dei prototipi e gli attrattori dei loro primi vicini.
Come mostrato in figura (fig. 9), per p = l e p = 2 l'attrattore dei primi vicini del prototipo coincide con l'attrattore del prototipo stesso: ciò vuol dire che dalla classe di stimoli si è formata una DAD che rappresenta anche il prototipo da cui è stata generata la classe, nonostante questo prototipo non fosse comparso durante l'apprendimento. Un quadro simile risulta se si suppone che la DAD sia simile al prototipo stesso (v. figura 9). Al crescere di p la distribuzione di distanze si allarga, finché, per p = 4, gli attrattori dei primi vicini sono essenzialmente scorrelati dal prototipo. Questi risultati mostrano, con le restrizioni imposte dal limite di capacità, come la rete generi dinamicamente una rappresentazione interna per una classe di stimoli, sulla base delle correlazioni tra di essi.
Come abbiamo osservato sopra, ci si attende che le proprietà di classificazione della rete si mantengano quando si inserisce nel flusso di stimoli un certo numero di stimoli casuali, scorrelati dalle classi. Il basso limite di capacità della rete limita i test quantitativi di questa proprietà.
In figura (fig. 10) riportiamo l'analisi della robustezza rispetto al rumore per il caso p = 1, con 1 = 2 stimoli casuali per ogni presentazione del prototipo. I grafici mostrano la frazione di stimoli di richiamo, situati a varie distanze dal prototipo, che vengono attratti da uno stato a distanza massima 3 ("tolleranza") dal prototipo, in seguito alle sequenze di apprendimento menzionate. I cinque istogrammi in ciascun grafico si riferiscono a cinque diverse scelte del prototipo. Nei casi presentati in figura si hanno attrattori vicini ai prototipi (o coincidenti con essi), con ampi bacini di attrazione degli attrattori.
Nel caso p = 2, invece, l'inserimento di uno stimolo casuale dopo ogni presentazione dei prototipi porta la rete al limite di capacità, e solo nel 20% circa dei casi si sviluppano bacini di attrazione ampi per entrambi i prototipi.
Dalla LANN27 a reti con neuroni impulsanti in VLSI
La LANN27 costituisce, sia nella sua ricchezza che nelle sue limitazioni, un importante dispositivo pilota per diversi motivi. Anzitutto, essa costituisce il primo sistema completamente analogico e asincrono in grado di strutturarsi in modo non supervisionato, adattandosi a flussi arbitrari di stimoli e creando una rappresentazione interna delle loro caratteristiche statistiche in modo associativo. In secondo luogo, tale sistema ha messo in luce le difficoltà, e le possibili strategie risolutive, connesse all'analisi della dinamica di apprendimento in un dispositivo reale. Infine, con le sue limitazioni, ha reso più chiara la strada da percorrere per la realizzazione di reti neurali con apprendimento continuo di maggiori dimensioni e complessità, e più realistiche dal punto di vista biologico.
Tra le limitazioni della LANN27 appare ovvia quella della bassa capacità di memoria, che impone la realizzazione di reti con un numero molto maggiore di neuroni. Questa prospettiva si scontra però con difficoltà in primo luogo tecniche, ma rappresentative anche di questioni di principio.
lnnanzitutto c'è il problema delle dimensioni fisiche della rete. Nella realizzazione circuitale della LANN27 (che è costituita di elementi discreti), lo spazio occupato dalla singola sinapsi eccede largamente quello occupato dal neurone. Questo fatto rappresenta da un lato un ostacolo fondamentale per la costruzione di grandi reti, perché con il crescere del numero di neuroni il numero di sinapsi cresce molto rapidamente (quadraticamente), e dall' altro è indizio di un problema di principio.
Le grandi dimensioni della sinapsi sono dovute principalmente alla sorgente di rumore associata a ciascuna di esse, che sostiene il meccanismo stocastico di apprendimento, e in particolare al circuito che genera e filtra in frequenza il rumore, che a sua volta è necessario per avere basse probabilità di transizione tra gli stati sinaptici stabili. L'esigenza di una sorgente di rumore 'lento' associata a ogni singola sinapsi appare molto problematica da un punto di vista realizzativo, ed è innaturale da un punto di vista neurobiologico, visto che la sinapsi biologica è molto più piccola del neurone.
Inoltre, con reti grandi si presenta il problema dei consumi, che già sono enormi nella rete descritta (circa 200 W). Questa considerazione spinge verso la realizzazione di reti con molti neuroni in elettronica integrata (VLSl, Very Large Scale Integration, integrazione su larghissima scala). Questa scelta, a sua volta, impone nuovi vincoli realizzativi, che implicano scelte diverse in merito agli elementi costitutivi del modello.
Da un punto di vista generale, vi sono poi altre caratteristiche della LANN27 che richiedono di essere riconsiderate in vista di una realizzazione biologicamente plausibile. L'attività della rete dovrebbe riflettere in modo autonomo le diverse condizioni corrispondenti alla presenza dello stimolo (attività molto alta), all'attività selettiva nell'attrattore (di livello medio) e all'attività spontanea (di livello basso). Nella LANN27, come abbiamo visto, la presenza dello stimolo è codificata da un termine aggiuntivo ad hoc nell'input al neurone.
Con i neuroni pseudobinari della LANN27, che assumono valori - 1 o + 1, per ogni sinapsi tutte le quattro coppie possibili di valori presinaptici e postsinaptici inducono un tentativo di modificare l'efficacia sinaptica. Inoltre, illivello di codifica (rappresentato dalla frazione media di neuroni attivi, cioè quelli nello stato + 1, in ogni stimolo) è del 50%. Entrambe queste caratteristiche sono innaturali dal punto di vista biologico: si ritiene che in assenza di segnale presinaptico non vi sia modificazione dell'efficacia sinaptica, e, sperimentalmente, la frazione di neuroni eccitati da uno stimolo in una popolazione corticale di aree associative e di altre aree 'profonde' è molto bassa. Dal punto di vista computazionale, entrambe queste caratteristiche tendono a mantenere bassa la capacità della rete. Esse tendono infatti a rendere più veloce la dinamica sinaptica, aumentando il numero delle sinapsi che tentano di cambiare stato a ogni stimolo, e quindi fanno scomparire più in fretta dalla memoria la traccia degli stimoli precedenti. Questi problemi trovano una soluzione naturale nel passaggio a neuroni che comunichino attraverso impulsi, come in effetti accade nel sistema nervoso reale.
La frequenza di emissione di un neurone che emette impulsi è determinata dall'intensità della corrente ad esso afferente, a sua volta determinata sia dagli impulsi emessi dai neuroni della stessa popolazione, pesati con le corrispondenti efficacie sinaptiche, sia da quelli provenienti dall' esterno. La successione di impulsi prodotti dalla rete appare molto simile a un processo di estrazione casuale di eventi.
In assenza di stimoli, le connessioni tra i neuroni e la corrente esterna sono tali da mantenere nella rete una bassa attività, cioè basse frequenze di emissione (attività spontanea). La presenza di uno stimolo si esprime in un aumento marcato della corrente esterna afferente a un piccolo sottoinsieme di neuroni, che innalzano molto la loro frequenza di emissione. Se lo stimolo è familiare (cioè è già impresso nella struttura sinaptica), alla sua scomparsa la rete rilassa in una DAD, in cui un sottoinsieme di neuroni, selettivo per quello stimolo, continua a emettere a frequenze nettamente superiori a quelle di attività spontanea.
In questo contesto appare un nuovo candidato per la sorgente della stocasticità intrinseca delle transizioni sinaptiche: l'aleatorietà degli intervalli tra gli impulsi emessi dai neuroni presinaptico e postsinaptico. Una sinapsi in grado di sfruttare questa sorgente di stocasticità non avrebbe bisogno di un generatore di rumore, come nel caso della LANN27. Pertanto, il generatore di rumore risulterebbe distribuito su tutta la rete.
Dinamica di neuroni impulsanti e sinapsi plastiche. - Gli elementi di base di un dispositivo integrato ispirato ai principi esposti sono il neurone IF (Integrate and Fire, integra e spara) e la sinapsi plastica. Il neurone IF, quando riceve impulsi da altri neuroni, agisce come un circuito integratore, in cui il potenziale ai capi del condensatore rappresenta la somma dei contributi degli impulsi arrivati. Quando il potenziale supera una certa soglia, viene emesso un impulso, e il potenziale del neurone torna a un valore iniziale, da cui ricomincia il processo di integrazione. Amit e N. Brunel (1997) hanno dimostrato che per la stabilità dell'attività spontanea di una rete di elementi di questo tipo occorre che vi siano due tipi di neuroni: neuroni eccitatori e neuroni inibitori, come accade nella corteccia. I neuroni inibitori devono dare un contributo alla dinamica della rete sufficiente a evitare che gli altri neuroni si eccitino l'un l'altro fino a giungere a un'esplosione incontrollata di attività.
Le sinapsi che connettono i neuroni eccitatori tra loro sono quelle plastiche, e la loro dinamica costituisce un'altra realizzazione del meccanismo di transizioni stocastiche schematizzato in precedenza. La sinapsi ha due stati stabili, ed è stata progettata in modo da avere una rete con neuroni impulsanti che si comporta come un classificatore degli stimoli in ingresso, analogamente a quanto veniva fatto dalla LANN27. Per ottenere questo comportamento, durante la presentazione di uno stimolo che deve essere imparato, l'efficacia deve tendere a essere potenziata quando entrambi i neuroni sono in uno stato di attività elevata (meccanismo hebbiano). Una volta arrivati nello stato potenziato, deve esservi la possibilità di depressione. Nel nostro caso questo avviene quando il neurone presinaptico emette impulsi a frequenza elevata e quello postsinaptico ha solo attività spontanea. Inoltre, quando non vengono presentati stimoli e la rete è in condizioni di attività spontanea, la sinapsi deve preservare la propria efficacia.
Le transizioni descritte devono essere stocastiche, e il meccanismo che le realizza deve essere in grado di sfruttare l'aleatorietà del processo di emissione di impulsi da parte dei due neuroni connessi dalla sinapsi.
Lo schema di funzionamento della sinapsi che è stata realizzata in VLSI analogico e che soddisfa a queste condizioni è illustrato in figura (fig. 11), dove vengono mostrati due casi in cui, a parità di frequenza presinaptica, le diverse frequenze postsinaptiche determinano transizioni dell' efficacia sinaptica verso l'alto (v. figura 11a) oppure verso il basso (v. figura 11b). In alto è rappresentata l'efficacia sinaptica in funzione del tempo durante la presentazione di uno stimolo. La dinamica si svolge nella regione compresa tra i valori 0 e 1, che rappresentano gli stati stabili dell'efficacia sinaptica. In assenza di impulsi, tutti i valori che si trovano sotto la soglia J0 (la linea mediana) vengono attratti verso lo stato basso, mentre i valori che sono sopra la soglia vanno allo stato alto. Lo stato alto costituisce anche il limite superiore per l'efficacia sinaptica, e non può essere superato; analogamente, lo stato basso è il limite inferiore. Quindi questo meccanismo garantisce che, in assenza di impulsi, la sinapsi preservi uno dei due valori di efficacia.
La sorgente hebbiana che spinge l'efficacia verso l'alto o verso il basso risulta funzione delle attività dei due neuroni connessi dalla sinapsi (v. figura 11). L' efficacia riceve una spinta verso l'alto ogni volta che ilneurone presinaptico emette un impulso e il potenziale del neurone postsinaptico si trova al di sopra di una certa soglia θHebb. La spinta è invece verso il basso quando il neurone presinaptico sta emettendo un impulso e il potenziale del postsinaptico si trova al di sotto di θHebb. Quando il neurone postsinaptico emette impulsi a una frequenza elevata, la probabilità che il suo potenziale sia al di sopra della soglia θHebb è molto elevata, e dunque la maggior parte degli impulsi del neurone presinaptico tenderà a spingere l'efficacia verso l'alto. Se per caso si presentano abbastanza eventi di questo tipo in un tempo breve, allora la sinapsi supererà la soglia e transirà allo stato alto. Analogamente, quando il neurone postsinaptico emette a basse frequenze, le spinte attivate dagli impulsi di quello presinaptico saranno prevalentemente verso il basso, permettendo all'efficacia sinaptica di transire allo stato depotenziato. Le transizioni avvengono solo se durante la presentazione dello stimolo arrivano abbastanza impulsi dal neurone presinaptico, il che succede con una certa probabilità (ovviamente minore di 1). Questa natura stocastica delle transizioni sinaptiche è illustrata dal confronto tra le parti sinistra e destra delle figure 11a e 11b, in cui si vede come, a parità di condizioni, le fluttuazioni nell'attività neurale possano consentire o meno l'effettiva transizione.
Nella figura seguente (fig. 12) viene riportato lo schema di un chip aVLSl (analog VLSI, VLSI analogico) che realizza una rete di 21 neuroni lF impulsanti, di cui 14 sono eccitatori e 7 inibitori. Le sinapsi tra neuroni eccitatori sono plastiche, mentre tutte le altre sono fisse. Questa piccola rete pilota è stata realizzata per mettere alla prova i vari elementi e la loro interazione in un regime di correnti estremamente basse. Il passo successivo sarà la costruzione di un chip con alcune centinaia di neuroni e un sistema multichip, per arrivare a una rete di migliaia di neuroni, che già rappresenterebbe un dispositivo d'interesse funzionale e computazionale. Per l'integrazione di un sistema multichip sarà necessario risolvere il problema della comunicazione tra chip (v. il saggio di R. Douglas, M. Mahowald e A. Whatley, in questo volume).
Bibliografia citata
AMIT, D.J. (1989) Modeling brain function: the world of attractor neural networks. Cambridge, Cambridge University Press (trad. it.: Modellizzare le funzioni del cervello, Padova, CEDAM, 1995).
AMIT, D.J., BRUNEL, N. (1997) Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb. Cortex, 7, 237-252.
AMIT, D.J., FUSI, S. (1994) Leaming in neural networks with material synapses. Neural Comput., 6, 957-982.
AMIT, D.J., FUSI, S., YAKOVLEV, V. (1997) A paradigmatic working memory (attractor) cell in IT cortex. Neural Comput., 9, 1071-1092.
BADONI, D., BERTAZZONI, S., BUGLIONI, S., SALINA, G., AMIT, D.J., FUSI, S. (1995) Electromc implementation of an analog neural network with stochastic transitions. Network, 6, 125-157.
BRUNEL, N., CARUSI, F., FUSI, S. (1998) Slow stochastic Hebbian leaming of classes of stimuli in a recurrent neural network. Network, 9, 123-152.
DEL GIUDICE, P., FUSI, S., BADONI, D., DANTE, V., AMIT, D.J. (1998) Leaming attractors in an asynchronous, stochastic electromc neural network. Network, 9, 183-205.
EDELMAN, G.M. (1987) Neural Darwinism: the theory ofneuronal group selection. New York, Basic Books.
FUSTER, J.M. (1973) Unit activity prefrontal cortex during delayed-response performance: neuronal correlates of transit memory. J. Neurophysiol., 36, 61-78.
GOLDMAN-RAKIC, P. (1987) Circuitry of primate prefrontal cortex and regulation of behaviour by representational memory. In Handbook ofphysiology, voI. 5. Bethesda, American Physiological Society.
HEBB, D. (1949) The organization of behaviour: a neuropsychological theory. New York, Wiley.
HOPFIELD, J.J. (1982) Neural networks and physical systems with emergent selective computational abilities. Proc. Natl. Acad. Sci. USA, 79, 2554-2558.
KATZ, LB. (1966) Nerve, muscle, synapse. New York, McGraw Hill.
MEAD, C. (1989) Analog VLSI and neural systems. Reading, Addison-Wesley.
MIYASHITA, Y. (1988) Neuronal correlate of visual associative long-term memory in the primate temporal cortex. Nature, 335, 817-820.
NICHOLLS, J.G., MARTIN, A.R., WALLACE, B.G. (1992) From neuron to brain: a cellular and molecular approach to the function of the nervous system. Sunderland, Sinauer Associates Inc.
NIKI, H. (1974) Prefrontal unit activity during delayed altemation in the monkey. Brain Res., 68, 185-196.
SOMPOLINSKY, H. (1986) Neural networks with nonlinear synapses and a static noise. Phys. Rev. A, 34, 2571. WILLSHAW, D. (1969) Non-holographic associative memory. Nature, 222, 960-962