Apprendimento e controllo degli atti motori
Apprendimento e controllo degli atti motori
Department of Physiology, North Western University Chicago, Illinois, USA
Apprendimento e controllo degli atti motori
La pianificazione e l'esecuzione degli atti motori sono rappresentate da un insieme di sottoprocessi: trasformazione geometrica della traiettoria dell'oggetto da raggiungere da un sistema di riferimento dello spazio esterno a un sistema di coordinate solidale con il corpo; pianificazione del movimento di una parte del corpo; fase di esecuzione che comporta il calcolo del processo dinamico. Per risolvere la complessa dinamica dell'apparato multiarticolare sono state proposte varie ipotesi, brevemente illustrate in questo saggio, le quali indicano che i circuiti del midollo spinale sono organizzati in unità indipendenti, o moduli. L'attivazione di un modulo genera un campo di forza e si possono produrre azioni complesse sovrapponendo i campi generati da moduli attivi simultaneamente. Di conseguenza, i campi di forza possono essere considerati come elementi indipendenti di una rappresentazione del processo dinamico.
Introduzione
Pensiamo a una marionetta: una copia sbiadita di un essere umano, con una testa, un torso, due braccia, due mani, due gambe e due piedi. Ogni parte è congiunta alle altre nel tentativo di riprodurre le articolazioni del corpo umano. In quest'epoca di sviluppo tecnologico, il burattinaio non muove più i fili, ma siede davanti a un pannello di controllo, i cui comandi sono connessi ciascuno a un giunto della marionetta. Ogni comando può attivare cinque posizioni diverse: due per gli angoli estremi e tre per i valori intermedi. La bravura del burattinaio consiste nel padroneggiare i comandi per dar vita alla marionetta. Questa similitudine è un pretesto per introdurre un problema estremamente complesso: un problema, tuttavia, che il cervello umano sembra risolvere senza alcuno sforzo.
Quante posizioni potrebbe assumere una marionetta piuttosto elementare, i cui 13 giunti sono azionati da 13 comandi? La risposta è semplice: 5¹³, dato che ogni comando controlla cinque valori diversi per ognuna delle 13 differenti posizioni della marionetta. Ciò vuoI dire circa un miliardo di posizioni (per essere precisi, 1,2.10⁹). Se si rende la marionetta un po' più complessa, per esempio corredando spalle, mani e piedi di giunti sferici con due angoli, il numero delle posizioni possibili sale a 5¹⁹, cioè più di 10¹³, diecimila miliardi. Per dare un'idea dell'enormità di questa cifra, basti pensare che se ogni neurone contenuto nel cervello umano rappresentasse una delle posizioni possibili del corpo, non basterebbero tutti i neuroni del cervello a rappresentare la gamma completa di posizioni di un singolo individuo.
Questo esempio non inverosimile rispecchia una corrente di pensiero nel campo delle neuroscienze che alcuni considerano riduzionista. In effetti, è allettante riportare le operazioni complesse della mente a semplici azioni rnnemoniche; anche al giorno d'oggi c'è chi afferma che per imparare a muoversi basta codificare ogni movimento utile - per quanto casuale - e ricordarselo quando se ne ha bisogno. Con l'esempio della marionetta si è voluto dimostrare che questo approccio non potrebbe funzionare: l'insieme dei movimenti possibili è infatti troppo vasto per poter essere esplorato in modo adeguato, e tanto meno ricordato, nel corso di un'esistenza.
Quando impariamo a muovere gli arti, il nostro cervello dimostra, di fatto, di conoscere le leggi della fisica. Ciò è valido anche per il cervello dei gatti e delle rane. Sebbene siamo ancora molto lontani dal comprendere i meccanismi di questo processo, negli ultimi decenni sono stati compiuti passi da gigante grazie agli sforzi congiunti di biologi, esperti di informatica, medici, fisici, psicologi e ingegneri. Questo saggio si prefigge di esaminare almeno una parte dei progressi ottenuti. Verranno evidenziate le componenti elementari o, per prendere in prestito un termine della linguistica, i 'moduli' usati dal cervello per generare la competenza necessaria (nelle leggi della fisica) al movimento e all'azione. In particolare, ci interrogheremo su come e quando questi moduli vengono impressi nei circuiti del sistema nervoso centrale.
Per avere un'idea della complessità che sta alla base dell'attività motoria, consideriamo il semplice atto di muovere la mano da una posizione iniziale verso un oggetto da raggiungere. La posizione dell'oggetto viene dapprima codificata dalle cellule della retina; dato che gli occhi si muovono nella testa, e che questa si muove sul corpo, il braccio riesce a raggiungere l'obiettivo solo se l'immagine di quest'ultimo viene definita rispetto al corpo. Mentre si è riusciti a spiegare il problema della codifica del segnale visivo in sistemi di riferimento diversi, come gli occhi, la testa e gli arti in movimento (Andersen et al., 1987), numerose altre problematiche riguardanti la pianificazione e l'esecuzione dei movimenti rimangono irrisolte. Per esempio, non si sa ancora in che modo gli impulsi visivi riescano a provocare i segnali 'motori' che specificano l'ampiezza, la direzione e la velocità di un dato movimento del braccio. Queste componenti fanno parte della pianificazione degli atti motori, e sebbene negli ultimi anni siano state svolte ricerche mirate a comprendere come gli impulsi sensoriali si traducano in questa pianificazione, non è stato ancora possibile ottenere una spiegazione intellettualmente soddisfacente (Georgopoulos et al., 1988).
Quando ci prefiggiamo di muovere la mano da una posizione iniziale A a un punto B nello spazio, vi sono numerose traiettorie che consentono di raggiungere lo stesso obiettivo: non esiste, cioè, una soluzione unica a questo problema motorio elementare. Anche dopo che il sistema nervoso centrale ha stabilito il percorso della mano, lo stesso gesto può essere eseguito con diverse combinazioni di movimenti articolari delle spalle, del gomito e del polso; anche in questo caso, quindi, non esiste una soluzione unica. lnfine, dato che su ogni articolazione si connettono più muscoli, la forza netta che viene generata nella loro attivazione può risultare da diverse possibili combinazioni muscolari. Il problema della trasduzione dei segnali sensoriali in attività motoria è così complesso, perché ancora non riusciamo a incorporare in modo soddisfacente l'apprendimento dei movimenti nelle attuali teorie sulla pianificazione motoria. Nonostante sia ormai certo che il vasto numero di movimenti appresi nel corso dell'esistenza viene memorizzato più o meno permanentemente nelle aree motorie del sistema nervoso centrale, non si sa ancora se la risposta motoria davanti a una situazione completamente nuova usi frammenti di quello che si è già imparato. In questo saggio si accetta il presupposto che l'apprendimento degli atti motori consista nel mettere a punto l'attività di un gruppo relativamente esiguo di neuroni e che queste cellule costituiscano un 'modulo'. La combinazione di diversi moduli potrebbe essere il meccanismo che produce, in modo semplice, un vasto repertorio di azioni.
Il problema computazionale
Secondo le leggi della fisica newtoniana, per imprimere un movimento a una pietra di massa m, bisogna applicare una forza F che sia direttamente proporzionale all'accelerazione desiderata a. Questa legge è definita dall'equazione di Newton:
F=ma. [1]
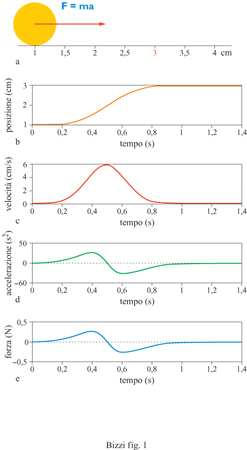
Un movimento può essere espresso come la sequenza di posizioni x che si vuole ottenere dalla pietra in successivi istanti di tempo t. Questa sequenza, detta 'traiettoria', viene rappresentata matematicamente con la funzione x = x( t). Per ricavare la necessaria sequenza temporale di forze, secondo l'equazione newtoniana, bisogna calcolare la derivata prima rispetto al tempo della traiettoria che si intende seguire (velocità) e quindi la derivata seconda (accelerazione). Infine, dall' accelerazione si ottiene la forza desiderata. Questo calcolo è un esempio di ciò che nella robotica viene definito come 'problema dinamico inverso'. (fig. 1). Il problema dinamico 'diretto' consiste nel calcolare la traiettoria risultante dall'applicazione di una forza F(t). La soluzione di questo problema richiede un procedimento di integrazione attraverso il quale il moto della pietra, cioè la funzione x(t), viene ricavato dall'accelerazione nota
a(t) =F(t)/m.
l fisici si trovano quotidianamente davanti a problemi di tipo 'diretto', per esempio, calcolare il moto di una cometa in base alle forze gravitazionali note. Al contrario, il cervello deve risolvere con più frequenza problemi di tipo 'inverso': solitamente riconosciamo oggetti e persone in base alle loro immagini (un problema ottico inverso) e distribuiamo senza sforzo alcuno le forze esercitate dai vari muscoli per muovere gli arti nel modo voluto (un problema dinamico inverso).
Consideriamo il problema di muovere l'avambraccio attivando due muscoli opposti, il bicipite e il tricipite. La traiettoria dell' avambraccio è definita dalla variazione nel tempo di un angolo - l'angolo di flessione del gomito - da un valore iniziale I a un valore finale F. Questa traiettoria è generata dai muscoli che, nel loro insieme, devono applicare sull' articolazione del gomito una coppia M, cioè la forza che tende a imprimere un moto rotatorio a un corpo intorno a uno dei suoi assi; tale forza è data dal prodotto dell'accelerazione angolare del gomito α per l'inerzia dell'avambraccio I:
M=Iα. [2]
Rispetto alla forma normale dell'equazione di Newton, la [2] ha un ulteriore elemento di complessità: la coppia applicata sull'articolazione rappresenta la somma algebrica delle forze esercitate dai due muscoli opposti. Quindi, determinare il contributo di ciascun muscolo comporta una certa arbitrarietà. Si tratta di un esempio di quella ridondanza che caratterizza il sistema motorio e che rende la questione della dinamica inversa un problema malposto. Esempi analoghi si possono riscontrare nella maggior parte dei movimenti naturali del braccio: per esempio, per toccarci con l'indice la punta del naso possiamo usare qualsiasi combinazione di angoli della spalla, del gomito e del polso. Il problema diretto consiste nel ricavare la posizione del dito dagli angoli delle articolazioni; questo comporta calcoli trigonometrici con una soluzione univoca. La stessa cosa non è possibile quando si vogliono trovare gli angoli di un'articolazione che siano compatibili con una determinata posizione del dito: un problema, questo, che ha un numero infrnito di soluzioni.
Naturalmente, nella vita quotidiana si affrontano problemi ben più difficili che non muovere un gomito tra due angoli. Di conseguenza, il cervello deve eseguire calcoli molto più complicati che non risolvere l'equazione newtoniana per una singola articolazione (fig. 2), dato che le equazioni dinamiche che mettono in relazione i momenti delle coppie alla spalla e al gomito (M1 e M2) con le rispettive variabili angolari, le loro velocità e accelerazioni angolari (ω e α) sono decisamente più complesse:
formula [3]
formula [4]
In queste equazioni, le espressioni in parentesi, che moltiplicano le accelerazioni angolari, rappresentano i parametri inerziali. Si noti che questi parametri non sono costanti ma dipendono dall'angolo del gomito, Q2. Le variabili Ij e 1₂ indicano i momenti di inerzia dei due segmenti; mj e m2 le rispettive masse e lj e 1₂ le lunghezze. Le funzioni Bj, B₂, Kj e K₂ rappresentano le forze viscoelastiche passive dei muscoli e dei tessuti connettivi. Le forze attive generate dal sistema di controllo sono rappresentate collettivamente dalla funzione di campo C(Q,t):
C(q,t) =M(q, ω, α). [5]
Dalle equazioni [3] e [4] risulta che l'inerzia del braccio è caratterizzata da molteplici parametri che non sono costanti, ma che dipendono dalla posizione sia della spalla sia del gomito. A questi si aggiungono componenti della forza che dipendono dalle velocità angolari delle due articolazioni. Si deve anche tenere conto del fatto che il movimento di un'articolazione esercita una forza sull'articolazione vicina. Le cose si complicano ulteriormente nel caso in cui aumenti il numero degli angoli in gioco. Occorre domandarsi in che modo il sistema nervoso centrale risolve questi problemi. La risposta non è stata ancora formulata, ma dagli studi di robotica e di neuroscienze computazionali sono emerse diverse ipotesi. l problemi che il cervello deve risolvere per controllare i movimenti sono paragonabili a quelli che un ingegnere deve affrontare nel controllo di un robot (fig. 3). Nonostante le notevoli differenze tra il sistema vertebrato articolare e l'architettura di un robot odierno, il campo delle neuroscienze si è avvalso indubbiamente delle teorie e dei processi che stanno alla base dello sviluppo degli arti artificiali. In passato, per esempio, gli studiosi del cervello sono stati influenzati dal principio della retro azione (feedback).
Controllo a retroazione
Alcuni dei calcoli più complessi associati alla dinamica possono essere evitati grazie alla retroazione, un procedimento per cui un segnale sensoriale comunica la posizione del sistema controllato (per esempio, una mano o un'articolazione) in ogni singolo istante. La posizione attuale dell'arto viene messa a confronto con la posizione da raggiungere; la differenza tra i due valori costituisce la misura dell'errore in quel dato momento. A questo punto, viene prodotta una forza la cui ampiezza è, all'incirca, proporzionale all'ampiezza dell'errore nella direzione della posizione da raggiungere. Si tratta di un metodo di controllo particolarmente efficace grazie alla sua estrema semplicità.
Numerosi meccanismi di retro azione sono stati riscontrati sia nei vertebrati sia negli invertebrati. Il primo a scoprirli è stato C. Sherrington, all'inizio del secolo (Sherrington, 1910). Egli osservò che alla tensione generatadallo stiramento di unmuscolo si contrappone un aumento dell'attività muscolare. Questo 'riflesso miotatico' è causato dall' attività sensoriale che ha origine nei fusi, recettori sensibili alla deformazione delle fibre muscolari (fig. 4). Sherrington avanzò l'ipotesi che i movimenti complessi fossero il risultato di una concatenazione di riflessi miotatici e di altra natura. In questo modo, sequenze di movimento complesse come il ciclo locomotorio potrebbero essere generate da riflessi locali, senza l'intervento di un controllo centralizzato. Successivamente, venne proposta una teoria simile da P.A. Merton (Merton, 1953). Egli suggerì che i comandi centrali, attraverso il sistema fusimotorio avviano il movimento senza attivare direttamente i muscoli, ma innescando un riflesso miotatico mediante la modulazione dell'attività dei fusi muscolari. Entrambe le ipotesi di Sherrington e di Merton hanno cercato di spiegare il movimento come risposta automatica alla retroazione sensoriale e hanno minimizzato quindi il ruolo e l'arbitrarietà dei comandi volontari.
Le teorie di Sherrington sulla combinazione dei riflessi e le ipotesi di Merton sono state invalidate da esperimenti successivi, dai quali è emerso chiaramente che i movimenti possono essere generati anche in assenza di attività sensoriali. Per esempio, E. Taub e collaboratori (1965) scoprirono che le scimmie sono in grado di eseguire svariati movimenti degli arti, anche dopo la resezione chirurgica delle vie che trasportano l'informazione sensoriale dall'arto al sistema nervoso. Non molto tempo dopo, A.B. Vallbo (1973) registrò, nei soggetti umani, le scariche che si propagano lungo i fusi muscolari e le confrontò con l'attivazione dei muscoli rilevata tramite elettromiogramma (EMG) dimostrando, in tal modo, che nei movimenti volontari l'attivazione muscolare non segue ma precede le scariche dei fusi, contrariamente a quanto suggerito da Merton.
Sebbene numerosi riscontri indichino che l'informazione sensoriale non è essenziale alla generazione del movimento, due ulteriori considerazioni suscitano nuovi dubbi sull'efficacia del controllo a retroazione. Il primo riguarda la complessità meccanica degli arti da controllare, il secondo i lunghi ritardi associati alla trasmissione dei segnali di retroazione all'interno del sistema nervoso.
Il problema della complessità meccanica è emerso dai primi studi sul controllo del movimento negli arti con più gradi di libertà. Come è stato già notato, durante il movimento naturale e senza restrizioni, la forza esercitata su un'articolazione non può essere espressa come una semplice funzione dell'accelerazione subita dalla medesima articolazione. Se si dovesse guidare un arto multiarticolare come il braccio con una retro azione lineare, cioè con una forza che sia proporzionale all'errore tra l'angolo voluto e quello effettivo di ogni singola articolazione, si otterrebbero movimenti contorti che, tra l'altro, ritarderebbero il raggiungimento dell'obiettivo. Le interazioni tra le diverse articolazioni, inoltre, comprometterebbero la stabilità dell'arto. Per ottenere prestazioni uniformi nello spazio operativo, un sistema di controllo a retro azione dovrebbe modificare costantemente i parametri di guadagno man mano che l'arto si sposta.
La stabilità dell' arto viene compromessa ulteriormente dal ritardo nella trasmissione delle informazioni sensoriali. Ci vogliono infatti più di 40 ms prima che un segnale generato dai fusi muscolari possa raggiungere i centri motori sopraspinali e altri 40÷60 ms prima che un comando motorio possa essere trasformato in una contrazione muscolare misurabile. L'instabilità causata dal ritardo è ancora più rilevante quando l'arto interagisce con l'ambiente. Per esempio, se il braccio di un robot fosse programmato a premere contro una superficie rigida, un ritardo di 30 ms darebbe luogo a un rimbalzo ripetitivo conosciuto come instabilità di chattering. In questo caso, l'instabilità è dovuta al fatto che il sistema di controllo è in grado di rilevare il contatto solo dopo che questo ha avuto luogo. Il rimbalzo che ne deriva allontana il braccio dalla superficie; il sistema di controllo deve quindi guidare nuovamente il braccio verso la superficie stessa, e così via, dando luogo a una sequenza di impatti.
Un'alternativa al controllo a retro azione sarebbe quella di risolvere in maniera esplicita il problema dinamico inverso, calcolando cioè le forze che i muscoli devono generare per muovere un arto lungo la traiettoria voluta. In teoria, in un arto multiarticolare questo problema dinamico può essere affrontato solo dopo il calcolo della traiettoria degli angoli delle articolazioni, in base alla traiettoria dell' estremità mobile dell'arto, cioè dopo che è stato risolto un problema di inversione cinematica. Dagli studi di robotica condotti alla fine degli anni Settanta e agli inizi degli anni Ottanta è emerso che algoritmi di soluzione del problema cinematico inverso e del problema dinamico inverso possono essere programmati nei sistemi di controllo dei robot con diverse configurazioni geometriche. Basandosi su questi studi, J. Hollerbach e T. Flash (1982) hanno avanzato l'ipotesi che il cervello, nel muovere un braccio con uno scopo preciso, esegua simili calcoli dinamici e cinematici inversi. Dalle loro ricerche è emerso che tutte le componenti delle forze di un'articolazione svolgono un ruolo fondamentale nella generazione dei movimenti. In particolare, i soggetti osservati nell' atto di muovere la mano tra posizioni diverse riuscivano a compensare con accuratezza le interazioni dinamiche tra le articolazioni della spalla e del gomito, producendo così traiettorie rettilinee.
Più recentemente, R.L. Sainburg e collaboratori (1993), A.J. Bastian e collaboratori (1996) hanno fornito ulteriori prove sull' accurata compensazione, da parte del cervello, delle forze di interazione. Sainburg e collaboratori (1993) hanno studiato il movimento di soggetti affetti da una rara neuropatia periferica, che conduce alla perdita completa dell'informazione propriocettiva negli arti superiori e inferiori. Da questi studi è emerso che i movimenti anomali di questi soggetti possono essere attribuiti all'impossibilità di compensare le forze di interazione articolare. A una conclusione simile sono giunti in seguito Bastian e collaboratori (1996) esaminando pazienti affetti da lesioni cerebellari. In conclusione, i risultati raccolti suggeriscono che il sistema nervoso centrale genera comandi motori che rappresentano in modo efficace le complesse dinamiche degli arti multiarticolari; tuttavia è possibile ottenere questa rappresentazione in modi diversi.
Memoria e processi computazionali
Il problema della dinamica inversa si può risolvere anche tramite veri e propri calcoli algebrici, dopo aver rappresentato le variabili quali la posizione, la variazione della velocità, la forza e l'inerzia. Nel 1978, M.H. Raibert propose un metodo di calcolo, basato sull'uso intensivo della memoria, partendo dall'osservazione che il problema dinamico inverso può essere rappresentato come un'operazione mnemonica che associa un gruppo di comandi motori a ciascun valore degli angoli articolari, della velocità angolare e delle accelerazioni angolari. Un approccio primitivo alla dinamica consisterebbe nell'archiviare un valore di forza per ogni singolo valore possibile di posizione, velocità e accelerazione: un metodo computazionale, questo, che gli esperti di informatica definiscono tabella di consultazione o LUT (Look-Up Table). Si tratta di un metodo estremamente semplice, implicito nei primi modelli dell' apprendimento motorio come quelli proposti da J. Albus (1971) e da D. Marr (1969). Tuttavia, questo metodo si dimostra inadeguato quando viene considerata la quantità di memoria necessaria in un ragionevole contesto biologico. Per un braccio che abbia soltanto due angoli articolari e una risoluzione di 10 valori per ciascun angolo, velocità e accelerazione angolari, occorrerebbe almeno un milione di siti di memoria. Per il modello più realistico di un braccio con 7 angoli articolari occorrerebbe una tabella con un numero astronomico di siti, pari a 10²¹.
Il numero di voci della tabella cresce in maniera esponenziale con l'aumentare del numero di componenti indipendenti associati a ogni singola voce; Raibert suggerì di risolvere questo problema scomponendo la tabella in una serie di sottotabelle. Nel caso specifico della dinamica inversa, la forza può essere ottenuta sommando il valore dipendente dagli angoli delle articolazioni e dalle accelerazioni angolari, al valore dipendente da angoli e velocità angolari. Per il braccio a due articolazioni si avrebbero così due tabelle con 10.000 voci ciascuna, mentre per il braccio a 7 articolazioni le due tabelle conterrebbero 10¹⁴ voci. Per risparmiare ancora spazio si potrebbe rappresentare il problema dinamico come la somma di tre elementi, per ognuno dei quali si dovrebbe organizzare una tabella che dipenda unicamente dagli angoli articolari. Ciò si tradurrebbe in tabelle con 100 voci per il braccio a 2 arti colazioni, e a 10 milioni di voci nel caso del braccio a 7 arti colazioni.
Incertezza, stabilità e ipotesi del punto d'equilibrio
Raibert e Hollerbach hanno dimostrato che la dinamica inversa del braccio può essere computata attraverso un numero ragionevole di calcoli e con una quantità altrettanto ragionevole di memoria. Le loro ricerche, tuttavia, non hanno dato prove evidenti che il cervello esegua effettivamente questi calcoli. Dal punto di vista puramente teorico, inoltre, qualsiasi ipotesi fondata sulla computazione della dinamica inversa è insoddisfacente, in quanto non tiene conto delle inevitabili incertezze meccaniche implicite nell'interazione con l'ambiente. Per esempio, si possono avere vistose conseguenze se una forza esterna causa perturbazioni nella traiettoria del braccio. Nel prendere in mano un bicchiere d'acqua, dobbiamo aggiornare il sistema di forze applicate dai muscoli per generare i movimenti del braccio; nell'aprire una porta, occorre tenere conto di un ostacolo, i cardini, la cui posizione nello spazio ci è nota solo in modo approssimativo. Si può concludere, dunque, che la maggior parte dei movimenti viene eseguita in un ambiente meccanico scarsamente prevedibile. Non sarebbe corretto affermare che un dato insieme di attivazioni neuromuscolari corrisponde a un particolare movimento; il movimento generato da quelle specifiche attivazioni è piuttosto il risultato dell'interazione tra le forze muscolari e le dinamiche dell'ambiente. In altre parole, il risultato di un comando motorio è il prodotto di un negoziato tra il sistema di controllo e il suo ambiente. N.Hogan (1985) sviluppò questo concetto dando luogo alla teoria del controllo di impedenza. Le sue ipotesi si ricollegano a studi precedenti di Feldman (1966) e di E. Bizzi e collaboratori (1976). Uno di questi studi fu condotto da A. Polit e Bizzi (1979) su scimmie alle quali era stato insegnato a muovere l'avambraccio verso un bersaglio visivo. Gli animali non erano in grado né di vedere il braccio né di percepirlo sensorialmente, in quanto l'afflusso propriocettivo era stato interrotto chirurgicamente tramite deafferentazione, cioè la resezione delle radici dorsali toraciche e craniali. Polit e Bizzi (1979) scoprirono che le scimmie, nonostante la perdita completa dell'informazione sensoriale, sorprendentemente erano in grado di raggiungere il bersaglio visivo. Non solo, le scimmie riuscivano a eseguire movimenti corretti anche quando il braccio veniva spostato inavvertitamente dal luogo di partenza. Il risultato di questo studio è certamente incompatibile con l'ipotesi secondo la quale la retro azione sensoriale sia indispensabile all'esecuzione di un movimento finalizzato (fig. 5).
Il comportamento della scimmia deafferentata si può spiegare con l'ipotesi che i comandi motori generati a livello centrale modulino l' elasticità e la lunghezza a riposo dei muscoli flessori ed estensori che agiscono sul gomito. Di conseguenza, le proprietà elastiche dei muscoli, simili a quelle di molle agenti in senso opposto, determinano una singola posizione di equilibrio dell'avambraccio. Posizione che viene raggiunta nonostante l'applicazione di perturbazioni esterne, senza bisogno di ricorrere alla retro azione sensoriale. Questo risultato, perciò, porta a una serie di domande sull' esecuzione dei movimenti fmalizzati: è sufficiente regolare semplicemente l'equilibrio statico del braccio in base al bersaglio? Oppure è il comando motorio efferente a determinare l'intera traiettoria come uno spostamento graduale del punto di questo equilibrio? Bizzi e collaboratori (1984) hanno cercato una risposta con un altro gruppo di esperimenti, durante i quali le scimmie deafferentate dovevano eseguire movimenti del braccio in direzione di un bersaglio visivo, ma con la visuale del braccio bloccata da uno schermo opaco. Non appena l'attività elettromiografica segnalava l'inizio del movimento, un motore spostava il braccio direttamente sul bersaglio. Se questa fosse stata la posizione di equilibrio specificata dai comandi del muscolo trasmessi in quell'istante, il braccio non si sarebbe spostato. Invece, è stato osservato un movimento evidente all'indietro verso la posizione di partenza, seguito da un movimento in avanti verso il bersaglio (fig. 6). Questo risultato indica che l'attivazione muscolare non specifica una forza, come suggeriscono i modelli della dinamica inversa, né una posizione fmale da raggiungere. Al contrario, dalla risposta allo spostamento iniziale si può dedurre che l'attivazione dei muscoli produce uno spostamento graduale dell' equilibrio del braccio dal punto iniziale a quello finale. Per ogni istante, l'arto viene attratto da una forza elastica verso il punto di equilibrio. Se nel corso di un movimento il braccio viene sospinto in avanti da una forza esterna, la forza elastica lo richiama indietro, verso il punto d'equilibrio (Bizzi et al., 1979; 1984).
La sequenza delle posizioni di equilibrio prodotte da tutte le attivazioni muscolari durante il movimento è stata definita da Hogan traiettoria virtuale; in tale traiettoria le forze elastiche generate da tutti i muscoli si annullano a vicenda. La traiettoria reale, invece, risulta dall'interazione di queste forze elastiche con altre componenti dinamiche, tra cui l'inerzia dell'arto, le proprietà di velocità e di tensione del muscolo, l'attrito dell'articolazione. Per avere un esempio chiarificatore della differenza tra le due traiettorie, basta pensare a una sfera metallica attaccata all'estremità di un elastico. Quando si sposta l'altra estremità dalla posizione di equilibrio, si genera una forza di richiamo sulla sfera, la cui ampiezza è proporzionale all'allungamento dell'elastico. Dunque, se si muove l'estremità libera dell'elastico lungo un percorso, la sfera seguirà un altro percorso risultante dall'interazione tra la forza elastica e il peso della sfera.
Il rapporto tra la traiettoria reale e quella virtuale è determinato dalle dinamiche del sistema e dalle sue proprietà viscoelastiche, che trasformano un qualsiasi spostamento dalla posizione d'equilibrio in una forza di richiamo. Ovviamente, se l'elastico fosse perfettamente rigido, cioè se il modulo elastico fosse infinitamente grande, la traiettoria reale coinciderebbe con la traiettoria virtuale. Tanto meno un elastico è rigido, tanto più è grande la differenza tra le due traiettorie. In uno studio recente sui movimenti della mano, condotto con l'aiuto di simulazioni al calcolatore, T. Flash e Hogan (1985) hanno esaminato l'ipotesi che il sistema nervoso generi i movimenti del braccio spostando la posizione di equilibrio della mano lungo percorsi rettilinei. Nel 1981, P. Morasso in un esperimento di psicofisica aveva notato che quando a un soggetto veniva richiesto di raggiungere con la mano un bersaglio visivo, questa si muoveva su un percorso più o meno rettilineo tra le posizioni iniziale e fmale. Tuttavia, osservati con maggiore attenzione, questi percorsi hanno rivelato un certo grado di inflessione e curvatura che dipendeva in modo sistematico dalla direzione del movimento e dalla posizione del braccio. Nelle sue simulazioni, Flash ha ipotizzato che le traiettorie virtuali della mano (e non quelle reali, effettivamente misurate) siano invariabilmente e perfettamente rettilinee. Inoltre ha stabilito che la velocità del punto d'equilibrio segua un andamento simmetrico partendo da zero, raggiungendo un valore massimo e ritornando a zero. l risultati della simulazione di Flash hanno evidenziato le più sottili inflessioni delle traiettorie reali osservate da Morasso e da altri. La direzione della curvatura di movimenti simulati in diversi punti dello spazio e con diverse direzioni corrispondevano accuratamente ai movimenti osservati.
È importante sottolineare che i valori di elasticità muscolare usati in queste simulazioni risultavano da misure rilevate non durante il movimento, ma nel momento in cui i soggetti tenevano il braccio a riposo in punti diversi dello spazio (Mussa-Ivaldi et al., 1985). M. Katayama e M. Kawato (1993) riproducendo le simulazioni di Flash con livelli inferiori di rigidità, hanno mostrato che la traiettoria virtuale della mano doveva seguire un percorso molto più complicato per poter riprodurre le traiettorie misurate. Come previsto, la complessità della traiettoria virtuale dipende in modo critico dalle proprietà visco elastiche del sistema neuromuscolare. Attualmente non si è ancora trovata una tecnica accettabile con cui misurare le forze elastiche generate dai muscoli durante il movimento. J. W on e Hogan (1995), tuttavia, si sono avvalsi di un metodo sperimentale diretto per misurare la traiettoria virtuale durante movimenti da punto a punto. Contrariamente alle conclusioni raggiunte da Katayama e Kawato, i risultati di Won e Hogan sembrano confermare che questi movimenti possono essere eseguiti tramite semplici spostamenti del punto di equilibrio. Non si è ancora riusciti a osservare la forma delle traiettorie virtuali nell' ambito di una vasta gamma di movimenti. Se però la forma della traiettoria virtuale fosse un percorso complesso, come emerge dalle simulazioni eseguite da Katayama e Kawato, allora si sarebbe smarrita la semplicità computazionale che sta alla base del concetto stesso di traiettoria virtuale.
Moduli per il calcolo della dinamica: i campi di forza generati dal midollo spinale
La maggior parte delle analisi presentate nelle sezioni precedenti nasce da un'estrema semplificazione della meccanica dell'apparato motorio. Nella formulazione iniziale dell'ipotesi della traiettoria virtuale si presupponeva che la forza che attrae la mano verso il punto di equilibrio istantaneo seguisse la legge della forza elastica di Hooke: la forza prodotta da una molla è direttamente proporzionale alla differenza tra la lunghezza della molla in tensione e quella in situazione di equilibrio. La differenza viene moltiplicata per la costante di rigidità K, cioè:
F=K(x-x0) [6]
In un sistema complesso come il braccio umano, questa relazione lineare è valida solo nelle regioni molto ristrette che circondano il punto d'equilibrio. Man mano che la distanza tra la posizione assunta e quella d'equilibrio supera pochi centimetri, la legge di Hooke si rivela inadeguata a calcolare la forza di richiamo. Occorre, a questo punto, prendere in considerazione una dipendenza non lineare, più complessa, tra forza e spostamento. A questa non linearità contribuiscono diversi fattori, uno dei quali è costituito dalla relazione geometrica tra gli angoli articolari e la posizione della mano. Una variazione modesta dell'angolo della spalla, per esempio di 5°, corrisponde allo spostamento della mano di 2,6 cm, quando questa si trova a una distanza di 30 cm dalla spalla. La stessa variazione di 5°, tuttavia, corrisponde a uno spostamento di 1,7 cm quando la mano è posizionata a 20 cm dalla spalla. A causa di questa variabilità, la legge di Hooke non può essere applicata alle forze esercitate dai muscoli sulla mano: quando lo spostamento della mano raddoppia, lo spostamento della spalla e delle articolazioni del gomito cambia di un fattore che dipende dalla configurazione del braccio. La forza generata dallo stiramento dei muscoli, dunque, non può essere definita da una semplice costante di proporzionalità, K. Un secondo elemento non lineare deriva dalla variazione dell'efficienza geometrica dei muscoli, che si verifica quando cambia l'angolo di un'articolazione. Tale efficienza è espressa dal 'braccio di leva' del muscolo che determina la coppia esercitata sull'articolazione da un'unità di forza muscolare. Il braccio di leva è dato dalla distanza perpendicolare fra la linea d'azione del muscolo e il centro della rotazione articolare; questa distanza va soggetta a cambiamenti continui al variare della posizione del braccio. I cambiamenti del braccio di leva si traducono in modificazioni della costante di rigidità apparente, K. Altri fattori che determinano una dipendenza non lineare tra forza e spostamento derivano dalle proprietà meccaniche dei muscoli. A differenza di quanto si verifica con una molla ideale, il muscolo 'cede' quando viene teso oltre una certa lunghezza: la forza di richiamo comincia a diminuire a causa della minore interazione dei filamenti di actina e miosina. Ne consegue che la rigidità apparente della mano tende a raggiungere un valore limitante, per poi diminuire quando la posizione della mano si allontana ulteriormente dalla posizione di equilibrio.
Sarebbe forse assurdo tentare di dedurre analiticamente l'effetto congiunto di questi fattori sulle forze prodotte dall'apparato motorio. Un'alternativa più realistica consiste nel misurare direttamente le forze generate dall' apparato motorio, in una vasta regione dello spazio, in seguito all'attivazione circoscritta a specifiche regioni del sistema nervoso centrale. Questo approccio è stato adottato in recenti esperimenti elettro fisiologici condotti da Bizzi e collaboratori sulla spina dorsale della rana, durante i quali è stato evidenziato che la stimolazione elettrica e chimica dei circuiti interneuronali del midollo spinale lombare della rana impone distribuzioni particolari dell'attività muscolare dell' arto posteriore. Le contrazioni sinergiche suscitate dallo stimolo generano le forze che dirigono la zampa verso un punto di equilibrio nello spazio. Per misurare la risposta meccanica dei muscoli attivati, Bizzi e collaboratori (1991) hanno collegato la zampa destra di una rana a un trasduttore di forza. Quindi, dopo aver collocato la zampa in una data posizione, hanno stimolato un punto del midollo spinale e registrato la direzione e l'ampiezza della forza isometrica prodotta dallo stimolo sulla zampa. Una stimolazione identica dello stesso sito spinale è stata ripetuta spostando la zampa in 16 posizioni diverse, le cui misure di forza danno luogo a una struttura geometrica nota come campo vettoriale (fig. 7). Nella maggior parte dei casi, la variazione spaziale dei vettori di forza produceva un campo convergente e caratterizzato da un singolo punto d'equilibrio, nel quale la forza si annullava.
Normalmente, l'attivazione di una regione del midollo spinale non produce un campo di forza costante. In questi esperimenti, invece, subito dopo la generazione dello stimolo, i vettori di forza misurati in ogni punto dell'arto cambiavano continuamente nel tempo, e con essi cambiava anche la posizione d'equilibrio: i punti occupati dalla posizione di equilibrio in istanti successivi definiscono una traiettoria. Il campo variabile nel tempo è l'espressione di un'onda meccanica che riassume l'azione congiunta dei muscoli affetti dalla stimolazione. Onde meccaniche dello stesso tipo possono essere usate per descrivere l'operazione dei generatori primari di sequenze temporali (centrai pattern generators) e delle altre strutture neuronali coinvolte nel controllo delle attività motorie. In tutti gli istanti successivi alla generazione dello stimolo, il campo di forza converge verso una posizione di equilibrio.
Nel corso dello studio si sono attivati diversi muscoli della zampa, mentre gli elettrodi usati per la stimolazione venivano spostati in punti diversi del midollo spinale lombare, in direzione rostrocaudale e mediolaterale. Dopo aver definito una mappa della maggior parte delle regioni premotorie nel midollo lombare, si è potuto concludere che esistono almeno quattro aree, dalle quali vengono generati diversi tipi di campi di forza convergenti (fig. 8).
L'aspetto forse più interessante di questo tipo di esperimenti è stata la scoperta che i campi indotti dall'attivazione del midollo spinale seguono un principio di sommazione vettoriale. Mussa-Ivaldi e collaboratori (1994) hanno studiato questo principio eseguendo una prima stimolazione elettrica in un punto del midollo spinale e determinando ne il campo attivo. A questa misura ha fatto seguito una seconda stimolazione in un punto diverso, da cui è stato ottenuto un secondo campo; i due campi sono stati sommati campione per campione. Infine, è stato misurato un terzo campo stimolando simultaneamente entrambi i punti del midollo spinale. Quando i campi delle costimolazioni sono stati confrontati con i corrispondenti campi di sommazione, è stata scoperta un'equivalenza in oltre 1'87% dei casi (fig. 9). Dunque si può concludere che l'attivazione simultanea di due siti spinali conduce alla somma vettoriale dei rispettivi campi di forza.
La somma dei campi di forza implica che le complesse proprietà non lineari che caratterizzano l'interazione fra i neuroni, e fra questi e i muscoli, vengono in qualche modo eliminate. Questo risultato ha condotto a una nuova ipotesi sul movimento e sulla postura, basata sulla combinazione di pochi elementi fondamentali. I pochi campi di forza attivi memorizzati nei circuiti del midollo spinale possono essere considerati come elementi motori primitivi dai quali si possono formare, per sovrapposizione, movimenti molteplici, tramite gli impulsi trasmessi dalle vie sopraspinali. Usando modelli matematici, Mussa-Ivaldi e Giszter (1992) hanno confermato che quest'ipotesi sulla generazione del movimento e della postura ha la competenza necessaria al controllo di un vasto repertorio di atti motori.
I campi vettoriali generati dal midollo spinale sono un chiaro esempio del controllo di impedenza descritto precedentemente. Il campo definisce la forza generata dal midollo spinale in risposta a una posizione imposta all'arto dall'ambiente. Gli esperimenti svolti suggeriscono che i circuiti del midollo spinale (e forse anche quelli di altre aree del sistema nervoso) sono organizzati in unità indipendenti, o moduli. Sebbene ogni modulo generi un campo particolare, si possono facilmente produrre azioni più complesse sovrapponendo i campi generati da moduli attivi simultaneamente. Di conseguenza, questi campi di forza possono essere considerati come elementi indipendenti di una rappresentazione della dinamica. Simulazioni recenti hanno dimostrato che, usando questa rappresentazione modulare, cioè sommando campi di forza convergenti, il sistema nervoso centrale può imparare a riprodurre e a controllare la dinamica di un arto multiarticolare che interagisce con la dinamica dell'ambiente.
Apprendimento motorio: ruolo dei modelli interni
Negli ultimi anni ha guadagnato terreno l'ipotesi secondo la quale l'apprendimento attraverso l'esperienza sia il meccanismo principale con cui si acquisiscono abilità motorie. Questo nuovo approccio deriva in gran parte da studi teorici e sperimentali che cercano di capire i meccanismi dell'apprendimento in modelli di reti di neuroni. Molti di questi studi hanno dimostrato che quando le reti neurali artificiali vengono esposte a ripetuti comandi motori e alle loro conseguenze sensoriali, l'apprendimento di azioni piuttosto complesse si può verificare senza bisogno di una programmazione esplicita. L'apprendimento deriva da una modifica della struttura interna della rete artificiale: più precisamente, da un cambiamento nelle connessioni tra gli elementi della rete.
In base a questi risultati è stata avanzata l'ipotesi che processi simili si verifichino nel sistema nervoso centrale durante l'apprendimento di un atto motorio. Secondo questa ipotesi, l'apprendimento sarebbe il risultato di ripetute esposizioni ai segnali sensoriali provenienti dal movimento degli arti mentre questi interagiscono con l'ambiente. I segnali sensoriali necessari all'apprendimento associativo vengono convogliati nelle aree motorie del sistema nervoso centrale, dove si producono i comandi che provocano l'attivazione dei muscoli. Le azioni generate dall'attività delle aree motorie non sono inizialmente molto precise; un meccanismo di retroazione sarebbe però in grado di produrre una convergenza graduale verso la soluzione corretta. A conti fatti, questo processo iterativo potrebbe condurre a una rappresentazione interna delle azioni attraverso il cambiamento graduale della forza sinaptica dei neuroni delle aree motorie. Qualora l'azione consista nel muovere un arto, il risultato dell'apprendimento sarebbe la formazione di un modello interno della dinamica dell'arto. Secondo quest'ipotesi, il modello interno è iscritto nelle nuove connessioni tra un gruppo di neuroni, l'attività dei quali genera gli impulsi neuronali necessari all'esecuzione dei vari movimenti che sono stati appresi.
I risultati sperimentali ottenuti da R. Shadmehr e MussaIvaldi (1994) hanno dimostrato chiaramente la formazione di modelli interni. Nel corso di un esperimento apparentemente molto semplice, i soggetti dovevano eseguire vari movimenti della mano in presenza di forze esterne, applicate da un robot. I soggetti, impugnando l'estremità libera del robot come puntatore, dovevano raggiungere diversi bersagli visivi. Dato che il campo di forza prodotto dal robot modificava notevolmente la dinamica del braccio, i primi movimenti compiuti dai soggetti erano molto distorti rispetto a quelli analoghi eseguiti senza perturbazioni esterne. Con l'esperienza, tuttavia, la traiettoria della mano nel campo di forza finì per convergere verso la traiettoria prodotta in assenza di campi di forza (fig. 10).
La capacità di compensazione dei soggetti era dovuta all'apprendimento. Per esaminare i cambiamenti neuronali impliciti in questo tipo di apprendimento motorio, Shadmehr e Mussa-Ivaldi (1994) hanno realizzato una semplice manipolazione sperimentale. Dopo che i soggetti hanno imparato a compensare il campo di forza, questo è stato eliminato all'improvviso per la durata di un singolo movimento della mano. Le traiettorie risultanti, definite a 'effetto residuo', erano quasi speculari alle traiettorie osservate quando i soggetti erano stati esposti inizialmente ai campi di forza. Questo fenomeno indica che il campo di forza esterno era stato trasformato dal sistema nervoso centrale in un modello interno, che genera modelli di forza capaci di prevedere, in maniera efficace, le perturbazioni incontrate dalla mano in movimento. Dal momento che queste forze apprese compensavano le perturbazioni applicate dal braccio del robot durante i movimenti del soggetto, si è dedotto che il sistema nervoso centrale programma in anticipo queste forze. Il fenomeno dell'effetto residuo dimostra che queste forze non sono il risultato di una compensazione riflessa dei campi di perturbazione.
È interessante chiedersi quali siano le proprietà del modello interno e, in particolare, se questo modello possa essere esteso a regioni dello spazio in cui non si sia ancora avuta esperienza delle perturbazioni. F. Gandolfo e collaboratori (1996) hanno condotto esperimenti durante i quali veniva chiesto ai soggetti di eseguire movimenti planari tra due obiettivi collocati in una porzione ristretta del piano orizzontale (fig. 11). Il soggetto impugnava l'estremità del robot che veniva usato sia per rilevare la traiettoria che per produrre perturbazioni. Anche in questo caso, come negli esperimenti di Shadmehr e Mussa-Ivaldi, l'adattamento è stato quantificato in base al numero di effetti residui osservati quando venivano interrotte le perturbazioni.
Per poter realizzare la generalizzazione dell'apprendimento, Gandolfo e collaboratori hanno provocato perturbazioni solo nelle traiettorie di un sotto gruppo di direzioni e hanno cercato gli effetti residui in movimenti lungo altre direzioni che non erano state soggette alla perturbazione. L'intensità degli effetti residui ha permesso di quantificare il campo di forza che i soggetti si aspettavano di incontrare durante il movimento sia nelle direzioni di cui avevano avuto esperienza del campo sia in quelle non ancora provate. Gandolfo e collaboratori (1996) hanno scoperto che, secondo le aspettative, esistevano effetti postumi lungo le traiettorie conosciute. Tuttavia, l'intensità degli effetti residui andava riducendosi man mano che la direzione del movimento si scostava dalle direzioni sperimentate. Questo risultato indica che la capacità del sistema nervoso di compensare forze esterne è limitata alle regioni in cui il braccio in movimento ha avuto esperienza di perturbazioni. È significativo che i soggetti siano riusciti in qualche misura a compensare le forze che si erano verificate nelle aree adiacenti.
Gli studi di Shadmehr e Mussa-Ivaldi (1994) e di Gandolfo e collaboratori (1996) hanno dimostrato che i soggetti si adattavano a un ambiente nuovo formando una rappresentazione del campo di forza da essi incontrato mentre eseguivano i movimenti. È possibile che questa rappresentazione lasci un'impronta nella memoria a lungo termine? T. Brashers- Krug e collaboratori (1996) hanno condotto indagini a verifica di tale ipotesi esponendo i soggetti a campi di forza che interferivano in modi diversi con l' esecuzione dei movimenti. Dopo aver eseguito ripetutamente i movimenti, i soggetti hanno imparato a compensare un campo di forze esterne (esperimento A) e a guidare con precisione la mano sulle direzioni da raggiungere. Lo stesso gruppo di soggetti, sottoposto nuovamente 24 ore più tardi allo stesso campo di forze, ha dimostrato non solo di aver conservato la capacità motoria appresa ma anche di riuscire a migliorare l'apprendimento rispetto alla fase precedente. Sorprendentemente, i soggetti hanno mostrato un'abilità maggiore il giorno successivo all'inizio degli esperimenti. Un secondo gruppo di soggetti è stato addestrato il primo giorno con un campo di forze diverso (esperimento B) subito dopo aver eseguito l'esperimento A. Nell'esperimento B il manipolatore produceva forze opposte a quelle applicate durante l'esperimento A. Il secondo giorno, quando è stato esaminato questo secondo gruppo di soggetti sull'esperimento A, Brashers-Krug e collaboratori (1996) hanno scoperto che i soggetti non avevano conservato nessuna delle abilità apprese il giorno precedente durante l'esperimento A; un fenomeno, questo, noto come interferenza retrograda. In uno studio successivo, gli stessi ricercatori hanno scoperto che l'interferenza retrograda decresceva progressivamente nel tempo man mano che, durante il primo giorno, aumentava l'intervallo tra gli esperimenti A e B. Se dopo l'esecuzione dell'esperimento A venivano lasciate passare quattro ore prima che il campo di forze dell' esperimento B fosse appreso, le abilità acquisite durante A erano conservate interamente: in questo caso, dunque, l'apprendimento iniziale si era consolidato (fig. 12). L'aspetto rilevante di questi risultati è che la memoria motoria si era trasformata, con il passare del tempo e senza ulteriori esercitazioni, da uno stato iniziale piuttosto fragile a una condizione più solida.
Dall'insieme di questi esperimenti sono state tratte diverse conclusioni: l) esiste un certo livello di specificità nell'apprendimento di un semplice atto motorio. Il modello interno appreso dai soggetti è limitato a quella regione dello spazio in cui viene fatta esperienza della perturbazione. Le stesse forze esterne sono compensate accuratamente in altre regioni; 2) si verifica un miglioramento dell'azione appresa che non dipende dalla pratica ma soltanto dal passare del tempo; 3) esiste un processo di consolidamento dell'apprendimento che richiede un minimo di quattro ore. Il consolidamento non dipende dall' esperienza ma è un evento generato internamente.
Substrato neuronale dei modelli interni
Si può concepire il modello interno come una nuova disposizione dei contatti sinaptici tra un gruppo di neuroni (fig. 13). Teoricamente, un neurone può appartenere a gruppi diversi, ciascuno dei quali genera un modello interno diverso. Se consideriamo il vasto numero di sinapsi sulla superficie di un neurone, il fatto che questo possa appartenere a più gruppi consente la formazione di innumerevoli modelli interni. Questi si possono intendere anche come entità in grado di riorganizzarsi in gruppi più vasti ogni volta che il corpo deve affrontare attività motorie più complesse. Dal punto di vista fisiologico, è comprovato che l'apprendimento di un semplice atto motorio, come quello descritto nella sezione precedente, comporta la riorganizzazione dei contatti sinaptici tra cellule e, in particolare, lo sviluppo di nuove configurazioni di attività tra le cellule delle aree motorie. Recentemente, B. Benda e collaboratori (1997) hanno osservato (fig.14) la graduale comparsa di attività nei neuroni cortic ali dell'area MI, in scimmie che eseguivano movimenti del braccio contro forze esterne (MI è un'area motoria chiave la cui compromissione interferisce seriamente con la capacità di produrre movimenti). L'attività dei neuroni corticali è stata messa in relazione con le forze che compensano i disturbi esterni. È significativo che gli stessi neuroni, inattivi prima che intervenga la perturbazione, restino poi attivi dopo la sua rimozione, al termine del processo di adattamento. Questo fenomeno è conforme all'ipotesi secondo la quale i neuroni dell' area M l agiscono come elementi di un modello interno responsabile della generazione di forze compensatrici. Risultati analoghi sono stati riportati da S. Wise (1998), che ha usato la stessa tecnica di registrazione di singole cellule, ma con paradigmi di comportamento diversi.
Oltre alla corteccia motoria primaria, è stato notato che altre aree corticali del lobo frontale, in particolare la corteccia premotoria e l'area motoria supplementare, sono coinvolte nella formazione dei modelli interni, sia da sole che in combinazione con l'area MI. In particolare, la corteccia premotoria è coinvolta principalmente nell'apprendimento e nella ritenzione delle risposte visuomotorie (Petrides, 1982; Passingham et al., 1985), mentre l'area motoria supplementare sembra coinvolta soprattutto nella formazione di modelli rappresentanti l'apprendimento sequenziale e condizionale (Mushiake et al., 1991).
Shadmehr e H. Holcomb (1997) hanno dimostrato che gli stadi iniziali di formazione del modello interno di una perturbazione sono accompagnati da un aumento di attività nella corteccia prefrontale. Tuttavia, verso la fine dell'apprendimento, il richiamo cerebro-vascolare rnnemonico del modello interno appreso è accompagnato da un aumento del flusso sanguigno nelle aree corti cali e sotto corti cali come le cortecce motoria e premotoria e il cervelletto. In questo stadio finale si osserva, invece, una diminuzione del flusso nella corteccia prefrontale. Una possibile spiegazione di questo fenomeno è che la corteccia prefrontale è un'area in cui le associazioni sensoriali e motorie vengono archiviate solo per periodi brevi (Fuster, 1989; Goldman-Rakic, 1988). L'aspetto più significativo dell'esperimento di Shadmehr e Holcomb è la dimostrazione che al consolidamento progressivo della memoria motoria corrisponde lo spostamento dell'attività dall'area prefrontale a quella premotoria. Da questo insieme di ricerche è stato possibile dedurre che le aree della corteccia motoria e corticale partecipano entrambe alla formazione dei modelli interni alla base delle competenze motorie. A queste aree si aggiungono anche il cervelletto e alcune regioni specifiche dei gangli della base, come hanno dimostrato S. Grafton e collaboratori (1992) e A. Karni e collaboratori (1995) con l'aiuto della visualizzazione a risonanza magnetica funzionale (fMRI, functional Magnetic Resonance Imaging). I loro risultati suggeriscono che, grazie alla formazione di nuove sinapsi, i circuiti di queste aree potrebbero essere in grado di riorganizzare le proprie caratteristiche funzionali. Secondo W. Greenough e collaboratori (1984), con l'apprendimento motorio i rami dendritici dei neuroni corticali nell'area MI diventano più numerosi, probabilmente per il formarsi di nuove sinapsi sui rami stessi. Si tratta di un'ipotesi plausibile se si considerano le osservazioni recenti del gruppo di H. Asanuma (1991), secondo le quali la stimolazione elettrica del talamo aumenta la densità delle sinapsi nella corteccia motoria.
Oltre alla formazione di nuove sinapsi, altri meccanismi contribuiscono alla plasticità corticale e sottocorticale, modificando a lungo termine l'efficacia delle sinapsi che sono state recentemente attive. Secondo un'ipotesi sostenuta da molti (Bliss e L6mo, 1973; ho, 1982), il potenziamento a lungo termine delle sinapsi (LTP, Long Term Potentiation) e la depressione a lungo termine (LTD, Long Term Depression) costituiscono il meccanismo per cui le modifiche indotte dai movimenti ripetuti dell'arto vengono codificate dalle cellule della corteccia motoria (fig. 15). Quest'interpretazione concorda con i risultati ottenuti da x'Q. Qui e collaboratori (1990), secondo i quali l'azione di blocco esercitata dai recettori di tipo NMDA (N-metil-D-aspartato) impedisce ai movimenti ripetuti dell'arto di stabilire un'attività dipendente dalla plasticità sinaptica.
Modelli interni e organizzazione modulare del sistema motorio
Gli studi presentati suggeriscono che il sistema nervoso centrale sia in grado di rappresentare sia le proprietà dinamiche degli arti sia quelle dell'ambiente con cui essi interagiscono. Questa rappresentazione (modello interno) si fonda su gruppi di neuroni corticali e sottocorticali che formano un'unità funzionale o modulo. Solo di recente si è riusciti a capire i meccanismi tramite i quali il sistema nervoso centrale trasforma in azione un modello interno. Il midollo spinaIe è la struttura chiave di questa trasformazione e, come descritto in precedenza, prove sperimentali hanno dimostrato che i circuiti del midollo spinale sono organizzati in unità o moduli indipendenti. Sebbene ogni modulo generi un campo di forza specifico, comportamenti più complessi possono essere prodotti sovrapponendo i campi generati da moduli simultaneamente attivi. Questi campi di forza possono quindi essere considerati elementi indipendenti di un modello interno della dinamica (fig. 16).
Tramite modelli matematici, Mussa-Ivaldi e Giszter (1992), e successivamente A.V. Lukashin e collaboratori (1996) hanno suggerito che questa teoria sulla generazione del movimento e della postura potrebbe spiegare un vasto repertorio di comportamenti motori. Simulazioni recenti eseguite da Mussa-Ivaldi hanno dimostrato che il sistema nervoso centrale può servirsi di questa rappresentazione modulare, cioè dell'aggiunta di campi di forza convergenti, per imparare a riprodurre e a controllare la dinamica degli arti multiarticolari nel contesto di un ambiente dinamico.
Conclusioni
In questo saggio si è voluto dimostrare che il problema della pianificazione e dell'esecuzione di un'azione visuomotoria può essere diviso in un gruppo di sottoprocessi: una trasformazione geometrica dell'oggetto da raggiungere, da un sistema di riferimento dello spazio esterno a un sistema di coordinate intrinseche solidale con il corpo; la pianificazione della traiettoria; una fase di esecuzione che comporta il calcolo della dinamica del processo. Per risolvere la complessa dinamica dell'apparato multiarticolare, sono state proposte varie ipotesi, tra cui le tabelle di consultazione, la traiettoria del punto d'equilibrio, la combinazione di moduli del midollo spinale e la formazione di modelli interni della dinamica. Questi ultimi, sostenuti da un'architettura che ricorda le reti neurali artificiali, si acquisiscono con l'apprendimento motorio, allo scopo di adattare i meccanismi di controllo ai cambiamenti dovuti alla crescita e alle interazioni con un ambiente variabile. Dal punto di vista anatomico, il substrato neuronale dei modelli interni è così distribuito: la corteccia motoria, i gangli della base e il cervelletto sono strutture connesse che diventano attive, a livelli diversi, durante l'acquisizione delle capacità motorie. La rappresentazione distribuita e adattativa dei modelli interni nell'ambito di queste strutture cerebrali è resa possibile dall' esistenza di meccanismi ben identificati di plasticità neuronale. In questo saggio sono state presentate, inoltre, le prove sperimentali e gli argomenti teorici che suggeriscono la formazione dei modelli interni in aree diverse del cervello ed è stato proposto che le strutture del sistema motorio si presentino sotto forma di frammenti, o moduli. Questi frammenti si manifestano nei campi di forza generati dall' attivazione simultanea di più muscoli. Le conoscenze attuali sul midollo spinale suggeriscono che questa struttura esprima un 'vocabolario' minimo di tali campi di forza. L'aspetto più significativo è che questo vocabolario conterrebbe solo una quantità limitata di termini, nonostante le innumerevoli combinazioni muscolari possibili. Sarà certamente importante capire i criteri che hanno condotto alla formazione di un insieme particolare di campi spinali. Concentrandosi sulla meccanica dei campi di forza, non solo si è trovato un sistema di moduli, ma anche una sintassi molto semplice: i campi possono letteralmente sommarsi tra loro per fornire un vasto repertorio di comportamenti e per generare campi più complessi. Questa proprietà additiva sta probabilmente alla base della nostra capacità di compensare perturbazioni complesse, come è stato evidenziato in molti degli esperimenti esaminati.
Per concludere, il modello interno della dinamica di un arto non è altro che un ulteriore campo in cui le forze generate dall' apparato muscolare vengono messe in relazione con lo stato di moto (posizione e velocità) dell'arto. Sebbene si cominci a far luce sulle strutture generate dagli stadi di uscita del sistema motorio, rimane ancora molto da fare prima che si riesca a capire come facciano le diverse parti del cervello ad apprendere e ad assemblare frammenti diversi e più elaborati di comportamento. La sfida probabilmente non è nuova di per sé: ciò che è nuovo è l'arsenale di strumenti concettuali ed empirici emersi nell'ultimo decennio dallo studio computazionale dell'intelligenza motoria e dalla neurobiologia dell'apprendimento.
Bibliografia citata
ALBUS, J.A. (1971) A theory of cerebellar function. Math. Biosci., 10, 25-61.
ANDERSEN, R.A., ESSICK, G.K., SIEGEL, R.M. (1987) Neurons of area 7 activated by both visual stimuli and oculomotor behavior, Exp. Brain Res., 67, 316-322.
ASANUMA, H., KELLER, A., A. (1991) Neuronal mechanisms for motor leaming in mammalian. Neuroreport, 2, 217-224.
BASTIAN, A.J., MARTIN, T.A., KEATING, J.G., THACH, W.T. (1996) Cerebellar ataxia: abnormal control of interaction torques across multiple joints. J. Neurophysiol., 76, 492-509.
BENDA, B., GANDOLFO, F., CHIANG-SHAN, L., TRESCH, M., DILORENZO, D., BIZZI, E. (1997) Neuronal activities in MI of macaque monkey during reaching movements in a viscous force field. 21' Annual Society of Neurosciences Abstracts, 23, 607-612.
BIZZI, E., ACCORNERO, N., CHAPPLE, W., HOGAN, N. (1984) Posture control and trajectory formation during arm movement. J. Neurosci., 4, 2738-2744.
BIZZI, E., DEV, P., MORASSO, P., POLIT, A. (1978) The effect of load disturbances during centrally initiated movements. J. Neurophysiol., 41, 542-556.
BIZZI, E., MUSSA-IVALDI, F.A., GISZTER, S. (1991) Computations underlying the execution of movement: A biological perspective. Science, 253, 287-291.
BIZZI, E., POLIT, A., MORASSO, P. (1976) Mechanisms underlying achievement of final head position. J. Neurophysiol., 39, 435-444.
BIZZI, E., POLIT, A. (1979) Processes controlling evoked movements. Neuropsychologia, 17, 203-213.
BLISS, T.V.P., LOMO, T. (1973) Long-lasting potentiation of synaptic transmission in the dental area of the anaesthetized rabbit following stimulation of the perforant path. J. Physiol., 232, 331-356.
BRASHERS-KRUG, T., SHADMEHR, R., BIZZI, E. (1996) Consolidation in human motor memory. Nature, 382, 252-255.
FELDMAN, A.G. (1966) Functional tuning of the nervous system during control of movementor maintenance of steady posture. Biophysics, Il, 766-775.
FLASH, T., HOGAN, N. (1985) The coordination of arm movements: An experimentally confirmed mathematical modeI. J. Neurosci., 5,1688-1703.
FUSTER, J.M. (1989) The prefrontal cortex: anatomy, physiology, and neuropsychology of the frontal Iobe. New York, Raven Press.
GANDOLFO, F., MUSSA-IVALDI, F.A., BIZZI, E. (1996) Motor learning by field approximation. Proc. Natl. Acad. Sci. USA, 93, 3843-3846.
GEORGOPOULOS, A.P., KETTNER, R.E., SCHWARTZ, A.B. (1988) Primate motor cortex and free arm movements to visual targets in three-dimensional space: II. Coding of the direction of movement by a neuronal population. J. Neurosci., 8, 2928-2937.
GOLDMAN-RAKIC, P.S. (1988) Topography of cognition: parallel distributed networks in primate association cortex. Annu. Rev. Neurosci., Il, 137-156.
GRAFTON, S.T., MAZZIOTTA, J.C., PRESTY, S., FRISTON, K.J., FRACKOWIAK, R.S., PHELPS, M.E. (1992) Functional anatomy of human procedural learning determined with regional cerebral b100d flow and PET. J. Neurosci., 12, 2542-2548.
GREENOUGH, W. (1984) Structural correlates of information storage in the mammalian brain. A review and hypothesis. Trends in Neuroscience, 7, 229.
HOGAN, N. (1985) The mechanics of multi-joint posture and movement controI. Biol. Cybern., 52, 315-331.
HOLLERBACH, N.J., FLASH, T. (1982) Dynamic interactions between limb segments during planar arm movement. Biol. Cybern., 44, 67-77.
ITO, M. (1982) Mechanisms of motor leaming. In Competition and cooperation in neural nets, a c. di Amari S., Arbib M.A., Berlin-NewYork, Springer Verlag.
KARNI, A., MEYER, G., JEZZARD, P., ADAMS, M.U., TURNER, R., UNGERLEIDER, L. (1995) Functional MRI evidence for adult motor cortex plasticity during motor skill leaming. Nature, 377, 155-158.
KATAYAMA, M., KAWATO, M. (1993) Virtual trajectory and stiffness ellipse during multijoint arm movement predicted by neural models. Biol. Cybern., 69, 353-362.
LUKASHIN, A.V., AMIRIKIAN, B.R., GEORGOPOULOS, A.P. (1996) Neural computations underlying the exertion of force: a modeI. Biol. Cybern., 74, 469-487.
MARR, D. (1969) A theory of cerebellar cortex. J. Physiol., 202, 437-470.
MERTON, P.A. (1953) Speculations on the servo-control of movement. In The spinal cord, a c. di Wolstenholme G.E.W., London, ChurchilI.
MORASSO, P. (1981) Spatial control of arm movements. Exp. Brain Res., 42, 223-227.
MUSHIAKE, H., INASE, M., TANJI, J. (1991) Neuronal activity in the primate premotor, supplementary, and precentral motor cortex during visually guided and intemally determined sequential movements. J. Neurophysiol., 66, 705-718.
MUSSA-IVALDI, F.A., GISZTER, S. (1992) Vector field approximation: A computational paradigm for motor control and leaming. Biol. Cybern., 67, 491-500.
MUSSA-IVALDI, F.A, GISZTER, S., BIZZI, E. (1994) Linear combinations of primitives in vertebrate motor controI. Proc. Natl. Acad. Sci. USA, 91, 7534-7538.
MUSSA-IVALDI, F.A., HOGAN, N., BIZZI, E. (1985) Neural, mechanical and geometric factors subserving arm posture in humans. J. Neurosci., 5, 2732-2743.
PASSINGHAM, R., U. HALSBAND (1985) Premotor cortex and the conditions for movement in monkeys (Macaca Jascicularis). Behav. Brain Res., 18, 269-277.
PETRIDES, M. (1982) Motor conditional associative-leaming after se1ective prefrontal lesions in monkey. Behav. Brain Res., 5, 407-413.
POLIT, A., BIZZI. E. (1979) Characteristics of motor programs underlying arm movements in monkeys. J. Neurophysiol., 42, 183-194.
QUI, X.Q., O'DONAGHUE, D.L., HUMPREY, D.R. (1990) NMDA antagonist blocks plasticity of motor cortex maps induced by passive limb movement. Soc. Neurosci. Abstr., 16, 422.
RAIBERT, M.H. (1978) A model for sensorimotor control and learning. Biol. Cybern., 29, 29-36.
SAINBURG, R.L., POIZNER, H., GHEZ, C. (1993) Loss of proprioception produces deficits in interjoint coordination. J. Neurophysiol., 70, 2136-2147.
SHADMEHR, R., HOLCOMB, H. (1997) Changing activations in the prefrontal cortex during the time-dependent phases of motor memory formation. J. Neurosci.
SHADMEHR, R., MUSSA-IVALDI, F.A. (1994) Adaptive representation of dynamics during leaming of a motor task. J. Neurosci., 14, 3208-3224.
SHERRINGTON, C. (1910) Flexion-reflex of the limb, crossed extension and reflex stepping and standing. J. Physiol., 40, 28-121.
TAUB, E., BACON, R.C., BERMAN, AJ. (1965) Acquisition for a trace-conditioned avoidance response after deafferentation of the responding limb. J Comp. Physiol. Psychol., 59, 275-279.
VALLBO, A.B. (1973) The significance of intramuscolar receptors in load compensation during voluntary contractions in man. In Control of posture and Iocomotion, a c. di Stein R.B., Pearson K.G., Smith R.S., Redford J.B., New York, Plenum Press, pp. 211-226.
WISE, S., MOODY, S., BLOMSTROM, K., MIST, A (1998) Exp. Brain Res., 121, 285-299.
WON, J., HOGAN, N. (1995) Stability properties ofhuman reaching movements. Exp. Brain Res., 107, 125-136