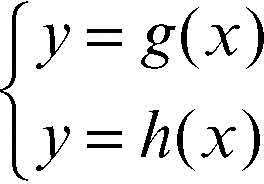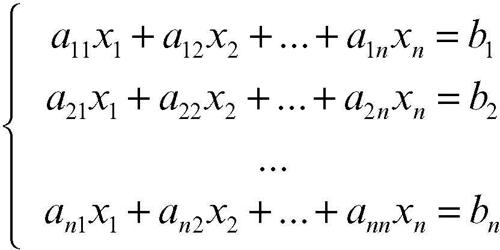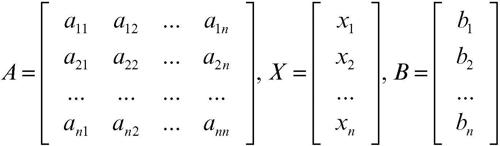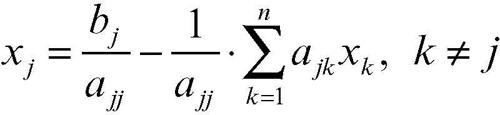approssimazione
approssimazione
approssimazione (di una soluzione) soluzione di un’equazione – o di un sistema di equazioni – ottenuta attraverso l’utilizzo di metodi numerici e contenente un errore che può essere reso trascurabile mediante il raffinamento del procedimento adottato. Non sempre, infatti, sono disponibili formule esplicite per determinare le soluzioni di problemi contenenti un’equazione o un sistema di equazioni. In tali casi si possono ricercare soluzioni approssimate attraverso opportuni metodi algoritmici che, a partire da un valore iniziale, e mediante procedimenti iterativi, ottengono via via risultati sempre migliori. I valori ottenuti sono approssimazioni successive della soluzione cercata e il procedimento termina quando la differenza tra due successive approssimazioni diventa o trascurabile rispetto al problema in esame o minore di un valore predefinito come sufficiente per una buona rappresentazione della soluzione.
Ricerca della soluzione approssimata di un’equazione ƒ(x) = 0
Si considera il problema equivalente della ricerca degli zeri della corrispondente funzione y = ƒ(x) e si procede in due fasi: a) determinazione degli intervalli della variabile indipendente x nei quali il grafico di ƒ(x) ha una sola intersezione con l’asse delle ascisse (e conseguentemente l’equazione ha una e una sola soluzione); b) ricerca, all’interno degli intervalli così determinati, della soluzione dell’equazione ƒ(x) = 0. Il primo problema che si pone è, quindi, quello della separazione delle soluzioni, cioè la determinazione di un intervallo chiuso [a, b] in cui l’equazione abbia una e una sola soluzione. Allo scopo si utilizzano alcuni teoremi dell’analisi matematica:
• il teorema di esistenza degli zeri (se la funzione ƒ(x) = 0 è continua nell’intervallo [a, b] e assume negli estremi valori di segno opposto, cioè ƒ(a) · ƒ(b) < 0, allora esiste almeno uno zero all’interno dell’intervallo considerato);
• i due teoremi di unicità della soluzione di un’equazione: il primo afferma che, verificate le ipotesi del teorema di esistenza degli zeri, se y = ƒ(x) è derivabile una volta in (a, b) e se ƒ′(x) mantiene lo stesso segno nel medesimo intervallo, allora esiste una e una sola soluzione in (a, b); il secondo generalizza il risultato, basandosi sulla costanza di segno della derivata seconda e generalizza altresì l’ipotesi restrittiva del primo teorema relativa alla necessità del carattere monotono di ƒ(x).
I due teoremi sull’unicità della soluzione sono utili quando i calcoli delle derivate prime e seconde sono semplici e quando è facile calcolare il loro segno, come accade nelle funzioni polinomiali. Nel caso di funzioni algebriche più complesse o di funzioni trascendenti, il calcolo delle derivate e lo studio del loro segno può comportare difficoltà. Si può allora ricorrere a opportune trasformazioni della funzione e alla sua rappresentazione grafica. Se è possibile riscrivere la funzione y = ƒ(x) come differenza di altre due funzioni ƒ(x) = g(x) − h(x), si ha che ƒ(x) = 0 ⇔ g(x) = h(x). Quest’ultima equazione può essere interpretata come l’equazione risolvente del sistema
Risolvere il sistema vuol dire cercare le intersezioni tra le due curve che sono i rispettivi grafici delle due funzioni; le ascisse dei punti di intersezione danno le soluzioni dell’equazione ƒ(x) = 0. È così possibile determinare approssimativamente gli intervalli in cui tali soluzioni cadono; nel caso in cui una delle due funzioni, g(x) o h(x), è lineare, si tratta di determinare le intersezioni tra una retta e una curva.
Accertate le ipotesi del teorema di esistenza e unicità della soluzione, si possono poi utilizzare i metodi numerici più opportuni: il metodo di → bisezione, il metodo delle → secanti (o delle corde), il metodo di → Newton (o delle tangenti), il metodo dell’→ attrattore.
Ricerca della soluzione di un sistema lineare
Oltre ai metodi diretti come il metodo di → Cramer o il metodo di eliminazione di Gauss (→ Gauss, metodo di), esistono metodi iterativi che consentono di trovare una soluzione approssimata del sistema lineare. Tali metodi risultano particolarmente utili quando il numero delle incognite è molto grande. Si consideri il caso di un sistema di equazioni lineari
in cui il numero di equazioni sia uguale al numero delle incognite. In forma matriciale il sistema si può scrivere nella forma più compatta AX = B, dove A è la matrice quadrata dei coefficienti, X è il vettore delle incognite e B è il vettore dei termini noti:
Esplicitando le incognite, da ogni equazione del sistema si ottiene
Data una n-pla approssimata di soluzioni
applicando un metodo iterativo si ottiene una nuova n-pla X(1) e continuando il procedimento si ottiene via via una successione di soluzioni approssimate X(0), X(1), X(2), ..., X(k). Se esiste il
allora la successione converge e tale limite è la soluzione del sistema. Il valore iniziale della prima n-pla non è rilevante. Infatti essa può essere approssimata anche grossolanamente, per esempio scegliendo la n-pla nulla, perché, se la successione è convergente, lo è per qualsiasi scelta di valori iniziali: la n-pla, per così dire, “si autocorregge”.
Per la ricerca della soluzione approssimata di un sistema di equazioni lineari sono usati principalmente due metodi: il metodo di → Jacobi, e il metodo di → Gauss-Seidel.
Ricerca della soluzione approssimata di una equazione differenziale
Esistono molti metodi, che si differenziano per le modalità di esecuzione e per la tipologia di equazione cui si riferiscono. Supponendo verificate tutte le ipotesi di esistenza e unicità della soluzione dell’equazione differenziale, si possono applicare molti metodi numerici approssimati, i più importanti dei quali sono il metodo di → Eulero e i metodi di → Runge-Kutta, con tutte le loro varianti. Il metodo di Eulero si applica alle equazioni differenziali del tipo: y′ = ƒ(x, y) con y = y(x) definita nell’intervallo [a, b], con la condizione iniziale y(x0) = y0. I metodi di Runge-Kutta (più che di un singolo metodo si tratta di una “famiglia” di metodi) sono tecniche numeriche per risolvere le equazioni differenziali del tipo y′ = ƒ(x, y) con y = y(x), con la condizione iniziale y′(x0) = y0, usando un’approssimazione al second’ordine (per un approfondimento, si veda anche → Heun, metodo di).