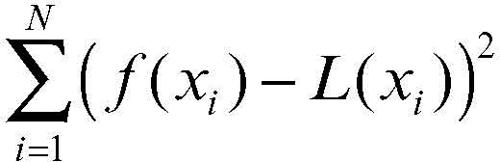approssimazione

approssimazione

approssimazione (di una funzione) sostituzione di una data funzione con un’altra funzione più semplice da studiare e il cui grafico si discosta dal primo in modo trascurabile almeno localmente, cioè in un intorno di un punto in cui si effettua l’indagine. Più in generale, l’approssimazione di una funzione è un metodo per esprimere la dipendenza funzionale tra due grandezze variabili x e y, di cui si abbia una tabella di valori corrispondenti, spesso individuati a partire da una serie di misure effettuate, attraverso una formula che rappresenti in modo non esatto, ma sufficientemente affidabile, tale dipendenza. Attraverso tale formula è possibile calcolare con buona affidabilità i valori della funzione in corrispondenza di valori della variabile per i quali non si abbiano dati certi (per esempio, misure effettuate). Naturalmente per approssimare l’andamento di una funzione è possibile utilizzare funzioni lineari, funzioni polinomiali o altre meno elementari ed è importante stabilire quanto i valori noti si discostino da quelli ottenuti attraverso la funzione approssimante.

Storicamente per risolvere problemi di questo tipo, si sono costruite e utilizzate tavole numeriche che, per un insieme di valori della variabile indipendente x, forniscono con buona approssimazione i corrispondenti valori della funzione ƒ(x) (per esempio, le → tavole logaritmiche o le → tavole trigonometriche). Le tavole risultano più affidabili e utili quanto più vicini sono tra loro i valori considerati delle x. Anche se i computer hanno risolto almeno apparentemente il problema, per la loro possibilità di considerare numeri molto grandi di punti tra loro molto vicini, rimangono comunque oggetto di analisi l’attendibilità del risultato fornito dal calcolo automatico e le modalità con cui viene calcolato il valore della funzione. Esistono metodi numerici che, determinando il valore approssimato di una funzione in un dato punto, hanno carattere locale, cioè l’approssimazione è valida esclusivamente in un intorno del punto considerato: per esempio, rientra in questa categoria l’approssimazione di una funzione con il suo polinomio di → Taylor. Altre forme di approssimazione hanno invece carattere globale, come l’interpolazione lineare, che sostituisce il tratto di curva tra due punti con un tratto rettilineo e come, più in generale, tutte le interpolazioni polinomiali.

Queste considerazioni valgono per gli ambienti di calcolo numerici, che caratterizzano in generale gli algoritmi con cui opera un automa esecutore. Esistono tuttavia procedure radicalmente diverse, di tipo non numerico, ma simbolico; esse trasformano formule e manipolano simboli sulla base di un insieme di regole grammaticali, riducendo drasticamente gli errori e la loro propagazione nei calcoli.

Sul piano teorico, ha interesse il problema della migliore approssimazione lineare che può essere enunciato come segue: dati un elemento v di uno spazio vettoriale normato S, un sottospazio V di dimensione finita n, e una base {v₁, ..., v_n} di V, determinare tra tutte le n-ple di coefficienti (a₁, ..., a_n) quella (â₁, …, â_n) per cui è minima la quantità

Se tale n-pla esiste, l’elemento â₁v₁ + ... + â_nv_n è detto migliore approssimazione lineare di v in V.

Lo studio di un problema di migliore approssimazione lineare si articola in vari punti: a) la dimostrazione dell’esistenza di una migliore approssimazione e della sua unicità (l’esistenza può essere provata in generale, l’unicità è invece legata alla scelta della norma e della base in V); b) la scelta della norma, che dipende dall’uso che si deve fare dell’approssimante; c) la scelta della base, dettata generalmente dalla natura della funzione assegnata; d) la caratterizzazione della migliore approssimazione, ossia la determinazione di alcune proprietà particolari di cui essa gode; infine e) il calcolo effettivo.

Nel caso di una funzione ƒ reale di variabile reale, si pone il problema di approssimarla in forma di combinazione lineare di funzioni più semplici, cioè nella forma

in cui la famiglia v₁(x), ..., v_n(x) si suppone densa in uno spazio opportuno X in cui si approssima ƒ, e si vuole che ‖E_n‖_X → 0. Le famiglie di funzioni v₁(x), ..., v_n(x) più usate per l’approssimazione sono i polinomi algebrici, i polinomi trigonometrici, esponenziali e complessi. Il caso v_i(x) = xⁱ rientra nella cosiddetta approssimazione polinomiale, che consiste nell’approssimazione di una funzione mediante un polinomio scelto all’interno di una certa famiglia di polinomi, per esempio il polinomio interpolatore di Lagrange (→ Lagrange, interpolazione di). In generale, oltre alla scelta dello spazio X si fissano dei criteri di approssimazione in cui si richiede che la funzione approssimante a₁v₁(x) + ... + a_nv_n(x) abbia certe caratteristiche desiderate. I criteri di approssimazione più utilizzati sono: l’assegnazione delle derivate in un punto, l’interpolazione, l’errore di norma minima e le funzioni ortogonali.

L’assegnazione delle derivate in un punto si effettua in generale con polinomi e quella che si ottiene è la formula di Taylor (→ Taylor, polinomio di). L’interpolazione si effettua in generale con polinomi e consiste nell’imporre che il valore della combinazione lineare a₁v₁(x) + ... + a_nv_n(x) coincida con quello della funzione in un certo numero di punti assegnati; si può eventualmente assegnare nei punti anche il valore di un certo numero di derivate (→ Hermite, problema di). L’errore di norma minima consiste nello scegliere l’approssimazione il cui errore abbia norma minima; nel caso della norma L², questo dà luogo ai polinomi di → Fourier. Il criterio delle funzioni ortogonali consiste nell’approssimare ƒ con i primi n termini di uno sviluppo in serie di funzioni ortogonali (in genere, rispetto al prodotto scalare in uno spazio L²); fornisce la migliore approssimazione nella norma associata al prodotto scalare scelto; inoltre permette di operare sia mediante polinomi ortogonali, sia mediante funzioni trigonometriche. Nel caso in cui si cerchi una funzione L(x) = a₁v₁(x) + ... + a_nv_n(x) che renda minima la quantità

nel caso continuo, oppure la quantità

(con x₁, ..., x_n valori fissati) nel caso discreto, si parla di migliore approssimazione L² o ai minimi quadrati (metodo dei → minimi quadrati).