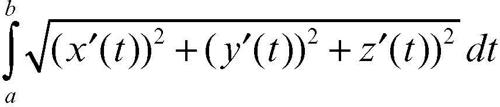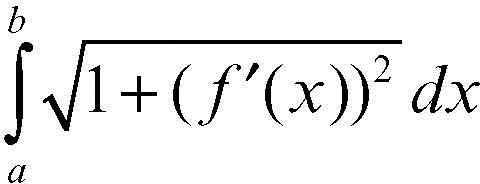arco di curva, lunghezza di un
arco di curva, lunghezza di un
arco di curva, lunghezza di un numero reale non negativo che misura un tratto di curva in rapporto alle unità di misura rettilinee. Per un arco di circonferenza, il problema si riduce alla determinazione dell’ampiezza dell’angolo al centro che individua l’arco: la sua lunghezza è infatti αr, essendo r il raggio e α l’angolo al centro associato, misurato in radianti. Non esistono invece formule generali per misurare archi di curve qualunque e il problema rimanda a quello della possibilità di rettificare la curva di cui l’arco fa parte, cioè di determinare un segmento rettilineo di lunghezza supposta uguale a quella dell’arco (→ rettificazione). Ogni curva non rettilinea ha infatti una sua forma particolare, non necessariamente riconducibile alla somma di lunghezze di segmenti rettilinei, gli unici per i quali è effettivamente stabilito un criterio di confronto e rapporto con una unità di misura dello stesso tipo. Il problema si risolve a partire dall’intuitiva considerazione del fatto che se la curva è «regolare» in ogni suo punto (cioè, tecnicamente, è ovunque differenziabile) allora essa può essere in prima istanza approssimata da una linea spezzata poligonale formata da segmenti consecutivi.
All’aumentare del numero di segmenti (e quindi al diminuire della lunghezza di ognuno di essi) la linea spezzata assume una forma sempre più «vicina» a quella dell’arco di curva. Se in R3 l’arco di curva è dato in equazioni parametriche x = x(t), y = y(t), z = z(t), con a ≤ t ≤ b, la lunghezza di un tale arco di curva si definisce come l’estremo superiore dell’insieme numerico costituito dalle lunghezze di tali spezzate poligonali, aventi i vertici nei punti della curva corrispondenti a una qualunque scomposizione dell’intervallo base [a, b] in un numero finito di intervalli a due a due privi di punti interni in comune. Se tale estremo superiore esiste finito, la curva, in tale intervallo, si dice rettificabile. Se la curva è regolare in ambiente R3, all’interno dei valori estremi a e b del suo parametro t, la sua lunghezza (la lunghezza del suo arco) è:
dove x′(t), y′(t), z′(t) sono le derivate prime delle corrispondenti funzioni che compaiono nelle equazioni parametriche. Se la curva di cui fa parte l’arco è piana ed è il grafico di una funzione y = ƒ(x), allora la lunghezza dell’arco di estremi x1 = a e x2 = b è data da
dove ƒ′′(x) è la derivata della funzione di cui la curva è grafico.