arcotangente

Enciclopedia della Matematica (2013)

arcotangente


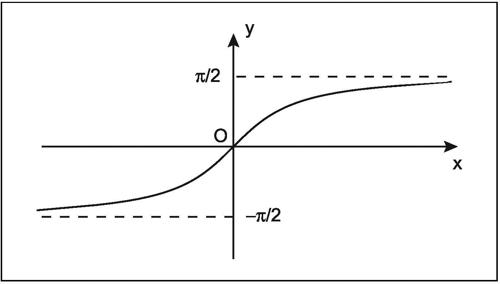
arcotangente funzione inversa della funzione → tangente ristretta all’intervallo (−π/2, π/2); si denota con il simbolo arctan o tan−1. Si ha

formula

L’arcotangente è una funzione dispari (il suo grafico è cioè simmetrico rispetto all’origine) e strettamente crescente; ha inoltre due asintoti orizzontali costituiti dalle rette di equazioni y = ±π/2. La sua derivata è:

formula
ARCOTANGENTE

Vedi anche
tangente In geometria, si dice di ente (retta, linea, superficie ecc.) che abbia un particolare rapporto spaziale con altro ente della stessa natura, definito caso per caso e che riguarda comunque l’intersezione dei due enti considerati (che si dicono anche tra loro t.). In particolare, retta t. a una curva in ... James Gregory Matematico e ottico (Aberdeen 1638 - Edimburgo 1675); prof. di matematica all'univ. di Edimburgo e membro della Royal Society; fu a Padova dal 1664 al 1667. Pubblicò opere di geometria, usando dapprima i metodi classici, poi il metodo degli indivisibili; diede lo sviluppo in serie della funzione arcotangente; ... anàlisi infinitesimale (o càlcolo) Parte della matematica (detta anche semplicemente analisi matematica) i cui metodi e sviluppi sono fondati sull'operazione di passaggio al limite. Suoi iniziatori sono considerati nel 17° sec. I. Newton e G.W. Leibniz, tuttavia ha avuto il suo sviluppo solo in seguito alla definizione rigorosa ... sistèma di riferiménto Schematizzazione geometrica dello spazio al quale si riferisce un ente o fenomeno (per es. il moto di un corpo); più precisamente, insieme di elementi (origine, assi coordinati, unità di misura), che permette di associare a ogni ente geometrico (punto, retta ecc.) uno o più enti analitici (coordinate, ...
Tag
Altri risultati per arcotangente
  • arcotangente
    Enciclopedia on line
    In trigonometria, si dice a. di x l’arco la cui tangente trigonometrica è x; simbolo: arctangx (o arctgx). La funzione y=arctangx è quindi funzione inversa della funzione circolare ‘tangente’.
Vocabolario
arcotangènte
arcotangente arcotangènte s. m. [comp. di arco e tangente]. – In trigonometria, a. di x, l’arco (angolo) la cui tangente trigonometrica è x; simbolo: arctan x.
arctan
arctan (meno bene arctag o arctg). – In matematica, simbolo dell’arcotangente.