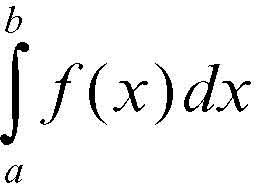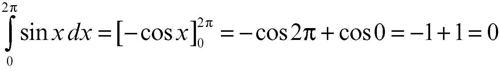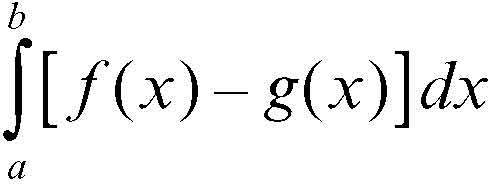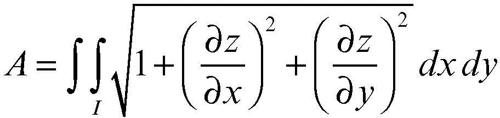area

area

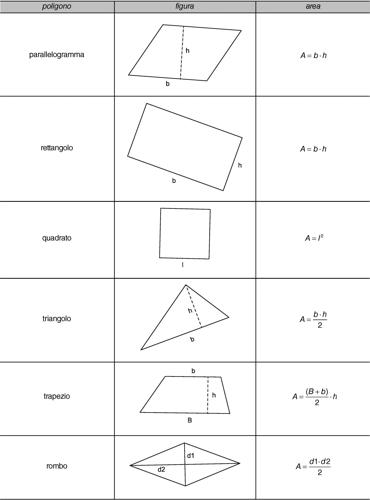
area in geometria, è la misura dell’estensione di una superficie espressa da un numero reale non negativo. Più precisamente, l’area di una superficie è il rapporto tra una regione bidimensionale dello spazio (la superficie stessa) e una superficie piana di riferimento, assunta come unità di misura. Nel SI l’unità di misura della superficie è il metro quadrato (m² o mq), cioè un quadrato di lato 1 m. Altre unità di misura utilizzate sono i suoi multipli o sottomultipli: l’ettaro (ha), usato soprattutto per appezzamenti agricoli ed equivalente a 10.000 m² (area di un quadrato di lato pari a 100 m); il chilometro quadrato (km² o kmq), corrispondente a un milione di m²; il centimetro quadrato (cm² o cmq): 10.000 cm² equivalgono a 1 m². Per calcolare le aree dei poligoni elementari si ricorre alle formule riportate nella tavola. L’area di un poligono qualunque può essere determinata scomponendo il poligono stesso in più triangoli (→ triangolazione) e sommando le aree dei singoli triangoli. Per i triangoli esistono formule specifiche che ne forniscono l’area in funzione dei lati o di due lati e un angolo (→ triangolo).

Area di una superficie piana a contorno curvilineo

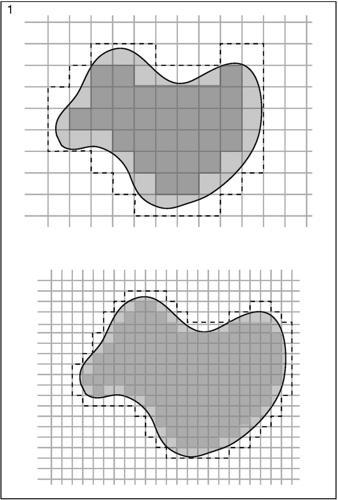
L’area di un cerchio di raggio r è πr²; l’area di un’ellisse di diametri a e b è πab. Per una generica figura piana connessa delimitata da linee curve o miste, curve e rettilinee, l'area può essere determinata attraverso procedimenti di approssimazione. Per esempio, data una figura F, la si può considerare inserita in una quadrettatura del piano (determinata da una data unità di misura).

Si individuano allora due linee spezzate formate con i segmenti della quadrettatura, l’una tutta interna a F l’altra tutta esterna. Tali linee costituiscono il contorno di due poligoni (non necessariamente convessi) l’uno interno e l’altro esterno alla superficie considerata. L’area di F è compresa tra l’area a₁ della figura poligonale inscritta e l’area A₁ della figura poligonale circoscritta. Infittendo la quadrettatura, per esempio dimezzandone il lato, si ottengono altri due poligoni, l’uno inscritto, di, area a₂, l’altro circoscritto, di area A₂. Ripetendo più volte tale procedura (dimezzando cioè ogni volta il lato della quadrettatura) e calcolando ogni volta le aree a_i dei poligoni inscritti e quelle A_i dei poligoni circoscritti, si ottengono due successioni, la prima delle quali è non decrescente (perché è sempre a_i+1 ≥ a_i) e la seconda non crescente (perché A_i+1 ≤ A_i). Le due successioni, che rappresentano rispettivamente approssimazioni per difetto e per eccesso dell’area di F, sono convergenti e la loro differenza A_n − a_n può essere resa piccola a piacere. Il loro elemento di separazione è l’area della figura cercata.

Area di una superficie sottesa al grafico di una funzione

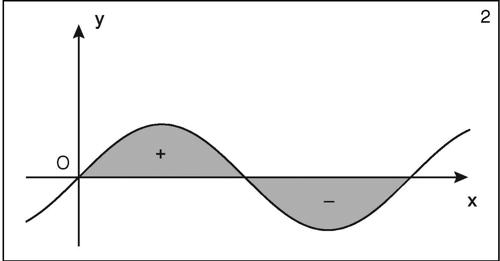
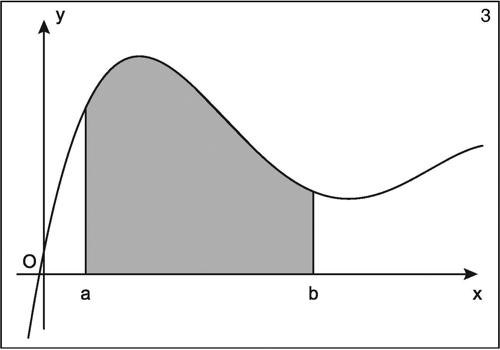
Se y = ƒ(x) è una funzione continua in un intervallo chiuso e limitato [a, b] e in questo intervallo mai negativa, l’area della superficie delimitata dal grafico della funzione stessa, dall’asse delle ascisse e dalle rette di equazioni x = a e x = b, detta anche superficie sottesa al grafico (in grigio nella figura), è

(si legge: «integrale da a a b di ƒ di x in dx»).

Se la funzione, in un intervallo, è continua e negativa, in tale intervallo l’integrale fornisce un valore negativo (detto anche → area con segno) e quindi l’area, in senso proprio, è data dal valore assoluto di tale integrale. Per esempio, data la funzione seno, si ha

perché l’area con segno positivo da 0 a π si somma con l’area di segno negativo e di valore opposto da π a 2π.

Area di una superficie tra due grafici

Se y = ƒ(x) e y = g(x) sono funzioni entrambi continue in un intervallo chiuso e limitato [a, b] e in esso è sempre ƒ(x) ≥ g(x), allora l’area della superficie racchiusa dai grafici delle due funzioni e dalle rette di equazioni x = a e x = b è data da

Se nell’intervallo non è sempre ƒ(x) ≥ g(x) (e quindi i due grafici si intersecano), occorre calcolare separatamente le aree delle diverse regioni individuate dai due grafici in quanto l’integrale definito restituisce non l’area, ma l’area con segno di una superficie.

Area di una superficie nello spazio tridimensionale

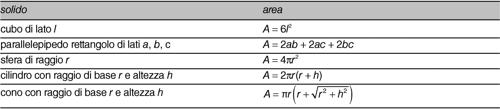
Per i solidi più elementari le formule per il calcolo delle superfici sono riportate in tabella.

Per l’area della superficie laterale di un solido di rotazione si veda la voce → solido di rotazione.

Se la superficie è esprimibile come funzione di due variabili z = ƒ(x, y) differenziabile rispetto alle due variabili nel dominio base I, la sua area è:

essendo

le derivate parziali della funzione, rispettivamente, rispetto a x e y. Se la superficie è espressa attraverso equazioni parametriche x = ƒ₁(u, v), y = ƒ₂(u, v), z = ƒ₃ (u, v), la sua area è:

in cui ƒ_u × ƒ_v indica il prodotto vettoriale delle derivate parziali ƒ_i (con i = 1, 2, 3) rispetto a u e v.