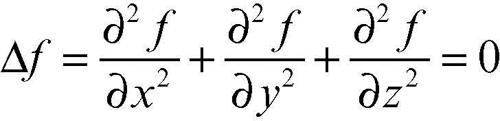armonico

armonico

armonico campo vettoriale che gode contemporaneamente delle proprietà dei campi conservativi e dei campi solenoidali; queste proprietà si esprimono annullando i due operatori rotore e divergenza del vettore v che genera il campo:

La prima relazione afferma la condizione di esistenza di una funzione potenziale ƒ espressa da v = gradƒ. La seconda si può scrivere

dove Δ è il → laplaciano; questa relazione rappresenta un’equazione differenziale (costituita dalle derivate seconde del potenziale rispetto alle tre direzioni degli assi coordinati x, y, z) ed è chiamata equazione di → Laplace:

Ogni campo armonico è caratterizzato da una funzione ƒ, soluzione dell’equazione di Laplace, detta funzione armonica. L’equazione di Laplace riveste grande importanza, in quanto interviene per esempio nella teoria della gravitazione, nei moti irrotazionali dei fluidi, nell’elettrostatica e nella magnetostatica.