asintoto

asintoto

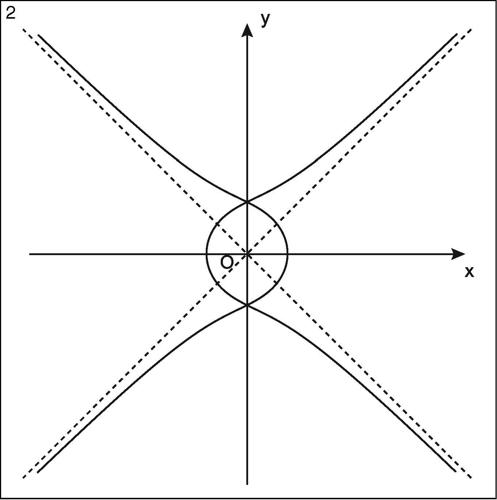
asintoto nella geometria affine, retta tangente a una curva piana in un suo punto all’infinito. Intuitivamente si può dire che la distanza tra essa e il punto della curva tende a zero quando il punto stesso tende all’infinito. Si può, quindi, pensare a un asintoto come alla posizione limite assunta dalla tangente alla curva in un punto al tendere del punto stesso all’infinito (ovvero la retta si avvicina indefinitamente alla curva data). Per determinare gli asintoti di una curva algebrica di grado n si interseca la curva con una retta generica e si impone che l’equazione ottenuta abbia grado minore o uguale a n − 2. Per esempio, la curva di equazione x⁴ − y⁴ + x² + 2y² − 1 = 0 ammette gli asintoti di equazioni y = ±x.

In analisi, generalizzando, si dice che una retta r è un asintoto per una linea L se la distanza di un punto P di L da r tende a 0 quando P tende all’infinito. Se la linea L è il grafico di una funzione di equazione y = ƒ(x), si hanno tre tipi di asintoto dipendenti dalla disposizione di r rispetto agli assi cartesiani:

• un asintoto verticale è una retta di equazione x = h tale che

• un asintoto orizzontale è una retta di equazione y = k tale che

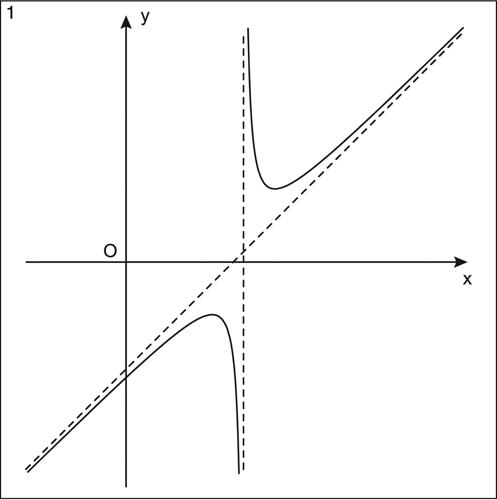
• un asintoto obliquo è una retta di equazione y = mx + q tale che

dove il valore di m è dato da

qualora tale limite esista, sia finito e non nullo.

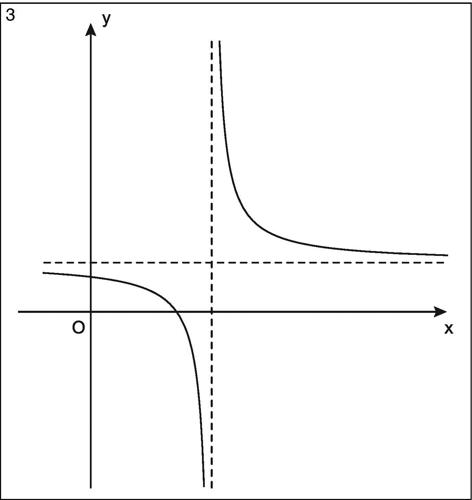
L’asintoto può essere bilatero o unilatero (destro o sinistro) a seconda che vi siano due rami della curva che si accostano alla retta, o uno solo: per esempio l’iperbole di equazione y = 1/x ammette gli assi cartesiani come asintoti bilateri, mentre la linea di equazione y = e^1/x ammette l’asse y come asintoto unilatero destro.

La nozione può essere generalizzata a curve generiche: per esempio si parla di asintoto parabolico per y = ƒ(x) quando esiste una parabola di equazione y = ax² + bx + c tale che