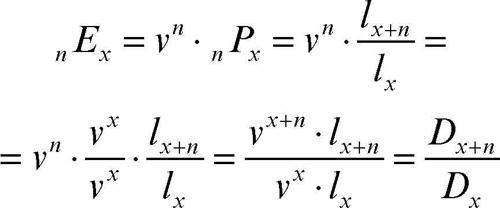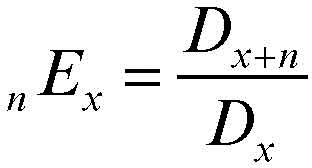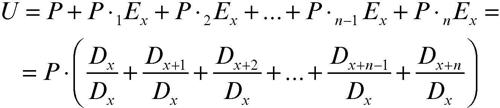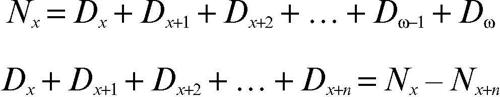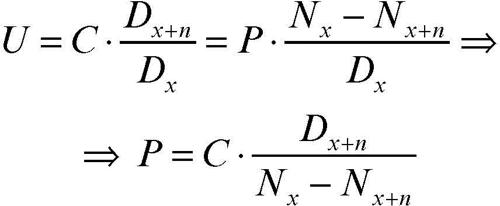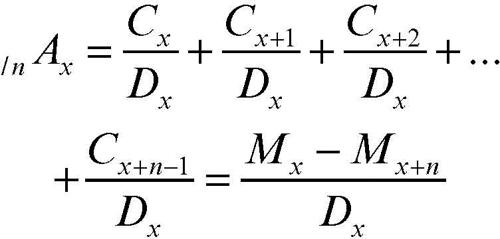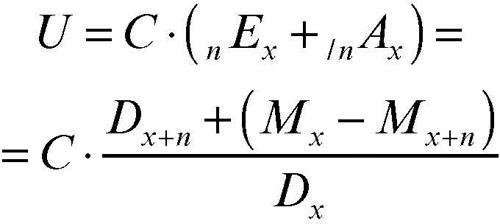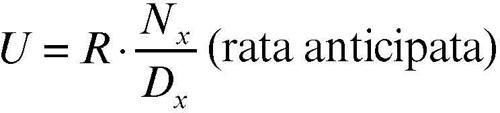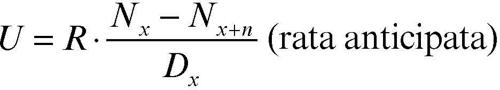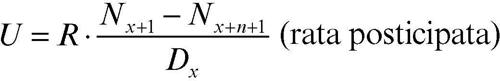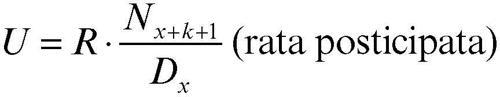assicurazione

assicurazione

assicurazione contratto stipulato tra un soggetto societario assicuratore e persone fisiche o giuridiche, che, a copertura del contratto, pagano un premio unico o periodico. Con la stipula del contratto di assicurazione, l’assicuratore si impegna a pagare, entro i limiti convenuti, il valore dei danni prodotti da un sinistro, oppure un capitale o una rendita al verificarsi di un evento relativo alla morte di una persona o al raggiungimento di un’età prefissata. A seconda dell’oggetto, le assicurazioni sono classificate in assicurazioni contro i danni e assicurazioni sulla vita. In un contratto di assicurazione sulla vita, si distinguono quattro soggetti, alcuni dei quali possono essere una stessa persona o società:

• assicuratore, cioè la società che assume su di sé l’onere di rifondere i danni causati da un sinistro o di pagare la somma convenuta in caso si verifichi l’evento di vita o di morte assicurato;

• contraente, cioè la persona o società che si impegna a pagare il corrispettivo dovuto all’assicuratore ovvero il premio, in unica soluzione oppure in forma rateizzata;

• assicurato, cioè la persona alla quale sono riferiti gli eventi di vita o di morte oggetto del contratto;

• beneficiario, cioè il destinatario delle somme eventualmente pagate al verificarsi degli eventi assicurati.

Il calcolo del premio relativo a un’assicurazione in caso di vita si basa sul principio di composizione dei contratti: se un contratto può essere individuato come composto da più contratti elementari, allora il premio da pagare è la somma dei premi relativi a ogni singolo contratto.

Il valore del premio unico puro per ogni assicurazione elementare si ricava risolvendo l’equazione che nasce uguagliando tra loro la → speranza matematica di ognuno dei due soggetti «in gioco»: assicuratore e contraente. Nello sviluppo dei calcoli si fa riferimento a un premio puro e non anche a somme accessorie, che normalmente vengono stabilite in modo personale o personalizzato dalle compagnie assicuratrici.

Per calcolare il premio unico puro U per un’assicurazione si osserva in generale che:

• la speranza matematica dell’assicuratore è uguale a U, poiché ha la certezza di incassare la somma relativa al premio;

• la speranza matematica del contraente è uguale al valore attuale del capitale C assicurato moltiplicato per la probabilità di sopravvivere dall’età x all’età x + n dell’assicurato (→ funzione biometrica).

L’assicurazione di capitale differito è un’assicurazione elementare per il caso di vita ed è quella per cui, a fronte del pagamento di un premio, un contraente di età x assicura a sé stesso un capitale C al raggiungimento dell’età x + n; in caso di morte prima di tale età, l’assicuratore è libero da ogni obbligo futuro. Il premio unico puro per un’assicurazione di capitale differito è:

In questa formula la variabile v rappresenta il fattore di → sconto e la scrittura _nP_x indica la probabilità che una persona di età x possa sopravvivere fino all’età x + n. Per C = 1, cioè per un capitale assicurato di un solo euro, il premio da pagare è di solito indicato con la scrittura _nE_x, che si legge «E di x differito n», la cui espressione analitica è

Il simbolo l_x+n indica il numero dei sopravvissuti dall’età x all’età x + n.

Nella tradizione della matematica attuariale si è soliti utilizzare particolari simboli, detti simboli di → commutazione. Così, per un’assicurazione di capitale differito, il premio unico puro può essere riscritto nel seguente modo:

Nella formula si è posto D_x = v^xl_x i cui valori sono tabulati in apposite tavole, con riferimento a uno o più tassi d’interesse prefissati. Così, utilizzando i simboli di commutazione _nE_x, D_x+n, D_x, il premio unico puro relativo al capitale di 1 euro è dato da

Per un’assicurazione di capitale differito a premio periodico, il calcolo della rata di premio avviene in base alla considerazione che l’insieme dei premi che deve essere periodicamente versato costituisce per l’assicuratore una rendita attuariale, che l’assicuratore percepirà fino alla scadenza del contratto, salvo morte prematura dell’assicurato.

Ogni singola rata P deve quindi essere considerata come scontata attuarialmente e si ha:

La somma di valori consecutivi del simbolo di commutazione D è parimenti tabulata in tavole attuariali. Si ha:

Con la lettera ⍵ si indica l’età estrema (teorica) di sopravvivenza di un individuo.

Uguagliando le espressioni che indicano il valore attuale attuariale della successione dei premi periodici e il valore del premio unico puro, anticipato, per un’assicurazione di capitale differito, si ottiene la relazione tra premio periodico P da pagare e capitale C assicurato

Un’assicurazione elementare di morte è un’assicurazione per cui, a fronte del pagamento di un premio, il beneficiario ha diritto a riscuotere una determinata somma soltanto se la morte dell’assicurato avviene nel periodo dall’età x + n all’età x + n + 1. La somma assicurata risulta disponibile alla fine del periodo x + n + 1. Considerando che l’assicuratore incassa il premio con certezza, per questo tipo di assicurazione e per il capitale di un euro, il valore del premio unico puro è

Il simbolo _n/1A_x si legge «A di x, differito n e temporaneo 1» e rappresenta il premio unico puro per un’assicurazione elementare di morte relativa a un euro di capitale, a una persona di età x e al fatto che la morte dell’assicurato avvenga nel periodo compreso tra l’età x + n e l’età x + n + 1. Il simbolo d_x+n rappresenta il numero degli individui di età x che non raggiungono l’età x + n.

Un’assicurazione temporanea di morte prevede la copertura del rischio di morire in un determinato periodo di tempo, per esempio dal momento della stipula del contratto e fino al raggiungimento di una determinata età. Il premio unico puro viene calcolato utilizzando il principio di composizione dei contratti.

Il premio unico puro per questo tipo di assicurazione è la somma di tanti premi unici puri relativi a n assicurazioni elementari di morte. Per un capitale assicurato di un euro si ha quindi:

Si definiscono i due seguenti nuovi simboli di commutazione, i cui valori sono riportati in apposite tavole attuariali:

Utilizzando questi simboli di commutazione, l’espressione del premio unico puro diventa

Un’assicurazione mista copre il rischio di morte, per esempio per tutto il periodo contrattuale, e prevede il pagamento di un capitale al raggiungimento di una prefissata età. Tale tipo di assicurazione deriva quindi dall’unione di un’assicurazione temporanea di morte e di un’assicurazione di capitale differito, e si ha la seguente espressione per il premio unico puro:

Al posto di un capitale unico, l’assicurato può decidere per il beneficiario il pagamento di una rendita, temporanea o a vita, cioè fino alla sua morte. Il capitale assicurato C deve quindi essere pensato come il valore attuale attuariale di una rendita. Si hanno perciò le seguenti relazioni per il calcolo del premio unico puro U:

• assicurazione di rendita vitalizia, cioè di rendita periodica fino alla morte del beneficiario:

• assicurazione di rendita temporanea anticipata, cioè di rendita periodica per un numero prefissato n di periodi:

• assicurazione di rendita differita vitalizia anticipata, cioè di rendita che viene corrisposta periodicamente dopo k periodi dal verificarsi dell’evento e fino alla morte del beneficiario:

• assicurazione di rendita differita temporanea anticipata, ovvero di rendita che viene corrisposta periodicamente dopo k periodi dal verificarsi dell’evento e per un numero limitato n di periodi:

Utilizzando il principio di composizione dei contratti si possono derivare le formule per il calcolo del premio, unico o periodico, per qualsiasi tipo di assicurazione.