parallela, assioma della

parallela, assioma della

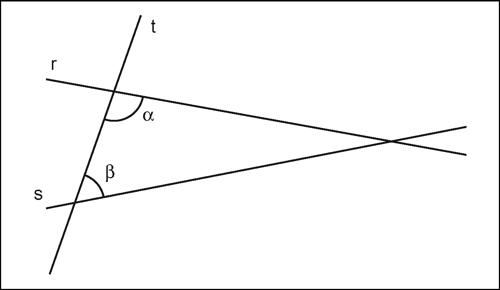
parallela, assioma della assioma della geometria euclidea del piano che, nella sua formulazione corrente, afferma che per ogni retta r e per ogni punto P del piano esiste una sola retta s passante per P e parallela a r. Se P appartiene a r la parallela s coincide con r, in caso contrario è distinta da r e le due rette non si intersecano. Questo enunciato è del tutto equivalente a quello formulato da Euclide nel primo libro degli Elementi. L’enunciato di Euclide, che egli classifica come quinto postulato, stabilisce che se una retta t intersecando due rette r e s forma con esse angoli interni, da una stessa parte, minori di due retti, le due rette, indefinitamente prolungate, si incontrano da quella parte. Tale affermazione appare così evidente da un punto di vista fisico e percettivo che per molti secoli si è pensato che potesse essere dimostrata, cioè che invece di un postulato potesse costituire un teorema, dimostrabile a partire dai primi quattro postulati euclidei. Per secoli i matematici si sono inutilmente adoperati nel tentativo di dimostrare il quinto postulato a partire dai primi quattro. Solo nella prima metà del xix secolo la questione fu definitivamente chiusa quando si dimostrò l’indipendenza del quinto postulato dai primi quattro. Oltre alle geometrie in cui è ammesso tale assioma, esistono così anche geometrie in cui tale assioma è negato o nel senso che non esistono parallele o nel senso che per un punto P esistono più parallele a una retta data (→ geometria non euclidea).