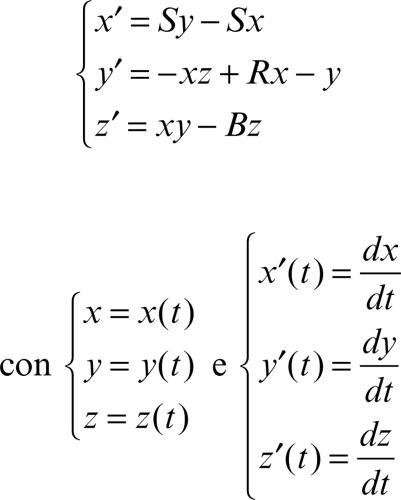Lorenz, attrattore di

Lorenz, attrattore di

Lorenz, attrattore di particolare forma di traiettoria soluzione delle equazioni di Lorenz, costituite dal seguente sistema di equazioni differenziali non lineari:

Le equazioni prendono il nome dal meteorologo e matematico statunitense E.N. Lorenz, che nel 1963 pubblicò un articolo sui modelli non lineari applicati ai moti convettivi presenti nell’atmosfera; le variabili x, y e z forniscono le modalità di movimento del fluido in presenza dei parametri caratteristici S, R, B (dipendenti dalle caratteristiche fisiche del fluido stesso quali la temperatura, la viscosità, la densità) e determinano l’evoluzione temporale del sistema. La forma della soluzione è molto particolare e dipende dai valori di S, R e B. L’attrattore di Lorenz è anche detto attrattore strano di Lorenz, perché, cambiando le condizioni iniziali sui parametri, cambia solo la forma e l’estensione dell’attrattore, ma la traiettoria risultante rimane comunque sempre all’interno della figura. Si dimostra che, partendo da piccole perturbazioni delle condizioni iniziali, le corrispondenti traiettorie si allontanano velocemente, per poi avvicinarsi di nuovo, riallontanarsi ancora una volta e così via. Riferito alla meteorologia, Lorenz dedusse che ciò implicava che piccolissime variazioni delle condizioni iniziali inducevano comportamenti simili solo per brevi periodi iniziali ma comportamenti molto differenti per il lungo periodo. Lo studio di Lorenz fa parte del più complesso problema riguardante la stabilità dei sistemi caotici (→ caos).