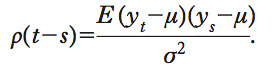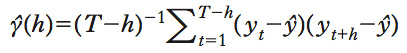autocovarianza

autocovarianza

Covarianza tra elementi di una serie storica in diversi istanti di tempo. L’a. è quindi una misura del grado di dipendenza o memoria delle variabili che compongono una serie storica. Nel caso di una serie storica stazionaria {y_t} a media μ e varianza σ², l’a. tra y_t e y_s dipende solo dalla loro distanza ∣t−s∣ e si scrive (per t≥s) y_t−s= E(y_t−μ) (y_s−μ). In particolare, y₀=σ² coincide con la varianza del processo. L’a., vista come funzione della distanza ∣t−s∣, è detta funzione di autocovarianza. Dividendo per la varianza del processo, si ottiene la funzione di autocorrelazione che, sempre nel caso di una serie storica stazionaria, si scrive

Dalla disuguaglianza di Cauchy-Shwartz, risulta che y_h≤σ², il che implica ρ(h)²≤1. Come la correlazione, l’autocorrelazione è una misura assoluta, indipendente dalla scala delle variabili y_t che compongono il processo. Un’autocorrelazione uguale a più o meno 1 equivale a una perfetta relazione lineare tra y_t e y_s, positiva o negativa, vale a dire che esistono due costanti a e b per cui y_t=a+by_s. Se invece ρ(∣s−t∣)=0, vuol dire che le due variabili y_t e y_s sono incorrelate. Data una serie storica di lunghezza T, stazionaria in media e varianza, y₁, ..., y_t, è possibile stimare in maniera consistente la funzione di a. tramite lo stimatore

dove ŷ è la media campionaria della serie storica. In un modello di regressione con serie storiche la presenza di autocorrelazione negli errori è un problema che può portare a una perdita di efficienza nella stima dei minimi quadrati e a una stima non corretta della varianza delle stime dei coefficienti di regressione. Un possibile test per la verifica della presenza di autocorrelazione negli errori è il test di Durbin-Watson (➔).