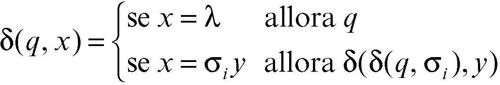automa

automa

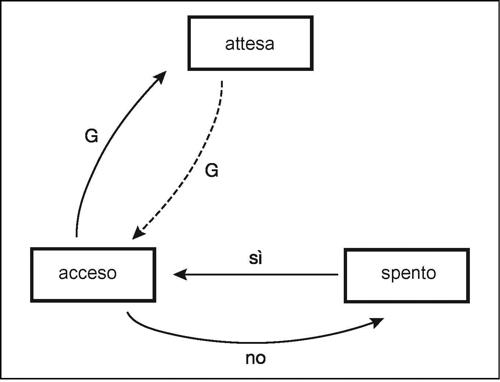
automa dispositivo in grado di effettuare una particolare azione in risposta a stimoli esterni. I computer sono esempi di automi complessi che, a partire da dati e programmi, eseguono i comandi. Un automa può essere studiato sia da un punto di vista tecnico, analizzando i suoi componenti materiali, meccanici o elettronici, sia da un punto di vista matematico, analizzando la logica del suo comportamento. A tale scopo si schematizza un automa mediante gli stati di memoria; un automa si trova in uno o in un altro stato a seconda di ciò che si è verificato precedentemente. Ogni azione compiuta da un automa dipende dallo stato in cui si trova e dalle istruzioni che riceve e che determinano gli eventuali cambiamenti di stato. Per ricevere istruzioni ed effettuare operazioni, è necessario stabilire l’alfabeto dei caratteri (input o output) che esso è in grado di ricevere e di produrre. Un automa è rappresentabile mediante il grafo degli stati i cui nodi rappresentano appunto gli stati mentre gli archi indicano le possibili transizioni da uno stato a un altro. Per esempio, un automa che distribuisce una bibita dopo l’inserimento di due gettoni e che sia munito di una spia che indica la possibilità di inserire la moneta, è caratterizzato da tre stati: «acceso», «spento», «in attesa» del secondo gettone. Gli input possibili, che determinano un eventuale cambiamento di stato, sono tre: 1) G: inserimento di un gettone; 2) l’indicazione «sì» (ci sono bibite disponibili); 3) l’indicazione «no» (non ci sono bibite disponibili).

«Sì» e «no» sono input perché sono indicazioni che l’automa riceve da un organo di controllo e in base alle quali opera. L’output è rappresentato dall’erogazione della bottiglia e, nel grafo in figura, è rappresentato da una freccia tratteggiata.

Il comportamento dell’automa può essere anche rappresentato dalla seguente matrice di transizione:

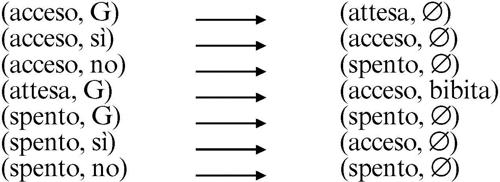
In corrispondenza della casella in grigio l’automa eroga la bibita. Le due caselle vuote indicano che nello stato di attesa l’informazione circa la presenza o meno di bibite è ininfluente. Il comportamento dell’automa può ulteriormente essere rappresentato con un insieme di istruzioni che a una data coppia (stato, input), detta anche configurazione, fanno corrispondere univocamente una configurazione (stato, output) in cui l’output può anche essere vuoto (∅) cioè non esistere:

Un automa come il precedente che esegue un’azione è detto anche automa esecutore. Con lo stesso schema logico, si progettano anche automi che stabiliscano se una stringa di simboli appartiene o meno a un dato insieme: si parla in tali casi di automi riconoscitori di un linguaggio.

Dal punto di vista teorico, gli automi più elementari sono gli automi a stati finiti detti anche automi finiti deterministici: essi hanno un numero finito di stati e operano in modo deterministico (per ogni stato e in corrispondenza di un dato input è determinata la transizione alla successiva configurazione). Formalmente un automa finito deterministico è definito come una quintupla A = (∑, S, F, δ, q₀) dove ∑ = {σ₁, σ₂, ..., σ_n} è un alfabeto,

è un insieme finito di stati, q₀ ∈ S è un particolare stato detto stato iniziale, e F ⊆ S è un particolare insieme di stati detti stati finali. Infine δ: S × ∑ → S è una funzione che a ogni coppia (stato, carattere) associa uno stato e che, avendo dominio finito, può essere rappresentata con una matrice. Si dice funzione di transizione l’estensione S × ∑* → S della funzione δ, avendo indicato con ∑* l’insieme delle stringhe costruite a partire dall’alfabeto ∑. Essa è così definita ricorsivamente (λ indica la stringa vuota nell’insieme ∑*):

Il linguaggio accettato dall’automa A è l’insieme L(A) = {x | δ(q₀, x) ∈ F}. Tale insieme è un sottoinsieme di ∑*, eventualmente coincidente con esso.

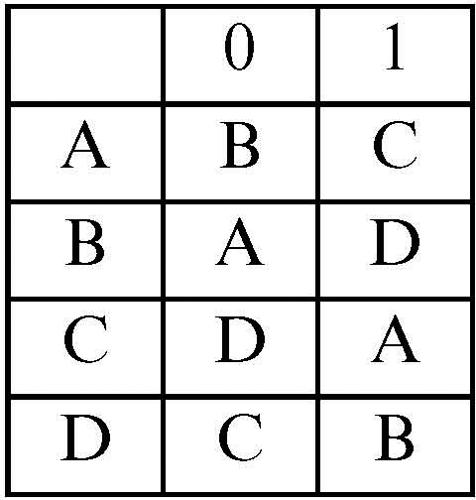
Per esempio, l’automa finito A = (∑, S, δ, q₀, F) dove ∑ = {0, 1}, S = {A, B, C, D}, q₀ = A, F = {A, B, C} e la cui matrice di transizione è la seguente:

accetta tutte le parole che contengono un numero pari di 0 o un numero pari di 1: questo è il linguaggio accettato dall’automa. Un linguaggio accettato (o, equivalentemente, riconosciuto) da un automa finito deterministico è detto linguaggio regolare. È possibile definire anche un automa finito non deterministico come una quintupla A_N = (∑, S, F, δ_N, q₀) dove ∑, S, F, q₀ hanno lo stesso significato che hanno nella definizione di un automa deterministico, mentre la funzione di transizione δ_N associa a ogni coppia (stato, carattere) un sottoinsieme di S, eventualmente vuoto; non associa, quindi, uno stato come nel caso deterministico, bensì un insieme di stati (da qui il non determinismo). Analogamente al caso deterministico si può definire la classe dei linguaggi accettati (riconosciuti) da un automa finito non deterministico. Gli automi finiti deterministici sono un sottoinsieme di quelli non deterministici.

Automi più complessi riconoscono classi di linguaggi più ampie; tuttavia, aumentando la complessità diminuisce la decidibilità dei problemi che si definiscono su essi. Così, mentre i linguaggi regolari sono poco descrittivi, ma è sempre decidibile se essi godano o meno di una determinata proprietà, i linguaggi riconosciuti da automi non deterministici sono maggiormente descrittivi, ma molti problemi che li riguardano non sono decidibili. Si costruisce così una gerarchia di complessità dei vari automi, analoga alla gerarchia di ampiezza dei linguaggi formali (→ Turing, macchina di).