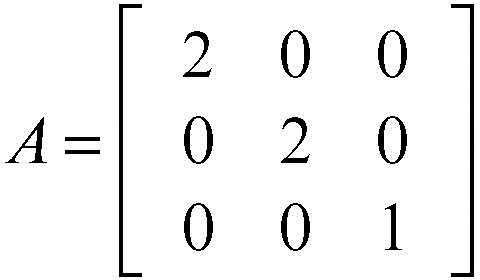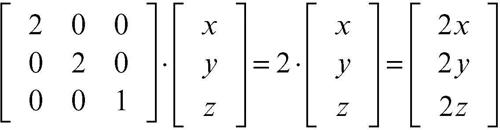autospazio

Enciclopedia della Matematica (2013)

autospazio


autospazio sottospazio di uno spazio vettoriale V formato dal vettore nullo e da tutti gli autovettori associati a un determinato autovalore. Per esempio in R3, spazio vettoriale di dimensione 3 sui reali, la trasformazione definita dalla matrice

formula

ha per polinomio caratteristico p(λ) = (2 − λ)2(1 − λ) le cui radici (autovalori) sono λ1 = 2, con molteplicità 2, e λ2 = 1. Gli autovettori corrispondenti all’autovalore λ1 sono tutti e soli i vettori v = [x y z] di R3 tali che A · v = 2 · v cioè tali che

formula

e che quindi sono esprimibili nella forma [u t 0] con u, t ∈ R. Posti u = 1, t = 0 e u = 0, t = 1 si ottengono, rispettivamente, gli autovettori v1 = [1 0 0] e v2 = [0 1 0] che generano un sottospazio di dimensione 2 (il piano di equazione z = 0). Tutte le direzioni che giacciono sul piano z = 0 restano invariate nella trasformazione affine definita dalla matrice A.

Vedi anche
matrice Anatomia Ammasso di cellule epiteliali alla cui attività si deve la formazione di un tessuto. M. dell’unghia L’ammasso di cellule dello strato onicogeno che si osserva in corrispondenza della radice dell’unghia e della lunula, e alla cui opacità è dovuto il colorito biancastro di quest’ultima. M. del ... determinante Biologia Termine introdotto da A. Weismann per indicare presunti aggregati di molecole contenuti nel nucleo delle cellule sessuali e che conterrebbero i fattori per la determinazione delle cellule. In immunologia, d. antigenico, sito dell’antigene contro cui è diretta la specificità di un anticorpo; ... ortogonale In geometria elementare si dice di due enti che formano tra loro un angolo retto. fig. 1 ADue rette r, s del piano si dicono o. (o perpendicolari) se si intersecano formando quattro angoli retti (fig. 1 A); una retta r dello spazio si dice o. (o perpendicolare) a un piano α se incontra il piano in ... osservabile In fisica, si dice di grandezza che ha la proprietà dell’osservabilità, è cioè suscettibile di essere misurata. Le variabili dinamiche di un sistema fisico che siano suscettibili di determinazione sperimentale sono chiamate le o. del sistema: ogni teoria che pretenda di descrivere il comportamento del ...
Tag
Altri risultati per autospazio
  • autovettore
    Dizionario di Economia e Finanza (2012)
    Un a. di una matrice (➔) quadrata è un vettore non-nullo che, moltiplicato per la matrice stessa, resta proporzionale al vettore originario, senza cambiare direzione. Per ogni a., il fattore di proporzionalità corrispondente si chiama autovalore. Formalmente, se A è una matrice quadrata, il vettore ...
  • autovettore
    Enciclopedia on line
    In matematica, a. di una trasformazione lineare T è un vettore A la cui direzione non varia per l’applicazione di T: cioè TA=kA, con k grandezza scalare, autovalore (➔) della trasformazione.
  • autovalore
    Enciclopedia della Scienza e della Tecnica (2008)
    Luca Tomassini Tanto in algebra quanto in analisi, si è frequentemente condotti a definire e a calcolare delle funzioni (inverso, potenze, esponenziali ecc.) di un endomorfismo A:V→V di uno spazio vettoriale V sul campo dei numeri complessi ℂ. A questo fine, è utile determinare le rette di V stabili ...
  • autospàzio
    Dizionario delle Scienze Fisiche (1996)
    autospazio autospàzio [Comp. di auto- e spazio] [ALG] Di un operatore lineare A definito su uno spazio vettoriale X, è un sottospazio A⊂X tale che se x∈A, allora Ax∈A; si usa anche dire, se λ è un autovalore di A, che i vettori verificanti Ax=λx appartengono all'a. generato dall'autovalore λ. ◆ [MCC] ...