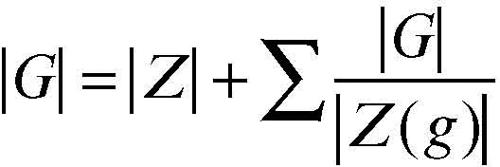azione
azione
azione di un gruppo G su un insieme X è un’applicazione ∗: G × X → X, che soddisfa le seguenti proprietà:
• u ∗ x = x per ogni x appartenente a X (dove u indica l’elemento neutro di G);
• g1 ∗ (g2 ∗ x) = (g1g2) ∗ x per ogni x appartenente a X e ogni g1, g2 appartenenti a G.
Ogni elemento g di G determina dunque una corrispondenza biunivoca ψg di X in sé stesso, data da ψg(x) = g ∗ x e con inversa
Se S(X) indica il gruppo delle permutazioni di X, allora le condizioni imposte equivalgono ad affermare che l’applicazione ψ: G → S(X), che associa a g la permutazione ψg di X, è un omomorfismo di gruppi. Se è data un’azione del gruppo G sull’insieme X, si dice allora che G agisce su X e X è detto un G-spazio. Un importante esempio di azione è l’azione di coniugio di un gruppo su sé stesso, definita da g ∗ h = ghg−1.
Se x è un elemento di un G-spazio X, si chiama orbita di x il sottoinsieme di X, indicato con Gx, definito da Gx = {g ∗ x : g ∈ G}; per esempio, nell’azione di coniugio di un gruppo su sé stesso, le orbite coincidono con le classi di coniugio; in tal caso l’orbita di un elemento g si riduce al solo g se e solo se g è nel centro del gruppo. Date due orbite, esse o coincidono oppure hanno intersezione vuota; la suddivisione in orbite determina dunque una partizione dell’insieme X.
Se x è un elemento di X, si chiama stabilizzatore (o gruppo di isotropia) di x il sottogruppo di G, indicato con Stx, costituito dagli elementi che mantengono fisso x: Stx = {g ∈ G : g ∗ x = x}. Se x e y sono due elementi di X appartenenti alla stessa orbita, supponiamo y = g ∗ x, allora i rispettivi stabilizzatori sono coniugati in G: Stg∗x = g Stx g−1. Per esempio, nel caso dell’azione di coniugio di un gruppo su sé stesso, lo stabilizzatore di un elemento g coincide con il suo centralizzatore Z(g). L’orbita e lo stabilizzatore di un elemento x sono legati dalla relazione |Gx| = [G : Stx], dove |Gx| e [G : Stx] indicano rispettivamente la cardinalità di Gx e l’indice del sottogruppo Stx in G. Se G è un gruppo finito, allora l’equazione si può riscrivere come |Gx| = |G | / |Stx|: la cardinalità dell’orbita di un elemento di X è uguale al rapporto tra la cardinalità di G e quella del suo stabilizzatore. Nel caso dell’azione di un gruppo finito G su sé stesso, se Z ne indica il centro e se Z(g) indica il centralizzatore di un elemento g, allora si ottiene la cosiddetta equazione delle classi
dove la somma è estesa a tutti gli elementi g non appartenenti al centro Z, uno per ogni classe di coniugio.