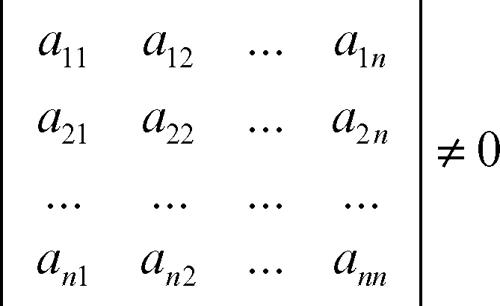spazio, base di uno

spazio, base di uno

spazio, base di uno insieme di elementi di uno spazio attraverso i quali è possibile esprimere tutti gli elementi dello spazio stesso.

☐ In uno → spazio vettoriale, una n-pla di vettori (v₁, ..., v_n) costituisce una sua base se essi:

• risultano linearmente indipendenti;

• generano lo spazio vettoriale, cioè ogni vettore dello spazio è esprimibile come loro combinazione lineare.

Per esempio nello spazio vettoriale R³, una base è costituita dalla terna di vettori e₁ = (1, 0, 0), e₂ = (0, 1, 0), e₃ = (0, 0, 1) (detta base canonica). Più in generale, n vettori v₁ = (a₁₁, ..., a_1n), ..., v_n = (a_n1, ..., a_nn) di uno spazio vettoriale Rⁿ, di dimensione n, formano una base di Rⁿ se e solo se risulta

☐ In uno → spazio topologico X con topologia T una collezione B di aperti di T è detta una base della topologia o base dello spazio topologico se ogni insieme aperto di T è unione (finita o infinita) di elementi di B. Si dice che la base genera la topologia T, i cui aperti si ottengono mediante unione di elementi della base stessa. Due topologie con la stessa base sono identiche. Una base caratterizza tutte le proprietà topologiche dello spazio. Una base B di uno spazio topologico X verifica le seguenti tre proprietà:

• ∅ ∈ B;

• gli elementi della base ricoprono X;

• l’intersezione di due qualsiasi elementi della base si può ottenere come unione di elementi della base.

☐ In uno → spazio metrico dotato della struttura di spazio topologico una base è data, per esempio, da tutte le sfere aperte aventi centro nei vari punti e raggio assegnato r. Come base minima per definire una topologia in un insieme X si può scegliere quella costituita da ∅ e X (topologia banale).