BIOMATEMATICA
Biomatematica
La b. si occupa dell'applicazione di metodi matematici per descrivere dal punto di vista qualitativo e quantitativo il comportamento di sistemi biologici. A tal fine il compito del biomatematico consiste nell'identificare un sistema di equazioni, chiamato modello matematico, la cui soluzione sia in grado di descrivere il particolare fenomeno di interesse con l'approssimazione desiderata.
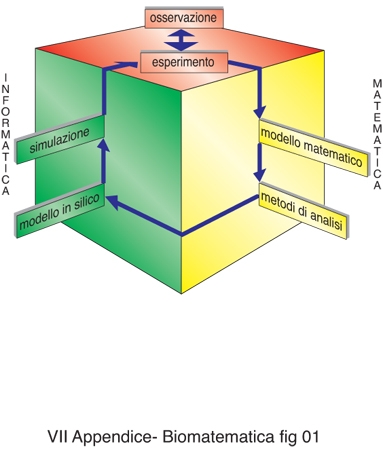
Infatti, come per la maggior parte dei problemi di matematica applicata e industriale, la profonda complessità che caratterizza gli organismi viventi e le innumerevoli relazioni esistenti tra le varie componenti di un sistema biologico, dove tutto sembra interagire con tutto, rendono impossibile descrivere il sistema nella sua interezza. È necessario quindi approssimare la realtà focalizzandosi su fenomeni specifici, introducendo sia modelli biologici sia modelli matematici capaci di descriverli. Va tuttavia tenuto presente che in biologia e in medicina risulta molto complicato ridurre la descrizione fenomenologica a poche variabili significative, come d'altronde è richiesto dalla formalizzazione matematica. Per questo motivo, probabilmente il passo più difficile nella deduzione di un modello biomatematico è proprio il primo, quello che consiste nel passare dalla descrizione dello specifico fenomeno che si vuole studiare all'identificazione delle variabili di stato considerate rappresentative del sistema e delle variabili indipendenti di cui le variabili di stato sono funzione. Per es., i modelli di dinamica delle popolazioni studiano l'evoluzione delle diverse popolazioni, eventualmente differenziandone il sesso, tipicamente in funzione del tempo e dello spazio, ma potrebbe essere necessario introdurre altre variabili indipendenti come l'età, la resistenza a contrarre determinate malattie, o, nel caso di studi di carattere sociale, caratteristiche personali quali la capacità persuasiva, l'influenzabilità o la ricchezza. Riuscendo ad approssimare la realtà e descrivendone sia qualitativamente sia quantitativamente il comportamento e l'evoluzione, un modello biomatematico soddisfacente può contribuire così alla comprensione del fenomeno biologico, permettendone la simulazione numerica al calcolatore (detta anche modello in silico). La simulazione consente, per es., di visualizzare l'evoluzione del sistema, di focalizzare l'attenzione su caratteristiche specifiche, di prevedere il comportamento asintotico del sistema e la sua dipendenza dai parametri e in particolare di prevedere il risultato di alcuni esperimenti non ancora svolti (fig. 1). In questo modo un buon modello matematico può in linea di principio aiutare a ottimizzare la sperimentazione identificando le indagini e le strategie più promettenti, e a ridurre in tal modo i tempi e i costi della ricerca.
Più il fenomeno è ripetibile e schematizzabile usando un numero ridotto di variabili, più è facile pensare all'applicabilità del procedimento appena descritto e alla validazione sperimentale dei risultati ottenuti. Per tale ragione tradizionalmente i modelli matematici sono stati sviluppati più in ambito meccanico e fisico che in ambito biologico. D'altra parte, è difficile immaginare di poter imbrigliare il comportamento di organismi viventi così complessi in leggi ed equazioni. Infatti, H.A. Hartwell e i suoi collaboratori nel 1999 affermarono che "sebbene i sistemi viventi obbediscono alle leggi della fisica e della chimica, il concetto di funzione e finalità differenzia la biologia dalle altre scienze naturali" (H.A. Hartwell, J.J. Hopfield, S. Leibler et al., From molecular to modular cell biology, in Nature, 1999, 402, pp. c47-c52).
Sviluppo della biomatematica
Per i motivi appena menzionati, lo sviluppo della b. è stato frenato in passato da un certo scetticismo da parte dei biologi sulle effettive capacità della matematica di descrivere i sistemi biologici. Ciò ha comportato difficoltà nello sviluppare quelle interazioni interdisciplinari necessarie per lo sviluppo di applicazioni concrete. Nell'ultimo decennio tale scetticismo è andato via via diminuendo e si è avuta un'esplosione di interesse nella biomatematica. Tale fatto è dimostrato dal moltiplicarsi di attività didattiche di tipo interdisciplinare e dallo spostamento dei ricercatori da settori di ricerca tradizionali a settori di ricerca che si interfacciano con la biologia. I motivi di questo cambiamento sono molteplici e l'analisi può essere soggettiva. Alcuni motivi possono essere identificati nel maggiore interesse per tematiche di tipo ambientale, nella nascita di legislazioni specifiche quali la valutazione di impatto ambientale, nella richiesta di oggettivazione delle osservazioni biomediche e nella necessità di ottimizzare procedure e protocolli, per es. legati alla somministrazione di farmaci o alla combinazione ottimale di terapie.
Un momento di svolta si è avuto sicuramente con lo sviluppo e la disponibilità a costi contenuti di mezzi informatici che hanno reso possibile la creazione di un'interfaccia comprensibile tra matematico e biologo. Il risultato del modello matematico quindi non è espresso solo in termini di equazioni o di grafici, a volte difficilmente leggibili da non specialisti, ma è visualizz ato utilizzando una realtà virtuale.
Un altro punto di svolta, forse di riconoscimento meno immediato, è probabilmente rappresentato dalla decodifica del genoma umano, dalla nascita della proteomica e dall'interesse nello studio delle cascate proteiche. Infatti, con l'inizio dell'era postgenomica, medici e biologi si sono trovati ad avere a disposizione una quantità enorme di dati da comprendere e da mettere in ordine e quindi alla necessità di coinvolgere nella loro ricerca, per es., esperti di sistemi complessi, probabilità, statistica, crittografia, meccanica statistica. La necessità di collaborazione ha reso possibile lo sviluppo di interazioni interdisciplinari non estemporanee, ma caratterizzate da una continuità temporale e da una comunione di intenti.
Una volta rotto il ghiaccio e acquistata fiducia nelle potenzialità di una ricerca multidisciplinare l'interazione ha permesso di rispondere anche a un'esigenza di tipo evoluzionistico tipica della ricerca in campo biomedico. Il medico infatti, avendo a disposizione i risultati di esami diagnostici effettuati in un determinato istante dell'evoluzione del fenomeno, o, nei casi più fortunati, di una serie di dati rilevati durante un periodo di osservazione, ha tipicamente tre esigenze: la prima è quella di capire come si è arrivati alla situazione patologica che viene osservata in quel momento, la seconda è quella di comprendere cosa succederà in futuro, la terza è quella di dedurre se e come intervenire ottimizzando il tipo di intervento. Dal punto di vista matematico il primo è un problema inverso perché dalla situazione presente si vogliono ricavare informazioni nel passato, il secondo è un problema diretto perché si vuole prevedere l'evoluzione futura e il terzo è un problema di ottimizzazione e di controllo.
Biomatematica e medicina
Il mondo biomedico non è estraneo al concetto di modello, anche se per medici e biologi modello è sinonimo di esperimento, sia esso in vitro, ex vivo o in vivo. Infatti anche nella ricerca medica è necessario effettuare, partendo dall'esperienza clinica, passi sequenziali di astrazione e semplificazione allo scopo di comprendere singolarmente gli aspetti che costituiscono i complessi fenomeni che avvengono in natura. La b. si sta inserendo nel processo di modellizzazione aggiungendo un anello matematico che rappresenti virtualmente il fenomeno biomedico di interesse (fig. 2).
Riassumendo, dall'osservazione fenomenologica di un certo fenomeno sul paziente, i ricercatori in biomedicina cercano di sviluppare modelli biologici, in vivo (per es., su cavie o embrioni di pollo) e in vitro, che risultino più maneggevoli, riproducibili e relativamente inoffensivi. I biomatematici, a questo punto, cercano di generare modelli matematici a partire sia dall'osservazione fenomenologica diretta sia dal modello biologico. L'acquisizione di tale conoscenza è, quindi, sottoposta a test utilizzando varie fasi sperimentali caratterizzate da una crescente complessità per essere applicata alla pratica clinica. È chiaro che questo processo presenta anche un problema etico, perché coinvolge progressivamente esperimenti su piccoli mammiferi, grandi mammiferi, su malati terminali e non, secondo diverse fasi di sperimentazione strettamente controllate; l'uso dei modelli potrebbe aiutare a ridurre il numero di esperimenti su animali e quindi il costo e i tempi necessari per la fase sperimentale. Per questi motivi, in diversi centri ospedalieri, soprattutto statunitensi, incominciano a essere presenti ricercatori con conoscenze fisico-matematiche-informatiche utilizzati come supporto per la determinazione di protocolli e per la visualizzazione diagnostica. I campi di applicazione della b. sono molteplici e si sono andati moltiplicando. La fiducia nelle potenzialità della b. è cresciuta tanto da far ritenere che la matematica potrebbe svolgere nel 21° sec. per la biologia e la medicina quel fondamentale ruolo di supporto svolto per la meccanica nel 19° sec. e per la fisica nel 20° secolo. Tra la fine del 20° sec. e gli inizi del 21° si è registrato uno spostamento di attenzione da applicazioni tradizionali quali l'ecologia, la dinamica delle popolazioni e l'epidemiologia a nuovi settori: la bioinformatica, la biostatistica, la genomica, la proteomica e la medicina.
Anche nel campo dell'epidemiologia, l'attenzione è stata dedicata soprattutto allo studio della diffusione di nuove o pericolose malattie quali l'AIDS o la SARS (Severe Acute Respiratory Syndrome). Quando sono scoppiate le emergenze legate alla loro diffusione, sono stati subito applicati metodi tradizionali della b. per cercare di prevedere l'evolversi delle epidemie. Modelli matematici di epidemiologia e dinamica delle popolazioni erano stati sviluppati per casi relativamente più semplici già da G. Bernoulli (intorno al 1760) e V. Volterra (intorno al 1930). Nel caso dell'AIDS, per es., è stato necessario considerare che il meccanismo di contagio è di tipo sessuale o per scambio di sangue infetto, coinvolgendo comunità particolari, quali i tossicodipendenti, o legami genitoriali diretti, quali madre-figlio. Quindi i modelli matematici hanno dovuto considerare variabili quali il sesso, l'età, le abitudini sessuali, gli stili di vita, i ritardi tra il contagio e la conclamazione della malattia. Le stesse tecniche sono state applicate anche ad applicazioni insolite come il matrimonio e dopo gli eventi dell'11 settembre 2001 alla valutazione degli effetti del bioterrorismo. Le applicazioni alla medicina riguardano soprattutto le malattie più diffuse o letali, come le malattie del sistema nervoso, del sistema circolatorio e la nascita e la diffusione di tumori. In Europa e in Italia gli ultimi due ambiti si sono sviluppati in modo particolare grazie al finanziamento di due progetti di ricerca multinazionale coordinati rispettivamente dai Politecnici di Milano e di Torino. Approfittando di questa possibilità molti ricercatori hanno indirizzato le loro conoscenze di meccanica dei continui, fluidodinamica numerica, sistemi complessi e teorie cinetiche verso lo studio di problematiche biomediche. Considerando il sistema circolatorio, si è cercato di descrivere il moto del sangue nelle grandi arterie (per es., l'aorta) o nelle biforcazioni (per es., la biforcazione carotidea), la formazione di placche e di aneurismi, l'accoppiamento tra grande e piccola circolazione, l'ossigenazione del sangue, il flusso nelle reti di capillari, la perfusione di fluido e nutrienti attraverso la parete dei capillari, il trasporto e la diffusione di farmaci nel sistema circolatorio e nei tessuti, la reologia del sangue, l'accoppiamento tra flusso sanguigno e deformazione delle pareti dei vasi, la forma dei globuli rossi, la formazione di nuovi vasi sanguigni e il loro rimodellamento.
Modellazione multiscala
Nell'applicazione della matematica alla medicina è evidente fin dal primo passo del processo di modellazione, ossia la descrizione fenomenologica, che lo studio dei fenomeni coinvolti dipende dalla lente di ingrandimento, reale o ideale, utilizzata dal biologo nel descrivere i fenomeni in gioco.
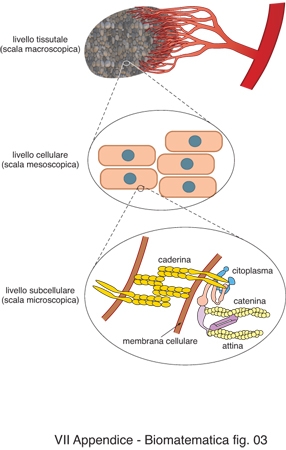
Si può infatti descrivere ciò che accade a livello subcellulare, a livello cellulare o a livello tissutale (fig. 3). Si realizza subito però che ciò che accade ai vari livelli è logicamente e funzionalmente interconnesso, per cui i problemi biomedici sono intrinsecamente multiscala e i modelli matematici da sviluppare dovrebbero essere analoghi. Tale campo di ricerca è in grande sviluppo nella matematica. Infatti, prendendo a titolo di esempio lo sviluppo di tumori, a livello tissutale, corrispondente alla scala macroscopica, sono stati modellati fenomeni quali: la crescita degli sferoidi multicellulari nella fase avascolare, ossia quando la massa tumorale, relativamente piccola (circa 1 mm di diametro) non è ancora circondata da una rete di capillari; la formazione, la degradazione e la rottura di follicoli che a volte circondano la massa tumorale; l'interazione meccanica tra il tumore e i tessuti circostanti; il processo di angiogenesi con cui il tumore stimola la formazione di una rete di capillari per rifornirsi di una maggiore quantità di nutrienti; la crescita vascolare; il distacco di metastasi, il processo di penetrazione nel sistema vascolare (intravasazione e successiva extravasazione) e l'adesione in siti secondari. Si deducono quindi modelli che spesso si scrivono come sistemi di equazioni non lineari alle derivate parziali, a volte caratterizzati dalla presenza di interfacce e frontiere libere, per es. il bordo del tumore o l'interfaccia tra tessuti differenti. Tutti i processi appena menzionati chiaramente dipendono da quanto accade a una scala più piccola, vale a dire a livello cellulare. A questa scala bisogna tener conto che tutte le cellule evolvono, in particolare le cellule tumorali, le quali diventano sempre più aggressive acquisendo capacità e proprietà diverse. Analogamente il sistema immunitario si attiva quando riconosce un aggressore. Dal punto di vista della modellazione ciò comporta la necessità di introdurre tra le variabili indipendenti una nuova quantità che sia capace di descrivere lo stato interno di una popolazione cellulare, in modo da determinare l'evoluzione in termini di una descrizione statistica sullo stato di progressione o attivazione. Inoltre bisogna considerare l'effetto delle interazioni tra le cellule tumorali e le altre cellule del corpo umano, quali le cellule del sistema immunitario, per es. linfociti e macrofagi. I modelli che sono stati sviluppati per trattare fenomeni a questa scala utilizzano spesso automi cellulari, random walk, modelli particellari o si sviluppano nell'ambito delle teorie cinetiche. A sua volta il comportamento intercellulare dipende da quello che succede a una scala ancora più piccola, il livello subcellulare, e quindi dai fenomeni che avvengono all'interno della cellula o alla membrana cellulare, quali meccanismi di degradazione del DNA, espressione genica, alterazione del ciclo cellulare, assorbimento dei nutrienti, produzione e trasduzione di quei segnali che regolano importanti attività cellulari, quali duplicazione, morte, movimento, adesione oppure distacco delle cellule. I modelli microscopici atti a descrivere i fenomeni che avvengono alla scala subcellulare spesso si scrivono come sistemi di equazioni non lineari alle derivate ordinarie, oppure utilizzano metodi statistici, automi cellulari e reti neurali.
Come già ricordato e come messo in evidenza in fig. 3, naturalmente quanto avviene a una certa scala è fortemente legato alle altre scale. Risulta quindi impossibile descrivere l'intero fenomeno senza considerare quello che succede a una scala più piccola o più grande. Dal punto di vista matematico ciò vuol dire che il problema è intrinsecamente multiscala e che l'uso di metodi e modelli matematici multiscala è quanto meno desiderabile, se non necessario. Si sta tentando di collegare i modelli matematici sviluppati su scale diverse, in quanto nella maggior parte dei casi i parametri necessari come input in un modello sono ottenuti dall'output di un altro modello a una scala diversa. Per es., un'alterazione di tipo genetico può determinare la sovraespressione o sottoespressione di una particolare proteina (ossia la presenza di una quantità rispettivamente maggiore o minore di molecole rispetto alla norma). Ogni proteina è coinvolta in diverse reazioni enzimatiche che innescano altre reazioni con un susseguirsi di interazioni, di formazione e rottura di complessi che prendono il nome di cascate proteiche. In questo modo un'alterazione genica influenza l'output della cascata proteica e quindi il comportamento della singola cellula e dell'intero tessuto. Per es., una cellula può diventare insensibile ai segnali di inibizione della crescita trasmessi all'interno della cellula quando questa aderisce ad altre cellule, perché nella cascata proteica che segnala al nucleo la raggiunta confluenza delle cellule si altera qualcosa. La conseguenza è che le cellule continuano a duplicarsi dando luogo a tumori.
bibliografia
J. Keener, J. Sneyd, Mathematical physiology, New York 1998.
F. Brauer, C. Castillo-Chavez, Mathematical models in population biology and epidemiology, New York 2001.
J.M. Gottman, J.D. Murray, C. Swanson et al., The mathematics of marriage: dynamic non linear models, Cambridge (Mass.) 2002.
H.T. Banks, C. Castillo-Chavez, Bioterrorism: mathematical modeling applications in homeland security, Philadelphia 2003.
J.D. Murray, Mathematical biology, 2 voll., New York 2003.
C. Pozrikidis, Modeling and simulation of capsules and biological cells, Boca Raton 2003.
L. Preziosi, Cancer modelling and simulation, Boca Raton 2003.
M. Amos, Cellular computing, Oxford-New York 2004.
N.F. Britton, Essential mathematical biology, London 2005.
M. Iannelli, M. Martcheva, F.A. Milner, Gender-structured population modeling: mathematical methods, numerics and simulations, Philadelphia 2005.