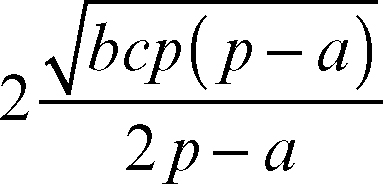bisettrice
bisettrice
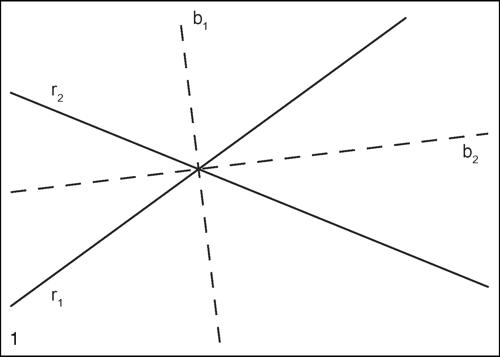
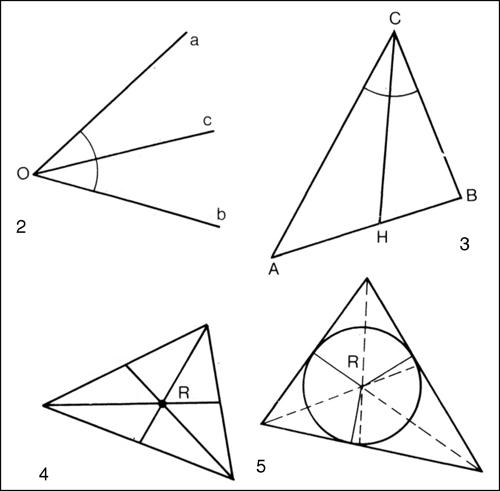
bisettrice nel piano, la bisettrice di un angolo è la retta passante per il vertice che divide l’angolo in due angoli di uguale ampiezza. Ha la proprietà di essere il luogo dei punti equidistanti dalle rette alle quali appartengono i lati dell’angolo. Due angoli opposti al vertice hanno per bisettrici la stessa retta. Le bisettrici dei quattro angoli formati da due rette incidenti risultano tra loro perpendicolari. Per la costruzione della bisettrice di un angolo si veda → angolo, bisezione di un.
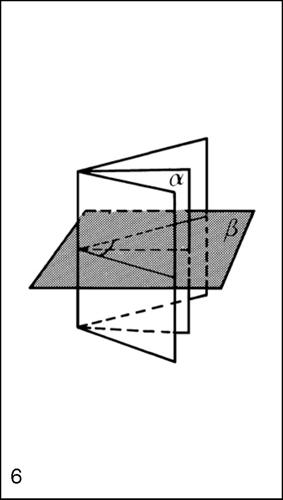
Nello spazio tridimensionale la bisettrice di un diedro (detta anche bisettore) è il piano passante per lo spigolo che divide il diedro in due diedri di uguale ampiezza. La bisettrice di un diedro ha la proprietà di essere il luogo dei punti equidistanti dai piani ai quali appartengono le facce del diedro. In un triangolo, la bisettrice di ogni suo angolo interno divide il lato opposto in segmenti proporzionali ai lati che lo comprendono (teorema della bisettrice). Le tre bisettrici di un triangolo si incontrano in un punto (detto incentro) che è il centro della circonferenza inscritta nel triangolo. Nel descrivere le proprietà dei triangoli, il termine bisettrice è anche utilizzato impropriamente per indicare ciascun segmento interno al triangolo staccato da ciascuna bisettrice. Si parla così di bisettrici di un triangolo e di lunghezza di ciascuna bisettrice di un triangolo. Se a, b, c sono i lati di un triangolo di semiperimetro p, allora la bisettrice del triangolo relativa all’angolo opposto ad a ha lunghezza
Analoghe le formule per la lunghezza delle altre bisettrici.