break-even analysis
break-even analysis
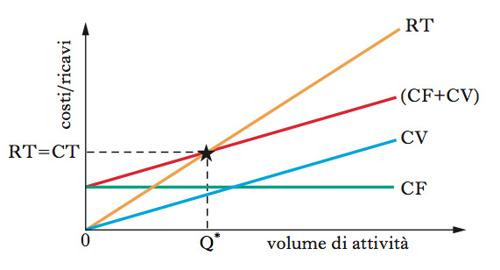
break-even analysis Esercizio di simulazione (dall’ingl. to break even «pareggiare i conti» o «chiudere in pareggio») condotto su un modello elementare, che consente di identificare il volume di attività in corrispondenza del quale si ha un utile pari a zero, ossia l’eguaglianza tra costi e ricavi (b.-e. point «punto di pareggio economico»).
Tale volume di attività può essere espresso in termini di quantità e di fatturato. La b.-e. a. è uno strumento del controllo di gestione (➔), che fornisce al management importanti informazioni per decidere, per es., quali linee produttive privilegiare/dismettere, quale politica di prezzi seguire, se realizzare internamente un prodotto/servizio o acquistarlo dall’esterno. Essa si fonda sull’assunzione che il volume di attività (la quantità di produzione e vendita) sia l’unico fattore in grado di influenzare in modo rilevante il comportamento dei costi, a loro volta disaggregati in variabili e fissi. In particolare, all’interno di un definito volume produttivo e in un orizzonte temporale di riferimento limitato, i primi variano al variare della quantità mentre i secondi rimangono costanti. Nel modello di base della b.-e. a., i metodi (matematici o grafici) per analizzare i costi assumono che quelli variabili si modifichino in modo proporzionale al variare della quantità. La domanda alla quale la b.-e. a. cerca di rispondere è quindi: quanti atti di vendita si devono realizzare per raggiungere il pareggio? Il metodo più semplice per determinare il punto di pareggio consiste nell’eguagliare i ricavi totali (RT) ai costi totali (CT), scomponendo questi ultimi in costi variabili (CV) e costi fissi (CF): RT=CV+CF. [1] Sapendo che i CF sono costanti e pari a K, che i RT corrispondono al prezzo di vendita (p) moltiplicato per la quantità (q) e che i CV sono dati dal costo variabile unitario (v) per la quantità (q), partendo dall’equazione [1] e risolvendo per (q) si può ricavare il b.-e. point in termini di quantità (Q*):Q*=K/(p−v). Q* esprime quindi la quantità da produrre e vendere per arrivare a coprire tutti i costi con i ricavi e conseguire un utile pari a zero; (p−v) viene detto margine di contribuzione unitario (➔ margine) e indica quanto residua dei ricavi di vendita per la copertura dei costi fissi o, in assenza di costi fissi da coprire, per la produzione di un margine di utile. Quindi, per es., per ogni unità venduta oltre Q* si avrà un utile che è pari al margine di contribuzione unitario.
Il b.-e. point in termini di fatturato (fatturato di pareggio, RT*) si può calcolare come: RT*=K/(1−v/p). Tra i principali limiti della b.-e. a. si ricordano: nella realtà spesso i costi fissi non sono costanti ma crescono ‘a gradini’ in corrispondenza di aumenti della capacità produttiva; i costi variabili non sempre sono legati ai volumi in modo direttamente proporzionale e inoltre cambiamenti nei volumi possono influenzare il livello dei costi variabili unitari; non si considera che variazioni di prezzo possono incidere sul livello della domanda e, quindi, dei volumi di vendita; si ignora la presenza di scorte di magazzino.