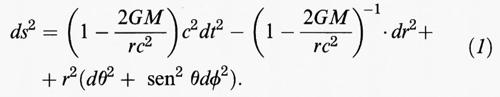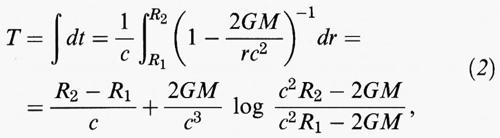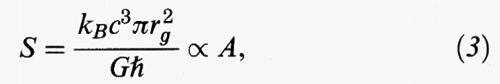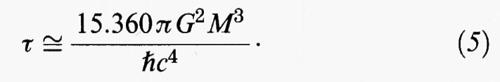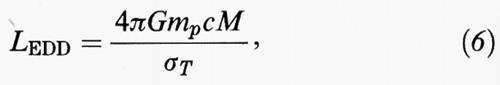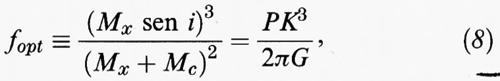Buchi neri

Buchi neri

Sommario: 1. Introduzione. 2. I buchi neri nella relatività generale. 3. Termodinamica dei buchi neri. 4. Proprietà dei buchi neri e macchine del tempo. 5. Formazione di buchi neri. □ 6. Prove osservative dell'esistenza di buchi neri: a) buchi neri supermassivi; b) buchi neri stellari. □ Bibliografia.

1. Introduzione

Il termine ‛buco nero' fu coniato nel 1967 da John Wheeler. Un buco nero può essere descritto, in termini di fisica newtoniana, come un corpo caratterizzato da massa M e dimensioni (raggio R) tali da avere alla sua superficie una velocità di fuga v_f = √2GM/R, uguale alla velocità della luce nel vuoto, c (la quantità G è la costante di gravitazione). La notizia della possibile esistenza di tali corpi compare per la prima volta nella letteratura scientifica in un lavoro di John Michell del 1783 e, indipendentemente, in un lavoro di Pierre-Simon Laplace del 1795. Michell e Laplace si resero conto che in corpi di data densità ρ e di raggi crescenti, la velocità di fuga alla superficie, √(8π/3)GρR², cresce indefinitamente, e, per raggi R = √3c²/ (8πGρ), essa diventa uguale alla velocità della luce. In termini della massa del corpo anziché della sua densità, il raggio limite diventa R = 2 GM/c². Invocando la natura corpuscolare della luce, Michell e Laplace conclusero che tale corpo sarebbe risultato incapace di emettere alcun segnale luminoso e, dunque, sarebbe apparso completamente nero.

Oggi sappiamo che la derivazione precedente non è esatta, poiché per buche di potenziale gravitazionale tanto profonde da verificare la condizione v_f = c, la fisica newtoniana cessa di essere valida e diviene necessaria una descrizione in termini della teoria della relatività generale di Einstein.

Nel 1916, con una lettera scritta dal fronte russo, poco prima della sua morte, Karl Schwarzschild rese nota la soluzione delle equazioni di Einstein che porta il suo nome. La soluzione di Schwarzschild descrive la metrica dello spazio-tempo all'esterno di un corpo sferico stazionario di massa data. Come vedremo nel seguito, in questa metrica esistono soluzioni che hanno proprietà analoghe al buco nero classico. Negli anni seguenti, furono trovate altre soluzioni delle equazioni di Einstein, adatte a descrivere corpi in rotazione e corpi elettricamente carichi. Queste soluzioni corrispondono ad altrettanti tipi diversi di buco nero. A causa della grande complessità delle equazioni di Einstein, i calcoli che portano a queste soluzioni sono molto laboriosi e le proprietà dei moti di materia in prossimità dei buchi neri sono tuttora oggetto di studio.

I buchi neri previsti dalla relatività generale sono oggetti stazionari e stabili, e le loro proprietà classiche sono descritte nel cap. 2. Non ci soffermeremo invece sulla trattazione quantistica, in quanto la mancanza di una soddisfacente teoria quantistica della gravitazione non permette di valutarne in modo definitivo le proprietà. Il fatto che l'orizzonte degli eventi di un buco nero funga da barriera dell'informazione, sottraendo all'osservatore esterno una zona di universo in precedenza osservabile, pone in modo naturale il problema dell'entropia di un buco nero. Nel cap. 3 sono esposti gli argomenti che portano ad attribuire a un buco nero grandezze termodinamiche come entropia e temperatura, descrivendone le conseguenze pratiche. La proprietà dei buchi neri di influenzare lo spazio-tempo nelle loro vicinanze può portare infatti a notevoli effetti osservativi. Nel cap. 4 vengono descritte alcune delle proprietà osservabili di un buco nero e la possibilità teorica di realizzare delle ‛macchine del tempo'. Nel cap. 5 vengono esaminati alcuni meccanismi che potrebbero portare alla formazione dei buchi neri, e nel cap. 6 si riassumono le varie prove osservative sull'esistenza dei buchi neri che, come si vedrà, è estremamente probabile, ma non è stata ancora provata. La sua conferma costituirebbe una forte evidenza a favore della validità della teoria della relatività generale. Infatti, mentre la teoria è stata verificata per campi gravitazionali deboli, per i quali causa una modifica relativamente piccola alle previsioni della gravitazione newtoniana, i buchi neri consentirebbero una verifica nel limite opposto dei campi gravitazionali forti.

2. I buchi neri nella relatività generale

Le soluzioni delle equazioni di Einstein sono espressioni per l'elemento di distanza metrica tra due punti infinitamente vicini dello spazio-tempo curvo. La metrica di Schwarzschild descrive lo spazio-tempo all'esterno di un corpo sferico di massa M posto nell'origine delle coordinate. In coordinate sferiche (t, r, θ, ϕ, dove t è il tempo, r la distanza radiale dall'origine del sistema di coordinate, θ l'angolo di declinazione e ϕ quello di azimut), essa ha la forma:

Nell'espressione (1), per la metrica di Schwarzschild, il coefficiente del differenziale radiale dr diventa infinito per r = r_g = 2GM/c². Tale raggio prende il nome di raggio di Schwarzschild. Il tempo necessario affinché un raggio di luce, emesso a una certa distanza R¹ ≥ r_g, raggiunga un osservatore lontano (cioè posto a distanza R₂ ≫ R₁) e a riposo, viene ricavato imponendo la condizione che la luce si muova lungo geodetiche nulle, ossia lungo il cammino caratterizzato da ds² = 0. Tale intervallo di tempo è dato da:

e diventa infinito quando la distanza di partenza si avvicina a r_g. Ciò significa che un raggio di luce emesso da un punto sulla superficie r = r_g impiegherà un tempo infinito per raggiungere un osservatore esterno. In altre parole, la regione interna a r_g non è accessibile all'osservazione dall'esterno. Di conseguenza, la sfera di raggio r_g prende il nome di ‛orizzonte degli eventi'. Qualunque corpo di massa M e raggio maggiore di r_g avrà un effetto al suo esterno descritto dalla metrica (1) e una metrica al suo interno dipendente dai dettagli della sua distribuzione di massa. Per un corpo di raggio pari a r_g o inferiore a tale valore, la metrica all'esterno di r_g è ancora descritta dall'espressione (1). Tuttavia, il corpo sarà contenuto entro il suo orizzonte degli eventi e non sarà osservabile dall'esterno.

L'orizzonte degli eventi non rappresenta una vera singolarità fisica. La singolarità di tale superficie esiste soltanto nel sistema di coordinate indipendenti dal tempo che sono state considerate. Cambiando sistema di coordinate, e scegliendone uno dipendente dal tempo (ad esempio, un sistema solidale con un corpo in caduta libera sul buco nero), non si riscontra alcuna singolarità per r = r_g; inoltre, le forze mareali a tale raggio rimangono finite e, per un buco nero supermassivo, sono molto piccole. In questo caso, un osservatore solidale con il nuovo sistema di riferimento mobile può accorgersi soltanto mediante misurazioni molto accurate di aver attraversato ciò che a un osservatore lontano appare invece come un orizzonte degli eventi. Avvicinandosi all'orizzonte, i segnali luminosi inviati dall'osservatore in caduta libera sarebbero ricevuti da osservatori posti a grande distanza dal buco nero spostati verso lunghezze d'onda via via sempre più lunghe (tale fenomeno è detto ‛spostamento verso il rosso'). Questa variazione di lunghezza d'onda è causata, in parte, da spostamento Doppler dovuto alla velocità relativa dei due osservatori e, in parte, da spostamento gravitazionale. Al contrario, l'osservatore in caduta riceverebbe i segnali inviati dall'osservatore a grande distanza sempre alla stessa lunghezza d'onda costante, poiché l'effetto Doppler compenserebbe in questo caso lo spostamento gravitazionale. In aggiunta a questi spostamenti di frequenza, l'osservatore all'infinito riceverebbe i messaggi dell'osservatore in caduta libera a intervalli temporali sempre più radi. L'osservatore in caduta libera attraverserebbe dopo un tempo finito, senza notare alcuna proprietà particolare, l'orizzonte degli eventi, e continuerebbe a precipitare in modo irreversibile sulla singolarità centrale (r = 0) senza avere la possibilità di invertire il proprio moto. L'osservatore posto all'infinito, invece, vedrebbe l'osservatore in caduta avvicinarsi sempre più all'orizzonte degli eventi, ma senza mai raggiungerlo o attraversarlo. Dal punto di vista della relatività generale, ossia trascurando effetti di meccanica quantistica, la singolarità a r = 0 è caratterizzata da forze di marea infinite. In contrasto con l'orizzonte, essa rappresenta una vera singolarità della metrica, ossia un punto caratterizzato da curvatura infinita. Una definizione più rigorosa, ma anche meno intuitiva di singolarità, è data nel testo di Misner, Thorne e Wheeler (v., 1973).

In relatività generale si può definire buco nero una qualunque soluzione stazionaria delle equazioni di Einstein con metrica fissata all'infinito (in generale piatta, ma sono stati studiati anche buchi neri in spazi non piatti all'infinito) che sia caratterizzata da un orizzonte degli eventi. Il principio di ‛censura cosmica' enunciato da Roger Penrose nel 1969, ma mai dimostrato, sancisce che in relatività generale non si possono avere singolarità ‛nude', ossia non protette all'osservazione dall'esterno da un orizzonte degli eventi. Torneremo nel cap. 4 ad analizzare il significato di questo principio. Per il momento ci limitiamo a osservare che se esso fosse sempre verificato, ogni soluzione stazionaria singolare delle equazioni di Einstein sarebbe un buco nero.

Nel 1917 e nel 1963 furono scoperte altre due soluzioni delle equazioni di Einstein descriventi buchi neri: la metrica di Reissner-Nordström e quella di Kerr. La principale differenza di questi buchi neri rispetto a quello di Schwarzschild consiste nel fatto che essi sono caratterizzati da altre grandezze fisiche in aggiunta alla massa. Il buco nero di Kerr rappresenta un buco nero rotante (ossia con momento angolare non nullo) e dotato di un asse di simmetria coincidente con l'asse di rotazione. Il buco nero di Reissner-Nordström rappresenta invece un buco nero con carica elettrica non nulla. È interessante notare che esistono dei teoremi, detti no-hair, i quali stabiliscono che un buco nero non può in generale essere caratterizzato da altre grandezze a parte la massa, il momento angolare e la carica elettrica. Da questo punto di vista, i buchi neri sono gli oggetti macroscopici più semplici che possano esistere, in quanto qualunque dettaglio della loro composizione interna è completamente irrilevante per gli osservatori esterni. Una descrizione esauriente di questi buchi neri si trova nella già citata opera di Misner, Thorne e Wheeler (v., 1973). Una descrizione matematica completa dei buchi neri si trova in Chandrasekhar (v., 1983).

3. Termodinamica dei buchi neri

L'origine degli studi termodinamici sui buchi neri risale a una domanda posta da Wheeler a Jacob Bekenstein (v., 1973), all'epoca suo studente. Il problema in discussione era quello dell'entropia, grandezza fisica che nell'universo non può che aumentare e che sappiamo essere connessa con la quantità di informazione. Chiunque compia un'azione aumentando l'entropia, commette, nelle parole di Wheeler, un ‛crimine', poiché modifica l'universo in modo irreversibile. Visto che l'orizzonte degli eventi rappresenta una superficie che non può essere attraversata da alcun tipo di osservazione, se si confinasse il materiale ad alta entropia in un volume limitato e lo si facesse cadere su di un buco nero riusciremmo a nascondere il nostro ‛crimine'? La risposta di Bekenstein fu negativa. I buchi neri hanno un'entropia proporzionale alla superficie del loro orizzonte degli eventi, data da:

dove k_B e ℏ sono, rispettivamente, le costanti di Boltzmann e di Planck, e A = 4π r²_g è la superficie del buco nero. Per l'equazione (3), qualunque materiale che cada in un buco nero, aumentandone la massa, ne aumenta la superficie e quindi l'entropia. L'idea di associare un'entropia a un buco nero non incontrò un favore immediato nella comunità scientifica. In effetti, l'entropia data dall'equazione (3) implica anche una temperatura data da:

Poiché in natura corpi a una data temperatura irraggiano energia in modo ben approssimato dalle leggi di corpo nero, anche un buco nero dovrebbe dunque irraggiare. Tuttavia, non sembrava plausibile che un buco nero potesse emettere energia, poiché l'unica direzione possibile per qualunque moto in tale corpo è dall'esterno verso l'interno, e non viceversa. Stephen Hawking fu uno dei ricercatori che, inizialmente con un atteggiamento scettico, studiò questo problema; finalmente, nel 1975, egli scoprì il cosiddetto meccanismo di Hawking (v., 1975) che, utilizzando effetti quantistici tuttora non completamente compresi, consentiva a un buco nero di irraggiare esattamente come un corpo nero ideale alla temperatura data dalla (4). Il dibattito sulla natura esatta e sulla modalità di irraggiamento di un buco nero non è ancora esaurito e vi sono nella comunità scientifica opinioni discordi. Il problema è reso più complesso dal fatto che anche qualora fosse scoperto un buco nero a distanze tali da renderlo suscettibile di osservazioni dettagliate dalla Terra, l'emissione prevista teoricamente sarebbe trascurabile, tranne nel caso in cui la massa del buco nero fosse molto piccola. Le possibilità di esistenza di tali buchi neri ‛ultraleggeri' sarà discussa più avanti.

4. Proprietà dei buchi neri e macchine del tempo

È un'opinione comunemente accettata che se fosse possibile attraversare l'orizzonte degli eventi e raggiungere la singolarità in un tempo finito (senza essere distrutti dalle forze mareali) si realizzerebbe una ‛macchina spazio-tempo' (v. Morris e altri, 1988). Una macchina spazio-tempo è un dispositivo che consente a un corpo di muoversi non solo in avanti nel tempo, come comunemente accade, ma anche indietro. La possibilità di compiere questo tipo di viaggi all'indietro nel tempo avrebbe notevoli implicazioni teoriche (e anche filosofiche) e per questo molti ricercatori hanno iniziato ad analizzare le equazioni di Einstein alla ricerca di soluzioni che consentano tale possibilità.

Il buco nero di Schwarzschild non rappresenta una macchina del tempo affidabile per due motivi principali: il primo di essi è che, dal punto di vista dell'osservatore lontano, sarebbe necessario un tempo infinito per raggiungere l'orizzonte degli eventi. Qualora l'osservatore in caduta sopravvivesse al viaggio e riuscisse a tornare al punto di partenza senza ripassare dal buco nero, l'osservatore lontano ne vedrebbe due immagini contemporaneamente, ossia quella che sta ancora cadendo sul buco nero e la nuova. In aggiunta, l'osservatore tornato a grande distanza dal buco nero potrebbe inviare e ricevere messaggi da se stesso mentre è ancora in caduta. Questo fatto rappresenterebbe una violazione della causalità. Il secondo problema del buco nero di Schwarzschild è dato dal fatto che le forze di marea sulla singolarità sono infinite, e dunque nessun osservatore reale sarebbe in grado di resistervi. Nei buchi neri più complessi di quello di Schwarzschild, come ad esempio nel buco nero di Kerr, vi sono regioni vicine alla singolarità dove sarebbe possibile effettuare viaggi nel tempo anche senza dover attraversare la singolarità. Se il principio di ‛censura cosmica' fosse dimostrato, tali regioni prossime alle singolarità sarebbero sempre protette da un orizzonte e in pratica inaccessibili. Minori inconvenienti presenterebbe una macchina del tempo che fosse priva non solo di singolarità infinite ma anche di un orizzonte degli eventi, in modo da consentire il viaggio da grandi distanze fino all'orizzonte in tempi finiti per gli osservatori distanti.

Una volta che la possibilità teorica di realizzare macchine del tempo fosse dimostrata in modo convincente, la stessa teoria della relatività generale sarebbe messa in discussione, poiché appare difficile conciliare l'esistenza di macchine del tempo con il principio di causalità. Non tutti i ricercatori condividono però questa interpretazione: ad esempio, è stato dimostrato (v. Friedman e altri, 1990) come sia possibile costruire delle soluzioni fisicamente accettabili nelle quali particelle elementari possono viaggiare nel tempo senza che il principio di causalità venga violato.

5. Formazione di buchi neri

Il fatto che le equazioni di Einstein prevedano l'esistenza dei buchi neri non implica necessariamente che essi esistano realmente. In effetti, le soluzioni descritte in precedenza descrivono buchi neri eterni, ossia che sono sempre esistiti e sempre esisteranno. È assai probabile che lo stesso processo di formazione di un buco nero, e in particolare del suo orizzonte degli eventi, richieda un tempo infinito dal punto di vista dell'osservatore lontano. In questo caso sarebbe possibile l'esistenza di un certo numero di buchi neri ‛fisici', ossia che approssimano in modo estremamente buono le soluzioni esatte delle equazioni di Einstein, ma di nessun buco nero ‛matematico'. Un osservatore in caduta sul buco nero assisterebbe alla formazione del buco nero in un tempo finito. Tuttavia, per il teorema di Birkhoff (che generalizza il teorema di Gauss e sancisce che i dettagli sulla distribuzione di materia per una distribuzione a simmetria sferica non influenzano il campo esterno), un osservatore all'infinito osserverebbe proprietà identiche a quelle del buco nero matematico. Pertanto, nel seguito, ignoreremo questa distinzione formale e considereremo solamente le problematiche fisiche inerenti la formazione di buchi neri. Per comodità, si distinguono in astrofisica tre classi di buchi neri a seconda delle loro masse e, di conseguenza, dei loro meccanismi di formazione.

Storicamente, il primo meccanismo di formazione di buchi neri preso in considerazione fu il collasso stellare. I primi a studiare questo processo furono J. R. Oppenheimer e H. Snyder nel 1939. Sappiamo oggi che stelle molto più massive del Sole terminano la loro evoluzione con una esplosione di supernova (di tipo II). Il nucleo della stella collassa su se stesso e raggiunge densità talmente alte da formare una stella di neutroni, ossia una stella in cui le forze di pressione che bilanciano la gravitazione sono fornite dal gas degenere di Fermi di neutroni. Sappiamo anche che le stelle di neutroni non possono avere una massa superiore alla cosiddetta massa di Chandrasekhar, pari a circa 1,4 ÷ 3 masse solari. Nonostante l'incertezza sul valore preciso di questa massa limite (dovuta principalmente alle incertezze sulla precisa equazione di stato della materia neutronica a densità supernucleari), è accertato che per masse superiori a circa 3 masse solari non esiste alcuna configurazione stabile rispetto al collasso gravitazionale. Per M ≥ 3 masse solari, il nucleo dunque collassa e forma un buco nero. Dal punto di vista fisico, questo significa che, non appena la gravità raggiunge valori tali da rendere instabile una configurazione sostenuta dalla pressione del gas di Fermi di neutroni, nessun'altra forza fisica è più in grado di arrestare il collasso. Lo scenario descritto appare abbastanza comprensibile dal punto di vista fisico, ma è tutt'altro che semplice effettuare calcoli dettagliati per studiare l'esplosione di una supernova e la formazione di buchi neri. In generale, si pensa che la massa di una stella che formi un buco nero, anziché una stella di neutroni, debba essere maggiore di 25 masse solari.

Un meccanismo alternativo di formazione di un buco nero è costituito dalla fusione delle due componenti di un sistema stellare binario, in cui entrambe le stelle siano stelle di neutroni. Un certo numero di questi oggetti dovrebbe esistere nella nostra Galassia e quattro possibili candidati sono stati studiati in dettaglio. In tutti questi sistemi stellari binari, una delle componenti è una stella pulsante (o pulsar), mentre l'altro oggetto è una seconda stella di neutroni, non pulsante. I sistemi binari studiati contenenti stelle di neutroni hanno periodi orbitali estremamente corti. Tali periodi si accorciano progressivamente a causa dell'emissione di onde gravitazionali che tende a ridurre la separazione tra le due componenti. La variazione di periodo osservata è in effetti una delle verifiche sperimentali della teoria della relatività generale. Nel momento in cui le due stelle di neutroni entrano in contatto, si ha un'esplosione estremamente violenta accompagnata da intensa emissione di radiazioni. Qualora l'energia emessa sia molto minore della massa (moltiplicata per la velocità della luce al quadrato) di una delle componenti, il residuo materiale dell'esplosione sarà una singola stella troppo massiva per poter rimanere una stella di neutroni. Questa collasserà ulteriormente, formando un buco nero. Si noti come, a parità di massa, il raggio di un buco nero e di una stella di neutroni differiscano solo per un fattore 2. Una volta che un buco nero stellare si è formato, è facile che esso aumenti di massa inglobando gas o altre stelle. In un tempo inferiore all'età dell'universo, un buco nero posto nel nucleo di una galassia tipica può crescere da dimensioni stellari fino a vari milioni o anche miliardi di masse solari, corrispondenti a raggi di Schwarzschild superiori al raggio dell'orbita terrestre.

Un altro meccanismo di formazione di buchi neri supermassivi potrebbe essere il collasso diretto di una massa di gas molto grande nel nucleo di una protogalassia. Sfortunatamente, questo processo è molto complesso da studiare teoricamente e non sappiamo al momento attuale se si verifichi effettivamente.

Buchi neri di massa molto inferiore a una massa solare potrebbero essersi formati nelle prime fasi di espansione immediatamente successive all'origine dell'universo (big bang; v. relatività: Gravitazione e cosmologia). La massa di tali oggetti potrebbe essere molto piccola. Tuttavia, poiché la temperatura di un buco nero è inversamente proporzionale alla sua massa, a causa dell'emissione di Hawking, un buco nero irraggia tutta la sua massa in un tempo

Tale limite, molto maggiore dell'età dell'universo per buchi neri di massa stellare, è uguale all'età dell'universo quando M ≅ 10¹² kg. Buchi neri meno massivi di tale valore, anche se si fossero formati durante il big bang, sarebbero oggi evaporati completamente. Mini-buchi neri di massa maggiore di 10¹² kg potrebbero invece esistere tutt'oggi ed essere in lenta evaporazione. Il fatto che la radiazione cosmica di fondo abbia uno spettro estremamente prossimo a quello di un corpo nero ideale, permette di porre dei limiti stringenti al numero massimo di mini-buchi neri che possono essere esistiti. Infatti, i mini-buchi neri emettono radiazione estremamente energetica prima di evaporare completamente. Tale radiazione sarebbe in grado di distorcere lo spettro della radiazione cosmica di fondo.

6. Prove osservative dell'esistenza di buchi neri

Analizziamo ora quali sono le prove osservative dell'esistenza di buchi neri, sia di massa stellare che supermassivi; per entrambi, il principio che si utilizza è la misurazione degli effetti gravitazionali del buco nero sul moto di stelle o di gas che si trovano nelle sue vicinanze. Altre tecniche di ricerca, ad esempio basate sulla rilevazione di valori estremi di spostamento verso il rosso di natura gravitazionale, non hanno finora avuto successo.

a) Buchi neri supermassivi

L'esistenza di buchi neri supermassivi è stata inizialmente dedotta in modo indiretto dalle proprietà delle quasar e dei nuclei galattici attivi (v. quasar; v. Rees, 1984). Tali oggetti sono caratterizzati da enormi luminosità originate in regioni estremamente ridotte, in cui l'energia di legame gravitazionale è dunque assai ingente. Vari autori hanno mostrato come un nucleo galattico attivo finirebbe immancabilmente per formare al suo interno un buco nero supermassivo, anche se inizialmente non ne ospitasse alcuno. Le stime di massa per i buchi neri supermassivi in quasar e nuclei attivi derivano principalmente da misurazioni indipendenti di dimensioni e di velocità. Le velocità si ricavano dall'osservazione della larghezza delle righe spettrali di emissione di tali oggetti e raggiungono in vari casi valori di 5.000 km/s. Le dimensioni sono stimate sulla base di modelli dettagliati, oppure tramite l'osservazione della variabilità nella luminosità totale. Infatti, assumendo che la variabilità sia un fenomeno coerente che coinvolge tutto il nucleo attivo, quando si osserva una variabilità su tempi scala dell'ordine di Δt secondi, si può dedurre una dimensione minore di cΔt, che è il tempo necessario alla luce per attraversare il nucleo stesso. I valori che si ottengono per le masse dei buchi neri sono in genere dell'ordine di 10 milioni di masse solari.

Una diversa stima di massa per un nucleo galattico attivo si ottiene richiedendo che la sua luminosità non superi un valore critico, detto luminosità di Eddington (L_EDD). Questa è la luminosità alla quale la pressione di radiazione su di un plasma di idrogeno completamente ionizzato supera la forza di attrazione gravitazionale. Nel caso di simmetria sferica si ha:

dove m_p = 1,673 × 10^-27 kg è la massa del protone e σ_T = 0,665 × 10^-28 m² è la sezione d'urto di Thomson.

Poiché si pensa che la sorgente primaria di energia dei nuclei galattici attivi sia la conversione in radiazione dell'energia gravitazionale della materia che si trova nelle vicinanze del buco nero centrale supermassivo, è necessario che la luminosità del buco nero sia inferiore alla sua luminosità di Eddington. In caso contrario, la pressione della radiazione bloccherebbe l'accrescimento di materia e ridurrebbe la luminosità del nucleo. Malgrado l'accrescimento non avvenga a simmetria sferica, si ritiene che la luminosità di Eddington sia un valore assai significativo. In effetti, le stime di massa ricavate dagli allargamenti delle righe spettrali sono in accordo con le stime basate sulla luminosità data dall'equazione (6).

Sebbene il quadro appena descritto abbia molte verifiche sperimentali indirette, non vi sono nuclei attivi per i quali l'esistenza di un buco nero sia assolutamente ineluttabile e, inoltre, le argomentazioni precedenti dipendono in qualche misura da considerazioni teoriche. Per questo motivo si sono cercate prove decisive dell'esistenza dei buchi neri supermassivi nei nuclei di galassie vicine (v. sistemi stellari), dove le nostre osservazioni hanno una maggiore risoluzione spaziale. Osservando spettroscopicamente i nuclei delle galassie è possibile misurare i moti delle stelle e del gas in tali regioni. Misurando la velocità di rotazione delle stelle o del gas, o la dispersione della velocità stellare v a una distanza R dal nucleo, è possibile stimare la massa del nucleo stesso:

dove ξ è una costante dell'ordine dell'unità che dipende dagli effetti geometrici di proiezione e dal modello adottato per i moti del gas e delle stelle. La vera difficoltà di questo tipo di studi consiste proprio nel ridurre al minimo l'incertezza sul valore della costante ξ o, almeno, di ottenere un limite inferiore per essa che si tradurrebbe in un limite inferiore per la massa. La densità media del nucleo risulta essere ρ ≅ 3M/(4π R³). In generale, i valori della densità centrale che si ottengono in questo tipo di studi sono ben lontani dall'implicare necessariamente la presenza di un buco nero e tutte le osservazioni sarebbero ugualmente spiegabili con modelli ad hoc irrealistici e in equilibrio instabile, improbabili dunque da osservare ma non impossibili. Quindi, la forza di questo tipo di argomento non è tanto quella di isolare un unico oggetto che potrebbe trovarsi in uno stato molto particolare, quanto quella di mostrare come valori molto elevati di densità siano comuni a molte galassie e che per questo sarebbe estremamente improbabile che fossero tutti osservati da noi in un istante particolare della loro evoluzione. Candidati buchi neri supermassivi esistono nella nostra Galassia, nella galassia Messier 31 di Andromeda e in varie altre galassie situate entro 30 milioni di parsec (1 parsec = 3 × 10¹⁶ m) da noi. Di recente, si sono avute due ulteriori verifiche molto significative. Il telescopio spaziale Hubble (HST) ha osservato il nucleo della radiogalassia centrale nell'ammasso della Vergine (Virgo A = Messier 87 = NGC 4486), in cui l'esistenza di un buco nero fu teorizzata in modo convincente già nel 1978. Le osservazioni HST hanno mostrato come una massa di 3 miliardi di masse solari sia concentrata entro 14 parsec (0,2 secondi d'arco alla distanza di 18 milioni di parsec) dal centro di M87. Tuttavia, il raggio di Schwarzschild di un buco nero di 3 × 10⁹ masse solari è 6 × 10^-5 parsec, e dunque molto inferiore alle dimensioni esplorate con HST. È difficile pensare come la fenomenologia osservata in M87 possa essere spiegata da qualcosa di diverso da un buco nero supermassivo. La seconda osservazione è ancora più spettacolare. Nel centro della galassia attiva NGC 4258 è stato osservato un disco di gas in rotazione rapida ed emittente radiazione maser (v. Miyoshi e altri, 1995). Le osservazioni, alla lunghezza d'onda di 1,3 cm, sono state condotte con un radiotelescopio interferometrico costituito da varie antenne poste in diversi paesi del mondo, tra cui gli Stati Uniti e il Giappone. Esse hanno rivelato che, a distanze di circa 0,13 parsec dal centro di NGC 4258, il gas ruota alla velocità di circa 1.000 km/s. La variazione della velocità di rotazione con la distanza è esattamente quella prevista se nel nucleo fosse presente un buco nero della massa di 3,6 × 10⁷ masse solari.

b) Buchi neri stellari

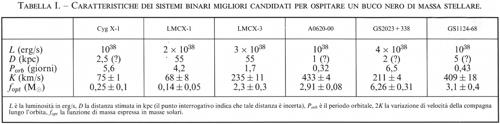
La possibile esistenza di buchi neri di massa stellare nella nostra Galassia è stata oggetto di numerose ricerche. A partire dalle osservazioni di Cygnus X-1 sono stati proposti vari altri candidati buchi neri. In genere questi oggetti vengono cercati tra sistemi binari emittenti raggi X. Tali sistemi sono formati da una stella di grande massa (HMXRB, High Mass X-Ray Binary) o di piccola massa (LMXRB, Low Mass X-Ray Binary), in orbita con una compagna compatta. La compagna compatta è generalmente una stella di neutroni. In alcuni casi, tuttavia, l'evidenza diretta derivante dalla massa della compagna, o quella indiretta derivante dalle proprietà dettagliate del sistema, sono incompatibili con la presenza di una stella di neutroni, la cui massa limite è non superiore a circa 3 masse solari. In questi casi, si pensa che la stella compagna sia in realtà un buco nero. Dunque, in contrasto con il caso dei buchi neri supermassivi, la dinamica delle stelle binarie può essere studiata in modo accurato. L'incertezza sulla reale presenza di buchi neri in questi sistemi dipende in modo critico da quale sia il valore massimo per la massa di una stella di neutroni o, eventualmente, di altre configurazioni stellari compatte ma non collassate. Il limite di 3 masse solari lascia circa una dozzina di candidati buchi neri finora identificati nella nostra Galassia. Poiché tutte le stelle di neutroni la cui massa è stata misurata con precisione hanno una massa di 1,4 ± 0,1 masse solari, è assai probabile che l'insieme dei sistemi binari contenenti stelle di massa compresa tra 1,5 e 3 masse solari nasconda in realtà altri sistemi con buco nero. I sistemi binari miglior candidati per ospitare un buco nero di massa stellare sono elencati nella tab. I (v. McClintock, 1991; v. Casares e altri, 1992; v. Remillard e altri, 1992). La quantità f_opt che compare nella tab. I è la cosiddetta funzione di massa, definita come:

dove M_x e M_c sono, rispettivamente, le masse della componente X e della compagna ottica, i è l'angolo di inclinazione dell'orbita, P è il periodo dell'orbita e K l'ampiezza di velocità. Poiché f_opt è una grandezza misurabile, se si hanno delle stime sulla massa della compagna M_c, basate, ad esempio, su studi spettrali e sulla sua luminosità ottica (v. stelle, vol. VII) e sull'inclinazione dell'orbita, si riesce a ottenere un valore per la massa M_x del candidato buco nero. Per alcuni oggetti come A0620-00, GS2023+338 e GS1124-68, si ritiene che la massa M_c della compagna (assai debole) sia completamente trascurabile rispetto a M_x. In questo caso, la funzione di massa diviene un limite inferiore per la massa M_x. Da questo punto di vista, dunque, GS2023+338 rappresenta il miglior candidato buco nero noto.

BIBLIOGRAFIA

Bekenstein, J. D., Black holes and entropy, in ‟Physical review. D", 1973, VII, pp. 2333-2346.

Casares, J., Charles, P. A., Naylor, T., A 6,5-day periodicity in the recurrent nova V 404 Cygni implying the presence of a black hole, in ‟Nature", 1992, CCCLV, pp. 614-617.

Chandrasekhar, S., The mathematical theory of black holes, Oxford 1983.

Ford, H. C., Harms, R. J., Tsvetanov, Z. I., Hartig, G. F., Dressel, L. L., Kriss, G. A., Bohlin, R. C., Davidson, A. F., Margon, B., Kochhar, A. K., Narrowband HST images of M 87: evidence for a disk of ionized gas around a massive black hole, in ‟The astrophysical journal letters", 1994, CDXXXV, 2, pp. L27-L30.

Friedman, J., Morris, M. S., Novikov, I. D., Echeverria, F., Klinkhammer, G., Thorne, K. S., Yurtsever, U., Cauchy problem in spacetimes with closed timelike curves, in ‟Physical review. D", 1990, XLII, pp. 1915-1930.

Hawking, S. W., Particle creation by black holes, in ‟Communications in mathematical physics", 1975, XLIII, pp. 199-200.

McClintock, J., Black holes in the galaxy, in Texas/ESO-CERN symposium on relativistic astrophysics, cosmology and fundamental physics (a cura di J. D. Barrow, L. Mestel e P. A. Thomas), New York 1991, pp. 495-502.

Misner, C. W., Thorne, K. S., Wheeler, J. A., Gravitation, New York 1973.

Miyoshi, M., Moran, J., Herrnstein, J., Greenhill, L., Nakai, N., Diamond, P., Inoue, M., Evidence for a black hole from high rotation velocities in a sub-parsec region of NGC 4258, in ‟Nature", 1995, CCCLXXIII, pp. 127-129.

Morris, M. S., Thorne, K. S., Yurtsever, U., Wormholes, time machines, and the weak energy condition, in ‟Physical review letters", 1988, LXI, pp. 1446-1449.

Rees, M. J., Black hole models for active galactic nuclei, in ‟Annual review of astronomy and astrophysics", 1984, XXII, pp. 471-506.

Remillard, R. A., McClintock, J. E., Bailyn, C. D., Evidence for a black hole in the X-ray binary nova Muscae 1991, in ‟The astrophysical journal letters", 1992, CCCIC, pp. L145-L149.