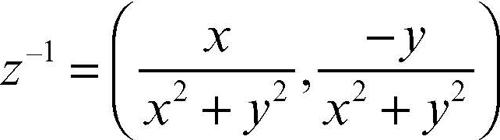C (insieme dei numeri complessi)

C (insieme dei numeri complessi)

C (insieme dei numeri complessi) insieme numerico, indicato con il simbolo C, che costituisce un ampliamento dell’insieme dei numeri reali R attraverso l’introduzione dell’unità immaginaria i, definita come il numero tale che i² = −1. Un numero complesso z è generalmente scritto nella forma x + iy, dove x e y sono numeri reali. Formalmente C può quindi essere definito come l’insieme R² = R × R costituito dalle coppie ordinate di numeri reali (x, y) e dotato delle due operazioni di addizione (indicata con il simbolo +) e moltiplicazione (indicata con il simbolo ⋅) definite rispettivamente da:

• (x_1, y₁) + (x₂, y₂) = (x₁ + x₂, y₁ + y₂)

• (x_1, y₁) ⋅ (x₂, y₂) = (x₁x₂ − y₁y₂, x₁y₂ + y₁x₂)

Le due operazioni sono entrambe associative e commutative e valgono le proprietà distributive; inoltre ammettono entrambe elemento neutro: l’elemento neutro dell’addizione è (0, 0), più semplicemente denotato con il simbolo 0, quello della moltiplicazione è (1, 0), più semplicemente indicato con 1; per ogni elemento z = (x, y) è poi definito il suo opposto (o inverso additivo) −z = (−x, −y) e ciò permette di definire la sottrazione tra numeri complessi. Per ogni elemento z = (x, y) diverso da 0 è anche definito il suo inverso (inverso moltiplicativo)

e ciò permette di definire la divisione tra numeri complessi. Con le due operazioni di addizione e moltiplicazione, l’insieme R² acquisisce la struttura di campo, è detto insieme dei numeri complessi ed è indicato con il simbolo C.

Il sottoinsieme di C costituito dalle coppie della forma (x, 0) è isomorfo all’insieme R dei numeri reali: in altri termini, dopo aver identificato il numero reale x con il numero complesso (x, 0), restringendo al sottoinsieme costituito dagli elementi di questa forma le operazioni di addizione e moltiplicazione definite in C, si ottengono le usuali operazioni di addizione e moltiplicazione definite in R. In questo senso, si dice che C è un → ampliamento di R. Il campo C non è ordinato, ossia non esiste alcun ordinamento totale su C che sia compatibile con la sua struttura di campo; pertanto non si può dire se un numero complesso è «minore» o «maggiore» di un altro e non ha senso perciò scrivere disuguaglianze tra numeri complessi.

L’insieme R² ha una naturale struttura di spazio vettoriale su R. Questa ulteriore struttura algebrica viene ereditata da C e in essa i due elementi 1 = (1, 0) e i = (0, 1) costituiscono la base canonica di R² in quanto, come già detto, ogni numero complesso (x, y) può essere scritto nella forma (x, 0) + (0, y) = x(1, 0) + y(0, 1) = x + iy, che è la forma più comunemente usata. Come insieme di coppie ordinate di numeri reali, l’insieme dei numeri complessi ammette anche una rappresentazione geometrica (→ Argand-Gauss, piano di). Dal fatto che, per costruzione, −1 possiede una radice quadrata in C, segue che ogni numero complesso diverso da 0 (e in particolare ogni numero reale non nullo, positivo o negativo che sia) ammette due radici quadrate complesse: questa è la proprietà che più distingue il campo C dei numeri complessi dal campo R dei numeri reali, dove un quadrato non è mai negativo. Più in generale, ogni equazione polinomiale a coefficienti reali possiede un numero di soluzioni complesse che, contate con la rispettiva molteplicità, coincide con il grado dell’equazione stessa: questo fatto si esprime dicendo che C è un campo algebricamente chiuso (teorema fondamentale dell’algebra). D’altra parte, poiché per costruzione i è algebrico su R (→ elemento algebrico), ogni numero complesso è algebrico su R: pertanto C è la chiusura algebrica di R.

Per la norma di un numero complesso si veda il lemma → numero complesso, norma di un.

lettC_00050.rtf