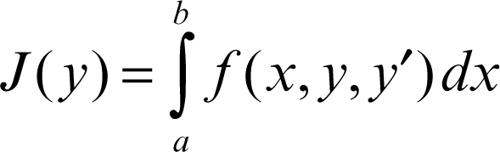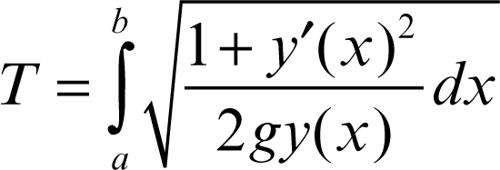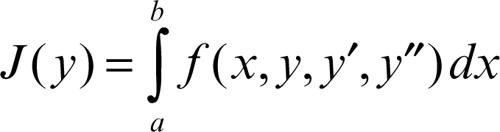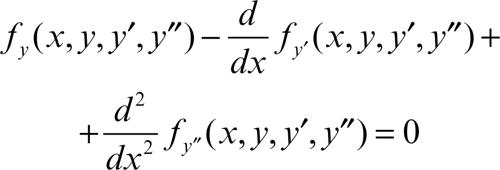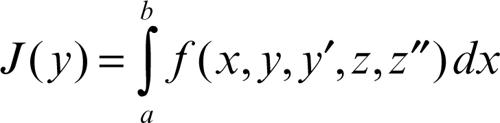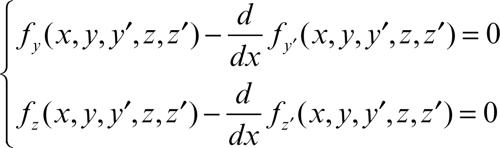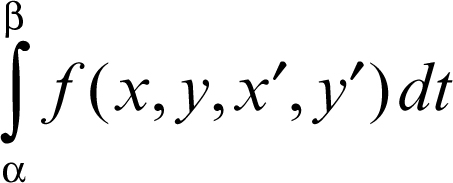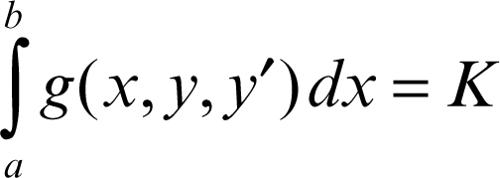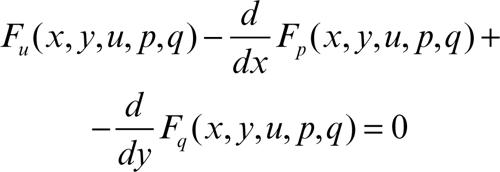variazioni, calcolo delle

variazioni, calcolo delle

variazioni, calcolo delle branca dell’analisi matematica che studia problemi di massimo o di minimo relativi non tanto a funzioni di una grandezza numericamente variabile ma a funzioni dipendenti da curve o da altre funzioni, dette in genere funzionali e definiti su assegnati spazi di funzioni. Il calcolo delle variazioni ha portato alla risoluzione di classici problemi di massimo e di minimo, quali per esempio il problema di determinare la più breve linea che si possa tracciare su una data superficie e che congiunga due punti di essa (problema della geodetica) o quello di determinare la linea congiungente due punti, percorsa nel minor tempo possibile da una massa concentrata in un punto e soggetta alla gravità (problema della brachistòcrona). Applicato forse per la prima volta da J. Bernoulli per trovare appunto la curva brachistòcrona, il calcolo delle variazioni ha interessato tutti i grandi matematici del xviii secolo, da Eulero a Lagrange a Weierstrass, ed è all’origine della moderna analisi funzionale.

Il caso più semplice di calcolo delle variazioni consiste nello studio del funzionale

Si tratta di trovare, tra tutte le funzioni

quella per cui l’integrale dato risulti minimo o massimo. A tale equazione si associa in generale un → problema ai limiti, quale, per esempio, il passaggio per due punti A(a, y₁) e B(b, y₂). Per esempio, il tempo di caduta di un grave che dà luogo al problema della → brachistòcrona è dato da

Si mostra che una soluzione, se è di classe C ², soddisfa l’equazione di → Eulero-Lagrange:

dove d /dx è la derivata totale che, sviluppata, dà l’equazione differenziale del secondo ordine

Le soluzioni sono dette estremali e corrispondono a punti di stazionarietà del funzionale. C. Jacobi, K. Weierstrass e A. Kneser hanno individuato diverse condizioni necessarie e/o sufficienti affinché una soluzione estremale sia anche estremante, cioè realizzi effettivamente un massimo o un minimo.

Il funzionale J si può generalizzare in diversi modi:

• modificando le condizioni ai limiti. Per esempio, imponendo che il secondo estremo stia sulla linea Γ di equazione y = γ(x), si impone la cosiddetta condizione di trasversalità:

Nel caso, importante, in cui Γ abbia espressione x = β(y), si pone γ′ = 1/β′ e si ottiene

Per esempio, se il secondo estremo sta sulla retta x = h, si ha β′ = 0 e quindi si imporrà

La condizione di trasversalità, nel caso in cui ƒ ha la forma

si traduce nella condizione di ortogonalità tra la linea estremale e il vincolo;

• introducendo derivate successive: nel caso

si ha l’equazione di → Eulero (del quarto ordine)

• facendolo dipendere da una linea nello spazio. Se

si ottiene il sistema di equazioni

Se la linea è espressa in forma parametrica, x = x(t), y = y(t), α ≤ t ≤ β, si dovrà rendere estremo il funzionale

dove si deve supporre che la funzione ƒ soddisfi la condizione ƒ(x, y, kx′, ky′ ) = kƒ(x, y, x′, y′ ) per k > 0, cioè che risulti positivamente omogenea di primo grado rispetto alle ultime due variabili, in modo che l’integrale non dipenda dalla rappresentazione parametrica della linea. Sotto questa ipotesi, il sistema delle due equazioni che si dovrebbero scrivere avendo due incognite x e y si riduce all’unica equazione

dove F è la funzione che soddisfa le uguaglianze

e che esiste per la condizione di omogeneità richiesta. L’equazione determina la linea estremale, ma non la sua parametrizzazione, per ottenere la quale si deve aggiungere una condizione supplementare largamente arbitraria.

Importante è il cosiddetto teorema isoperimetrico, secondo il quale la linea chiusa di assegnata lunghezza che racchiude l’area massima è la circonferenza. Dualmente, si dimostra che la linea di lunghezza minima che racchiude un’area assegnata è la circonferenza. Questo risultato è un caso particolare di problema vincolato: si cerca il massimo di un funzionale J(y) con un vincolo del tipo

È possibile adattare a questi problemi il metodo dei moltiplicatori di Lagrange.

Un altro problema classico è quello delle linee di lunghezza minima (→ geodetica) su una assegnata superficie S. Si mostra che le linee estremali godono della proprietà che la loro normale principale coincide in ogni punto con la normale alla superficie. Una più ampia generalizzazione si ha quando l’incognita risulta funzione di due variabili indipendenti definita in un insieme Ω; il funzionale assume allora la forma

dove p = u_x e q = u_y sono abbreviazioni consuete per le derivate parziali. Le condizioni accessorie consistono in un problema al contorno, come il problema di → Dirichlet o quello di → Neumann.

L’equazione delle estremali è talvolta detta di Eulero-Ostrogradskij, dal nome di Eulero e del matematico e fisico ucraino M.V. Ostrogradskij. Essa ha la forma

Per esempio, l’energia di un campo di potenziale u è data da

e l’equazione che si ottiene è quella di → Laplace. Il fatto che la soluzione di tale equazione soddisfacente un dato problema di Dirichlet renda effettivamente minimo l’integrale è noto come principio di Dirichlet. Per la superficie di area minima il funzionale è

(→ Plateau, problema di). La generalizzazione a più di due variabili è immediata. Una difficoltà teorica del calcolo delle variazioni consiste nel fatto che l’esistenza della soluzione non è sempre assicurata in C ¹; per esempio, il funzionale

con le condizioni y(−1) = y(1) = 1 non ammette minimo tra le funzioni di classe C ¹, pur assumendo valori positivi comunque piccoli; il minimo infatti si raggiunge sulla spezzata y = ⃒x⃒. Deve dunque essere specificato meglio lo spazio funzionale dove si cerca la soluzione (e quindi anche il senso da dare all’integrale).

I metodi diretti del calcolo delle variazioni cercano di risolvere il problema mediante l’uso di opportune successioni minimizzanti {u_n}, tali che i valori J (u_n) siano decrescenti e tendano all’estremo inferiore dei valori assunti dal funzionale. Tali metodi, che devono essere inquadrati in opportuni spazi topologici, consentono sia di dimostrare l’esistenza del minimo, quando sussiste, sia di determinare approssimazioni adatte al calcolo numerico. Condizioni sufficienti sono state date da L. Tonelli e fanno uso della nozione di semicontinuità del funzionale.

Negli ultimi decenni il calcolo delle variazioni si è occupato principalmente di determinare punti critici di funzionali con metodi topologici, mostrando cioè che livelli del funzionale che risentono di un cambiamento di topologia vengono di fatto assunti in un appropriato spazio funzionale generando quindi punti critici e a fortiori soluzioni del problema originario: il problema più importante in questo contesto è il cosiddetto problema di compattezza e precisamente quando poter garantire che una successione estremale, per esempio minimizzante, di fatto converge.

approfondimento