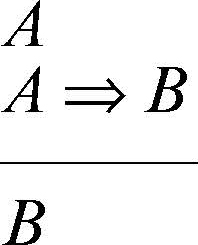calcolo logico

calcolo logico

calcolo logico locuzione che indica un sistema formale in cui è possibile tradurre rigorosamente il concetto di → dimostrazione. Ogni ragionamento formulato nel linguaggio naturale si compone di una serie di affermazioni che discendono l’una dall’altra in modo che da alcune premesse si possa giungere a una conclusione. In un calcolo logico tale procedimento viene formalizzato attraverso regole che sono dette regole di inferenza o regole di deduzione; applicando tali regole si può creare una catena di deduzioni che, a partire dagli assiomi del sistema formale, conduca a una nuova formula ben formata, che riveste il ruolo di conclusione del ragionamento. Per esempio, il ragionamento «Franco oggi non lavora; se Franco non lavora, va al mare; quindi oggi Franco va al mare» può essere formalizzato dalla regola di deduzione detta modus ponens che si esprime simbolicamente nel modo seguente:

In tale espressione: la proposizione «Franco non lavora» viene indicata dalla lettera A; la proposizione «Franco va al mare» viene indicata da B; l’espressione simbolica A ⇒ B (implicazione) corrisponde a «se Franco non lavora, va al mare»; la linea orizzontale separa le premesse dalla conclusione («Franco va al mare»).

Il concetto di dimostrazione, così com’è codificato in un calcolo logico, si differenzia in parte da ciò che s’intende per dimostrazione nella pratica matematica. Nei calcoli logici, infatti, ogni catena deduttiva deve partire dagli assiomi e, per mezzo delle regole di inferenza, arrivare alle conclusioni giustificando tutti i passaggi deduttivi, anche quelli che appaiono di immediata evidenza. Una dimostrazione matematica, invece, non ricalca sempre, in maniera fedele e invariabile, questo schema. Tuttavia, l’importanza dei calcoli logici risiede altrove, ovvero nella capacità di formalizzare il ragionamento. Questo problema affonda le sue radici nell’antichità; in particolare le opere di logica di Aristotele, in seguito riordinate e raccolte con il titolo Organon, sono state considerate, per molti secoli, una definitiva sistemazione della scienza del ragionare. I tipi più elementari di ragionamento che egli esamina sono i sillogismi. Nella logica medievale si guarda sempre più alla forma del ragionamento con un’esigenza di rigore, frutto della ricerca di uno strumento “imparziale” che porti ad analizzare la struttura formale dei ragionamenti e a utilizzare in tali analisi espressioni simboliche al posto di espressioni verbali. Così, accanto all’indagine dei procedimenti che sono alla base del ragionamento, si sviluppa la ricerca di un linguaggio simbolico in cui esprimere tali procedimenti. Da ciò nasce la graduale analogia con il calcolo. Un procedimento di manipolazione simbolica attraverso regole che consentono il rimpiazzo di una forma con un’altra è, infatti, del tutto analogo a un processo di calcolo, di trasformazione di un’espressione in un’altra. Il consolidamento dell’aspetto simbolico della logica e dell’utilizzo di un procedimento di calcolo per esprimere qualsiasi inferenza si ha nel xvii secolo con G.W. Leibniz e nel secolo successivo con G. Boole che, nella sua Analisi matematica della logica, introduce un vero e proprio calcolo logico, chiarendo come la validità di un procedimento non risieda in alcuna possibile interpretazione dei simboli, ma unicamente nelle leggi che li combinano fra loro. Esempi di calcolo logico sono il calcolo delle → proposizioni, detto anche calcolo degli enunciati, il calcolo dei → predicati e il calcolo dei → sequenti.