call option

call option

Titolo derivato che incorpora il diritto, ma non l’obbligo, di colui che lo detiene a comperare da una controparte, contrattualmente obbligata, una certa quantità di un asset sottostante (A; ➔ opzione, tipologia di p), a un prezzo prefissato, a una certa epoca precisa o entro una certa epoca. La posizione del titolare del diritto è definita posizione lunga, quella della controparte posizione corta (➔ posizione). Il prezzo di acquisto prefissato è detto prezzo di esercizio (in gergo strike, K), il termine del diritto è definito scadenza o maturità dell’opzione (T). L’opzione esercitabile esclusivamente a scadenza è di tipo europeo, quella esercitabile in qualsiasi epoca precedente la scadenza è di tipo americano.

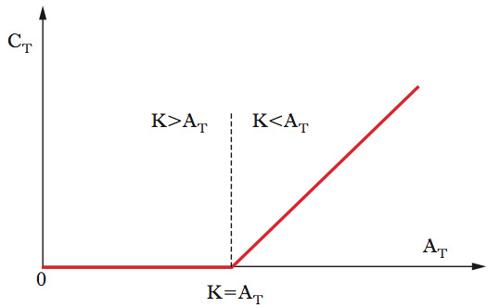
Valutazione alla scadenza di una call option

Il valore a scadenza (detto anche saldo netto o pay off) di una c. o. è la differenza tra il prezzo a scadenza del sottostante e il prezzo di esercizio, quando essa sia positiva; 0 altrimenti. In simboli: C_T=max(A_T−K, 0). Il saldo netto, dunque, è pari alla differenza tra il prezzo a scadenza dell’attività sottostante e il prezzo di esercizio, se tale differenza è positiva; in caso contrario, il saldo netto è nullo. Infatti, se (A_T−K)>0, al detentore dell’opzione conviene esercitarla, perché pagando il prezzo di esercizio K, riceverà un bene di valore A_T superiore, che potrà immediatamente rivendere lucrando la differenza (A_T−K). Tale differenza rappresenta allora il saldo netto dei movimenti a scadenza (➔ anche opzioni europee). Viceversa, nel caso (A_T−K)<0, il detentore lascerà scadere (o spirare) l’opzione senza esercitarla. Ciò è esemplificato dalla raffigurazione geometrica in un sistema cartesiano con i valori dei prezzi in ascissa e il valore del saldo netto a scadenza in ordinata. Quanto detto vale al momento della scadenza sia per un’opzione europea sia per una americana non ancora esercitata; alla scadenza quest’ultima è perfettamente equivalente alla gemella europea.

Valutazione in epoca precedente alla scadenza

In epoca precedente alla scadenza il prezzo teorico si calcola con il metodo di arbitraggio. Esso fa entrare in gioco l’evoluzione aleatoria del prezzo del sottostante in un mondo ‘neutrale al rischio’, descrizione convenientemente aggiustata o deformata del mondo reale. In tale mondo, il prezzo di una c. o. europea è il valore attuale medio del valore aleatorio a scadenza dell’opzione stessa. Nella particolare ipotesi che, in tale mondo, il prezzo a scadenza del sottostante sia una variabile aleatoria con distribuzione lognormale, vale la formula di Black-Scholes (➔ Black-Scholes, formula di). Il prezzo di una c. o. americana, priva di costi e frutti almeno fino alla scadenza, coincide con quello della omologa c. o. europea (➔ anche opzioni americane).

Posizioni nella call option

Chi assume una posizione lunga in una c., paga alla stipula del contratto il prezzo corrente della stessa, puntando sul rialzo del prezzo del sottostante; al contrario chi sceglie una posizione corta, spera in un ribasso. La posizione corta procura un introito iniziale ma espone al rischio del rialzo. I sottostanti più comuni di una c. o. sono un titolo azionario, un titolo obbligazionario, una valuta, una merce, un indice. Quando il sottostante è un tasso di interesse l’opzione si chiama cap (➔). L’opzione tipica con un profilo standard del payoff è detta in gergo plain vanilla (➔ opzioni vanilla); esistono anche varianti, dette opzioni esotiche (➔), con profili di payoff più complessi: la c. contanti o niente, la c. asset o niente, la c. retrospettiva (look back).