cammino

cammino

cammino termine che assume diversi significati a seconda del contesto.

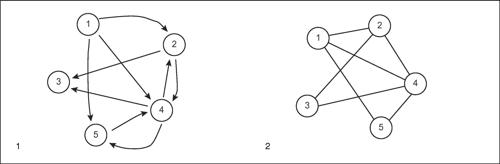
☐ In teoria dei grafi, si parla di cammino in un grafo orientato G(X, A), definito da un insieme X di nodi e un insieme A di archi, come di una sequenza finita di nodi e archi adiacenti x₁, a₁, x₂, a₂, ..., x_k−1, a_k−1, x_k, in cui l’arco a_j = (x_j, x_j+1) con j = 1, 2, 3, ..., k − 1 collega il nodo x_j con il nodo x_j+1. Un cammino chiuso è un cammino per cui x₁ = x_k. Un cammino è detto semplice se non ci sono archi ripetuti ed è detto elementare se non ci sono nodi ripetuti. Un cammino elementare che contiene tutti i nodi è detto cammino hamiltoniano.

In generale, se il grafo G = (X, A) non è orientato, una sequenza di nodi non necessariamente distinti è detta percorso. Analogamente al cammino, un percorso è semplice se non ha archi ripetuti, mentre è elementare se non ha nodi ripetuti.

☐ In topologia, il termine cammino è in generale sinonimo di arco, applicazione continua dell’intervallo [0, 1] in uno spazio topologico X: l’immagine dell’applicazione è detta sostegno (o traccia) del cammino, i punti x₀ e x₁ di X corrispondenti a 0 e a 1 si chiamano estremi del cammino, il quale si chiama cappio se tali estremi coincidono. Quando X è lo spazio euclideo ordinario, si parla usualmente di curva (continua a intervallo base finito).