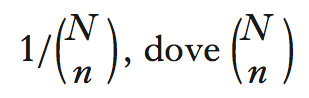campione statistico

campione statistico

Gruppo di unità elementari che formano un sottoinsieme della popolazione. Un c. è generalmente costituito in modo da consentire, con un rischio definito di errore, la generalizzazione all’intera popolazione. Data una popolazione, individuata dal valore di una o più variabili sulle unità elementari, è quindi possibile studiarne le caratteristiche sulla base delle informazioni derivanti dal campione. Formalmente, un c. di dimensione n dalla popolazione P è un qualsiasi sottoinsieme di P contenente n unità. Il c. può essere ordinato o non ordinato, con o senza ripetizione. Data una popolazione si possono definire diverse tecniche di selezione dei campioni. A ciascuna tecnica corrisponde un diverso spazio campionario, che rappresenta l’insieme di tutti i possibili c. che possono essere estratti con la tecnica prescelta. A ogni c. è associata una probabilità di estrazione (probabilità di inclusione), che può essere costante o no. Lo spazio campionario, con le relative probabilità di estrazione, prende il nome di piano di campionamento.

Poiché lo scopo del campionamento è quello di trarre informazioni su alcune caratteristiche della popolazione, identificate da uno o più parametri, è necessario che sia definita una opportuna funzione dei dati campionari che permetta di stimarli. Tale funzione è uno stimatore, e un esempio è dato dalla media campionaria o dalla varianza campionaria. In corrispondenza di ciascun c., lo stimatore può quindi assumere valori diversi. Ne segue che ciascun piano di campionamento induce un’unica distribuzione di probabilità, che viene chiamata distribuzione campionaria (➔) dello stimatore.

I diversi piani di campionamento

Tra le tecniche di estrazione campionaria la più nota è quella del campionamento casuale semplice. Un c. casuale semplice di dimensione n si ottiene tramite estrazione con ripetizione di n unità elementari dalla popolazione, ciascuna con uguale probabilità (o densità, quando si tratti di una popolazione infinita). Nel caso di una popolazione di dimensione finita N, è possibile definire il campionamento casuale semplice senza ripetizione, in cui ciascuna unità della popolazione può essere selezionata per appartenere al c. di dimensione n con probabilità

è il coefficiente binomiale e corrisponde al numero di combinazioni senza ripetizione di n elementi estratti da un gruppo di N≥n unità. A ciascuna unità della popolazione è associata una probabilità di inclusione, ossia la probabilità di essere inclusa nel campione. Questa è uguale alla somma delle probabilità di estrazione di tutti i c. che contengono l’unità prescelta. Un piano campionario nel quale ciascuna unità della popolazione ha la stessa probabilità di inclusione si dice autoponderante. Ne è un esempio il campionamento casuale semplice senza ripetizione, nel quale ciascuna unità ha probabilità n/N di appartenere al campione. ● Esistono molti altri piani di campionamento, tra i quali il campionamento casuale stratificato, a grappoli e a due stadi. Nel primo caso si suddivide la popolazione di N unità in M strati o sottopopolazioni, individuate in modo che all’interno di ciascuna di esse le unità siano omogenee rispetto a qualche criterio, dopodiché si estrae un c. da ciascuno strato, con campionamento casuale semplice. Nel campionamento a grappoli, al contrario, la popolazione è suddivisa in sottoinsiemi (definiti da una misura di vicinanza, spaziale o di altra natura), ciascuno dei quali è chiamato grappolo e viene trattato come una singola unità. A questo punto, si estrae un certo numero di grappoli con campionamento casuale semplice senza ripetizione. Il campionamento a due stadi, invece, associa al meccanismo del campionamento a grappolo casuale quello casuale semplice, per cui da ogni grappolo estratto nel primo stadio si estrae casualmente un certo numero di unità elementari.