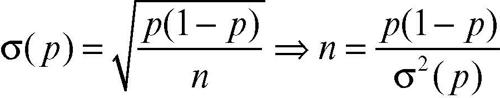campione

campione

campione in statistica, porzione di una popolazione, di cui si registrano uno o più → caratteri statistici, col proposito di ricavarne informazioni sull’intera popolazione; il termine indica anche l’insieme delle osservazioni ottenute da detta rilevazione. La procedura attraverso la quale si effettua la scelta delle unità della popolazione che fanno parte del campione è detta schema di → campionamento. All’operazione di selezione del campione è associato uno spazio campionario, costituito dall’insieme di tutti i possibili campioni che possono essere costruiti dalla popolazione di partenza. Un campione è caratterizzato dai medesimi parametri che contraddistinguono e sintetizzano la popolazione da cui è stato estratto: parametri caratteristici sono per esempio la media e la varianza, dette rispettivamente media campionaria e varianza campionaria, indicate con x̄ e s². Il procedimento attraverso il quale le informazioni ottenute dal campione sono trasferite all’intera popolazione è detto → inferenza statistica. Per determinare l’opportuna dimensione del campione occorre tenere in considerazione la dimensione della popolazione di partenza, l’errore di campionamento, il livello di fiducia e il grado di eterogeneità dell’universo. Inoltre, dalla teoria della stima per intervalli, si valuta che, per aumentare la precisione della stima (diminuendo quindi l’intervallo di confidenza), occorre aumentare la dimensione del campione. La relazione tra la dimensione del campione e la stima si può valutare nel caso specifico della stima di una percentuale. Dalla formula relativa allo scarto quadratico medio della variabile aleatoria “percentuale” di una caratteristica (per esempio, quale percentuale di una popolazione presenti una determinata caratteristica) si sa che:

Nelle formule precedenti p indica la percentuale di unità statistiche che presentano una data caratteristica, σ(p) lo scarto quadratico medio di p e n la dimensione del campione, cioè il numero di unità su cui è stata effettuata la rilevazione. La dimensione n del campione è dunque inversamente proporzionale alla varianza della percentuale. Ciò significa che se per esempio si volesse una stima di tale proporzione con precisione doppia (tale cioè che si dimezzi l’intervallo di confidenza) si dovrebbe considerare un campione quattro volte maggiore. L’aumento della precisione, quindi, si paga con un sensibile aumento delle dimensioni del campione da scegliere: tenuto conto che non sussiste relazione significativa tra il valore stimato e la dimensione della popolazione, da un certo punto in poi l’aumento della precisione, che si paga con un notevole aumento dei costi e dei tempi, non è dunque opportuno o conveniente.