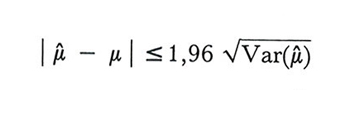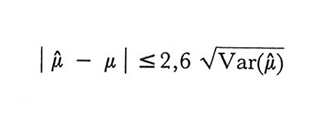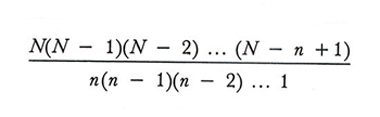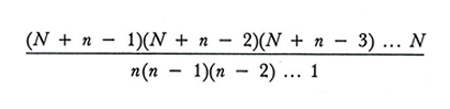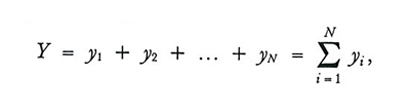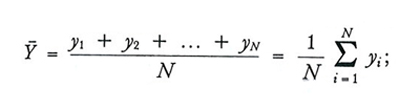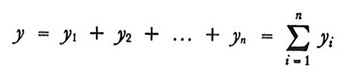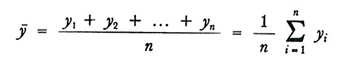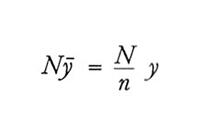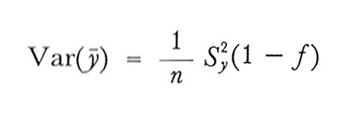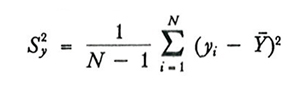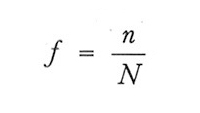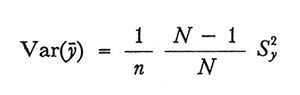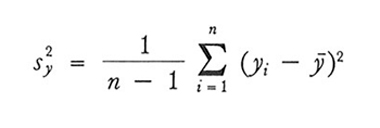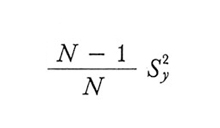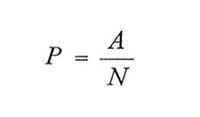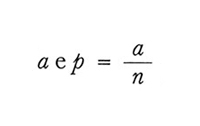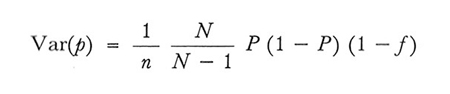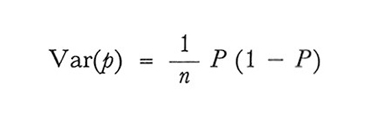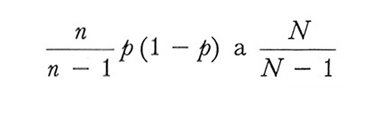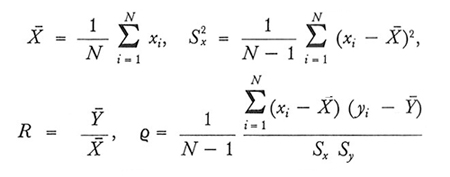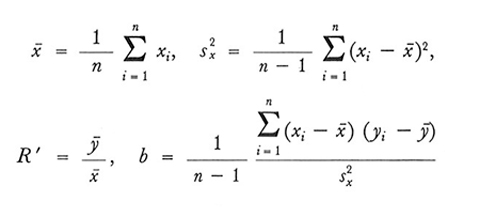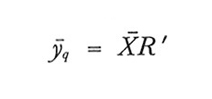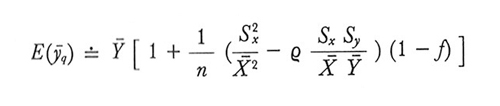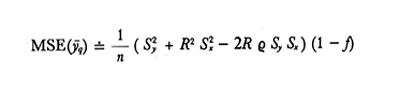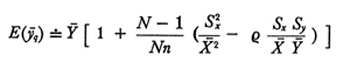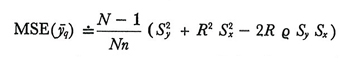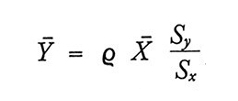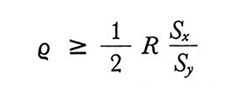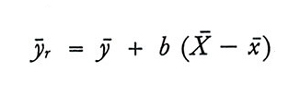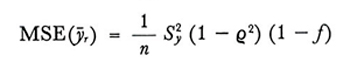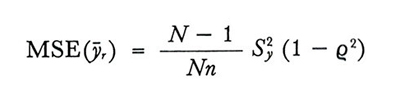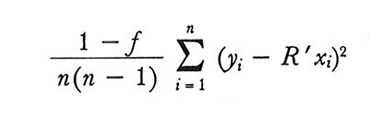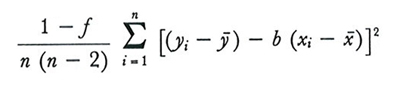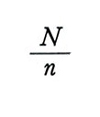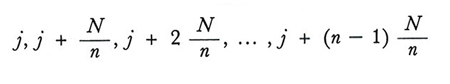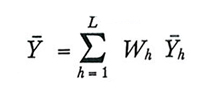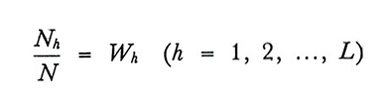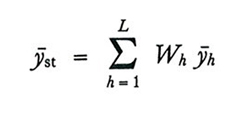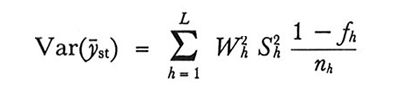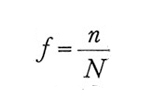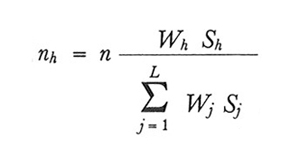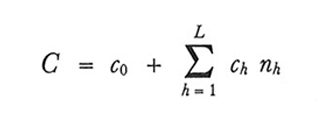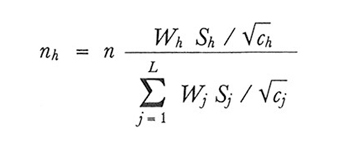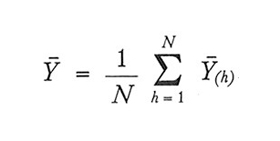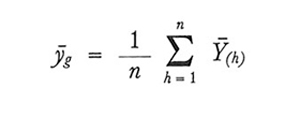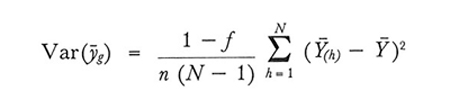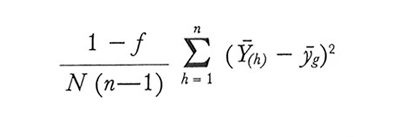Campioni: teoria e tecniche dei

Campioni: teoria e tecniche dei

Introduzione

L'epoca attuale appare caratterizzata, rispetto a quelle che l'hanno preceduta, dal ritmo enormemente più intenso delle evoluzioni e dei cambiamenti, sia in campo sociale, politico ed economico, sia in campo tecnologico e scientifico. D'altra parte, i mezzi di trasmissione e di elaborazione dei dati hanno ormai raggiunto livelli di diffusione e di efficienza fino a poco tempo fa impensabili. Di qui l'esigenza, avvertita in modo sempre più impellente, di disporre di informazioni statistiche abbondanti, varie, approfondite, attendibili e, soprattutto, tempestive.

È oggi generalmente riconosciuto che questa esigenza può essere soddisfatta pienamente soltanto mediante le rilevazioni campionarie, dette anche parziali in contrapposizione alle rilevazioni complete, cioè ai censimenti. I vantaggi del campionamento sono principalmente quattro: 1) la molto maggiore rapidità con cui si possono ottenere le informazioni cercate; 2) la forte riduzione dei costi, dovuta al minor numero delle osservazioni; 3) la maggiore ampiezza e il maggior approfondimento delle informazioni ottenibili, in quanto è richiesto un numero minore di rilevatori ed è quindi possibile impiegare un personale meglio selezionato, meglio istruito e più specializzato; 4) la maggiore accuratezza nella raccolta e nell'elaborazione delle informazioni, sempre a causa del volume di lavoro ridotto che consente un miglior livello qualitativo.

Inoltre la rilevazione campionaria si impone, ovviamente, quando l'osservazione comporta la distruzione delle unità che vengono prelevate (ciò avviene, per esempio, talvolta, nel controllo di qualità).

L'errore 'casuale' che viene commesso nelle indagini campionarie a causa dell'incompletezza delle rilevazioni può essere compensato da una minore incidenza degli errori che per cause varie - comportamento improprio dei rilevatori, reticenza degli intervistati, sbagli nella fase di trascrizione o di pubblicazione dei dati, ecc. - si verificano inevitabilmente anche nei censimenti. Come recenti ricerche hanno messo in luce, tali errori, detti 'sistematici', possono talvolta avere un peso prevalente rispetto a quelli casuali. Si può pertanto dire che, contrariamente a quanto in generale si ritiene, anche sotto il profilo dell'attendibilità non è affatto detto che un censimento sia superiore a un'indagine campionaria.

Queste osservazioni non devono essere interpretate nel senso che i censimenti siano oramai da ritenersi superflui. Essi sono, anzi, spesso necessari per consentire l'elaborazione di buoni piani di campionamento e per utilizzare efficacemente le osservazioni raccolte. D'altra parte si impiegano frequentemente tecniche campionarie per rendere disponibili i dati risultanti da censimenti in tempi considerevolmente più brevi di quelli che sarebbero richiesti dallo spoglio e dalla tabulazione completi. Si può comunque constatare che negli ultimi decenni non solo in Italia, ma in tutti i paesi industrializzati, e anche in molti paesi in via di sviluppo, mentre i censimenti diventano via via meno frequenti, le rilevazioni campionarie si stanno rapidamente estendendo. È facile prevedere che tale tendenza continuerà anche nel futuro.

Elencheremo ora alcuni dei principali elementi che caratterizzano le rilevazioni campionarie e che rappresentano altrettanti problemi pratici che devono essere affrontati nella maggior parte di tali indagini.

1. Obiettivi. È importante definire con precisione, in anticipo, le finalità della rilevazione, altrimenti c'è il rischio di compiere scelte sbagliate.

2. Popolazione. La popolazione è l'aggregato finito di unità da cui viene estratto il campione. Tali unità possono essere individui, famiglie, oggetti, unità economiche o territoriali, ecc. È essenziale distinguere tra la popolazione sulla quale si vorrebbero ottenere informazioni e la popolazione da cui in realtà è possibile estrarre il campione (popolazione campionata): per molteplici motivi (assenze, incompletezza delle liste, mancate risposte, mancanza di rilevatori, ecc.) i due aggregati differiscono sempre, in maggiore o minore misura. Le conclusioni che si traggono dalla rilevazione si applicano, in prima istanza, alla popolazione campionata e dovrebbero essere estese alla popolazione oggetto dell'indagine solo se si può essere ragionevolmente sicuri che non vi siano differenze rilevanti fra le due popolazioni nei riguardi delle caratteristiche osservate.

3. Dati. È importante accertarsi che vengano raccolti tutti e soltanto i dati veramente essenziali, alla luce degli obiettivi della rilevazione. Un questionario troppo lungo fa abbassare la qualità delle risposte anche per quanto riguarda le domande importanti.

4. Metodi di misura e di rilevazione. È possibile scegliere fra diversi strumenti di misura e diversi modi di entrare in contatto con le unità che costituiscono il campione. Per esempio, i consumi familiari possono essere rilevati mediante registrazioni giornaliere a opera degli interessati, o mediante interviste retrospettive; lo stato di salute di una persona può essere accertato con un questionario o attraverso esami clinici, ecc. Di regola i mezzi e i metodi più efficaci comportano un costo maggiore; si tratterà quindi, come avviene per vari altri aspetti delle rilevazioni campionarie, di trovare un accettabile compromesso fra le contrapposte esigenze di precisione e di economicità.

5. Campione pilota. È buona norma saggiare preliminarmente il questionario e il lavoro sul campo mediante una rilevazione su scala ridotta. Ciò permette quasi sempre di migliorare il questionario e può servire anche a mettere in luce difficoltà o inconvenienti insospettati: per esempio può succedere che i costi risultino molto maggiori del previsto.

Per quanto riguarda più in particolare i questionari, che costituiscono, soprattutto in campo sociale, uno degli strumenti principali dell'indagine campionaria (sebbene comincino ora a essere impiegati anche strumenti informatici), rispetto ai contenuti è stata proposta la seguente classificazione: fatti, conoscenze, opinioni, atteggiamenti e motivazioni. Le difficoltà in generale aumentano passando dai fatti alle motivazioni. L'aspetto più delicato della compilazione dei questionari consiste nella formulazione delle domande, per la quale G. Marbach (Le ricerche di mercato, Torino 1988², pp. 206-213) fornisce le seguenti regole empiriche: a) evitare, anzitutto, formulazioni generiche, richieste di opinioni su alternative solo genericamente specificate, terminologie oscure per gli intervistati; b) accertare che situazioni, conoscenze, comportamenti e problemi considerati rientrino pienamente nella cultura degli intervistati; c) rendere il significato di ciascuna domanda univocamente comprensibile a tutti gli intervistati del campione; d) formulare domande che richiedano all'intervistato solo un limitato sforzo di memoria; e) evitare di formulare domande 'orientate', che provocano risposte distorte; f) evitare ogni effetto di imitazione, o risposte che coinvolgano il prestigio o l'autovalutazione dell'intervistato; g) formulare domande che riguardino un solo aspetto e consentano, quindi, risposte omogenee; h) rendere massimo il numero delle risposte univoche; i) disporre le domande in successione ordinata secondo criteri psicologici piuttosto che di contenuto della ricerca; l) limitare le indagini ai temi centrali.

Quanto agli aspetti tecnici, merita un cenno la distinzione tra domande aperte (cioè a risposte libere, non precodificate) e domande chiuse (cioè a risposte preformulate).

Ancora in tema di tecnica delle interviste nelle indagini campionarie, merita un cenno a parte il metodo detto delle 'risposte casualizzate'. Questo metodo può essere applicato quando l'oggetto dell'indagine è di carattere particolarmente delicato (per esempio aborti, evasioni fiscali, consumo di droga, ecc.). In questo tipo di indagini l'intervistato sceglie casualmente, con probabilità prefissata, tra la domanda in argomento e un'altra domanda innocua, senza far sapere all'intervistatore quale domanda è stata sorteggiata, e fornisce la risposta, che deve essere applicabile indifferentemente a entrambe le domande. Successive elaborazioni permettono di ottenere una stima del numero delle risposte riguardanti la domanda sostanziale. Tale schema tende a rimuovere le remore dell'intervistato, in quanto gli fornisce una garanzia supplementare di riservatezza, poiché la situazione personale non può essere individuata con esattezza.

Per quanto riguarda i contatti con l'intervistato, si usano da molto tempo, in alternativa alle interviste dirette, i sondaggi postali e telefonici. Il sondaggio postale presenta talvolta dei vantaggi in termini di costo e consente inoltre di evitare gli errori e le distorsioni dovuti agli intervistatori. Gli svantaggi consistono nella bassa percentuale dei rispondenti e, soprattutto, nell'autoselezione degli stessi. In generale sono necessari ripetuti invii dei questionari, che però possono solo ridurre, non eliminare completamente, il difetto suddetto. Il sondaggio telefonico è caratterizzato anch'esso da un costo inferiore in paragone all'intervista diretta e in generale incontra minore resistenza da parte degli intervistati; inoltre ha ovviamente il pregio della celerità. Gli svantaggi sono costituiti dal notevole peso assunto dagli intervistatori e, soprattutto, dalla differenza strutturale che contraddistingue la popolazione campionata, ossia gli utenti del telefono, nei confronti del resto della popolazione.

Un tipo di campione abbastanza diffuso e che sotto vari aspetti possiede caratteristiche proprie è il cosiddetto panel, termine che indica un campione in cui le stesse unità (individui, famiglie, aziende, ecc.) vengono intervistate o osservate in modo continuativo o a intervalli regolari. Rilevazioni di tal genere (denominate comunemente 'longitudinali') sono ovviamente adatte principalmente a fornire informazioni riguardanti l'evoluzione o i cambiamenti nel tempo di fenomeni dinamici in campo sociale, economico, demografico, sanitario e così via. Queste indagini necessitano spesso di una collaborazione abbastanza attiva da parte degli elementi sotto osservazione (per esempio la compilazione di diari) e comportano quindi un elevato tasso di rifiuti e di autoeliminazioni (soprattutto nelle prime fasi). Inoltre l'esigenza di mantenere inalterata la rappresentatività del campione nei confronti di una popolazione che subisce continue e rapide modificazioni strutturali impone periodiche sostituzioni. Va ancora osservato che talvolta la costituzione di un panel viene originata da considerazioni economiche o tecniche anziché da obiettivi conoscitivi; è questo il caso, per esempio, del panel 'Auditel' composto da 2.300 famiglie, presso le quali l'ascolto televisivo viene rilevato, in modo praticamente continuo, per mezzo di strumenti sofisticati e costosi (meters).

Una questione molto importante è costituita dall'alternativa fra campionamento probabilistico, o casuale, e campionamento non probabilistico. È utile ricordare, a questo proposito, che ancora nel 1926 l'Istituto Internazionale di Statistica, che è l'organismo più autorevole degli statistici a livello mondiale, si mostrò incline a dare la preferenza a un tipo di campionamento non probabilistico, detto 'a scelta ragionata', che consiste nella selezione delle unità che, a giudizio del rilevatore, sono le più 'rappresentative' della popolazione. In seguito, però, questo metodo, come tutti gli altri metodi di campionamento non probabilistici, è stato rigettato sulla base sia di verifiche empiriche che di riflessioni teoriche. È stato mostrato che le scelte dei rilevatori sono spesso influenzate da una molteplicità di fattori imponderabili e possono quindi produrre stime affette da errori sistematici che non sono eliminabili. Ma l'elemento principale a favore del campionamento probabilistico è che quest'ultimo, a differenza dell'altro, consente la costruzione di un ben definito modello matematico e la valutazione, sulla base dei soli dati campionari, del grado di attendibilità delle stime.

Bisogna tuttavia riconoscere che in pratica, per motivi organizzativi o economici, alcune forme di campionamento non probabilistico vengono impiegate tuttora; tra queste ricordiamo il cosiddetto 'campione per quote', nel quale il rilevatore deve scegliere un numero prefissato di unità che rispondono a certe caratteristiche, anch'esse prefissate. Questo metodo è, in pratica, largamente diffuso, perché riduce i costi e accelera i tempi della rilevazione. Tuttavia esso presenta notevoli inconvenienti, in quanto consente al rilevatore di evitare le persone che non si fanno trovare in casa la prima volta e coloro che, per circostanze varie, sono meno facilmente accessibili o pronti a farsi intervistare. È inoltre presumibile che ogni rilevatore abbia la tendenza ad avvicinare, entro le quote che gli sono state assegnate, persone fra loro simili, il che porta a una sottostima della variabilità esistente nella popolazione. Si tratta comunque di un metodo che, non essendo casuale, non consente, a rigore, l'applicazione della teoria dei campioni.

Va segnalato infine che il campionamento non probabilistico ha conosciuto negli ultimi tempi, a livello teorico, una certa qual riabilitazione, sulla base di alcuni modelli detti di 'superpopolazione', nei quali la popolazione oggetto della rilevazione è considerata alla stregua di un campione estratto da una 'popolazione di popolazioni'. Questi modelli presentano un indubbio interesse, ma non hanno trovato finora applicazione pratica, poiché, se non corrispondono alla realtà, possono portare a risultati aberranti, mentre, se sono validi, si possono spesso trovare opportuni piani di campionamento probabilistici (per esempio campioni stratificati o campionamento con probabilità diverse) o metodi di stima (per esempio stime per quoziente o per regressione) che risultano soddisfacenti, senza comportare forti rischi.

La 'teoria dei campioni', nella sua accezione tradizionale, si fonda comunque esclusivamente sul campionamento casuale, nelle sue svariate forme. Più precisamente, questa teoria studia le proprietà dell'insieme costituito da tutti i campioni che possono essere estratti, ossia osservati, da una popolazione data, ma del tutto arbitraria, con un dato piano di estrazione casuale. Sulla base di questo studio, la teoria dei campioni si prefigge l'obiettivo di rendere il campionamento il più efficiente possibile, ottenendo la massima precisione essendo dato il costo o, viceversa, riducendo al minimo il costo compatibilmente con un fissato livello di precisione.

Il principio base sul quale poggia la teoria dei campioni è quello cosiddetto del 'campionamento ripetuto': piani di campionamento e metodi di stima vengono valutati a seconda dei risultati che forniscono quando vengono applicati a tutti i campioni possibili, ossia all'insieme menzionato sopra, che assume la denominazione di 'universo dei campioni' o anche di 'spazio campionario'. Per evitare malintesi è bene ricordare che gli enunciati della teoria acquistano significato solo se riferiti all'universo dei campioni: non riguardano, se non indirettamente, il singolo campione osservato o la stima da esso ricavata.

È utile premettere agli argomenti che verranno trattati in seguito alcune nozioni cui incidentalmente si è già fatto cenno in precedenza. Sia μ un valore caratteristico della popolazione. Viene chiamata stimatore di μ una funzione dei valori campionari, indicata col simbolo μ̂, che viene impiegata per stimare μ. Il valore che la funzione μ̂ assume in corrispondenza di un singolo campione assume spesso la denominazione di 'stima'. La media aritmetica della 'distribuzione campionaria' dello stimatore μ̂, ossia il valore che si ottiene calcolando la stima in corrispondenza di ogni campione dell'universo, moltiplicandola per la probabilità di osservare il campione stesso e sommando, assume la denominazione di 'valore medio' o 'valore atteso' e viene indicato generalmente col simbolo E(μ̂). Lo stimatore μ̂ viene definito 'corretto' se è verificata la condizione

E(μ̂) = μ (1)

per qualunque popolazione. Se tale condizione non è soddisfatta, lo stimatore è detto 'distorto' e la distorsione, B(μ̂), è definita come segue:

B(μ̂) = E(μ̂) - μ. (2)

Osserviamo per inciso che i caratteri latini usati come simboli si spiegano con la loro origine inglese: E sta per expectation o expected value, B sta per bias.

La proprietà di 'correttezza' è importante, ma non è da sola decisiva per la scelta di uno stimatore. In effetti, il criterio di scelta più importante si fonda sulla maggiore o minore variabilità dello stimatore. Difatti, in generale, uno stimatore leggermente distorto ma poco variabile sarà preferibile a uno stimatore corretto caratterizzato da una forte variabilità; ciò in quanto il primo darà luogo a stime che in prevalenza saranno vicine al valore caratteristico che si vuole stimare, mentre le stime indotte dal secondo saranno molto più disperse o, come si usa anche dire, meno stabili. Come misura della variabilità si usa in teoria dei campioni quasi esclusivamente la varianza. La varianza dello stimatore μ̂, che indicheremo con Var(μ̂) è definita come segue:

Var(μ̂) = E{[μ̂ - E(μ̂)]²}.  (3)

Ovviamente, se ^μ è corretto, si trae dalla (3):

Var(μ̂) = E[μ̂ - E(μ̂)²].

Per gli stimatori non corretti si impiega invece l'errore quadratico medio, MSE(μ̂) (dall'inglese medium square error), definito come segue:

MSE(μ̂) = E[(μ̂ - μ)²]   (4)

Si può dimostrare facilmente che sussiste l'identità:

MSE(μ̂) = Var(μ̂) + [B(μ̂)]².

Date le dimensioni dei campioni che in genere vengono impiegati nella pratica, è spesso lecito postulare che gli stimatori seguano con buona approssimazione la distribuzione conosciuta in statistica e nel calcolo delle probabilità come distribuzione normale o legge di Gauss-Laplace. Tale distribuzione dipende da due soli parametri, i cui valori coincidono rispettivamente col valore medio e con la varianza. Ciò permette, se μ̂ è corretto, di affermare, per esempio, che la disuguaglianza

è verificata nel 95% dei campioni, o che la disuguaglianza

è verificata nel 99% dei campioni.

Questi risultati valgono con buona approssimazione anche per gli stimatori distorti, purché il quadrato della distorsione non superi la varianza dello stimatore stesso moltiplicata per un coefficiente dell'ordine di 0,4.

In pratica sarà necessario sostituire nelle espressioni suddette a Var(μ̂), che è sconosciuta, una sua stima.

Il campionamento casuale semplice

I piani di campionamento attualmente usati sono quasi sempre di tipo complesso (stratificati o a grappoli e a più stadi), ma comprendono abitualmente uno stadio (generalmente l'ultimo) in cui si ricorre al campionamento casuale semplice. Inoltre risultati e procedimenti relativi a tale schema elementare trovano utilizzazione diretta o indiretta anche nei piani più articolati.

Il campionamento casuale semplice senza ripetizione assegna a tutti i diversi campioni la stessa probabilità di essere estratti. Se la popolazione, come postuleremo d'ora in poi, è costituita da N unità che si trovano elencate e numerate in un'apposita lista (in pratica la costruzione di simili liste può essere talvolta un compito assai arduo), si procede a una scelta casuale di n numeri interi positivi non maggiori di N, i quali vengono a individuare un campione di n unità distinte. Sarebbe troppo laborioso ricorrere per tale scelta a un meccanismo casuale vero e proprio (come potrebbe essere l'estrazione di palline numerate da un'urna); pertanto ci si serve, a tale scopo, di tavole di 'numeri casuali', ossia di successioni di cifre aventi approssimativamente la stessa frequenza e prive di qualunque forma riconoscibile di regolarità o di periodicità. Tali tavole, che si trovano stampate o che vengono fornite dai computer, in realtà, per la loro natura, sono pseudo-casuali, in quanto non sono il prodotto di operazioni casuali, ma di manipolazioni di numeri irrazionali, accompagnate da verifiche e, se necessario, da correzioni.

Accanto al campionamento senza ripetizione, descritto sopra, si considera anche, ma più che altro in sede teorica, quello con ripetizione, in cui una stessa unità della popolazione può essere osservata nel campione più di una volta, al limite anche n volte. Le formule riguardanti le varianze e i loro stimatori sono più semplici in questo schema; di qui la sua utilità. È inoltre dimostrabile che, se N è grande rispetto a n, come generalmente avviene in pratica, la differenza fra i risultati ottenibili dai due schemi è trascurabile, fino ad annullarsi se si fa tendere N all'infinito.

Il numero dei campioni diversi è uguale a

nel campionamento senza ripetizione, e a

nel campionamento con ripetizione. In questi computi due campioni sono considerati diversi se differiscono almeno per un'unità, senza tener conto dell'ordine dell'estrazione; essi rappresentano quindi, nella terminologia del calcolo combinatorio, rispettivamente il numero delle combinazioni senza o con ripetizione di N elementi di classe n.

Sia D il carattere quantitativo oggetto principale della rilevazione (per esempio la statura, l'età, il reddito, ecc.). Indichiamo coi simboli y₁, y₂, ..., y_N i valori che il carattere assume in corrispondenza delle N unità della popolazione. Parallelamente indichiamo con y₁, y₂, ..., y_n i valori che lo stesso carattere assume nel campione generico. Ovviamente il campione sarà composto solo in casi eccezionali dalle prime n unità della popolazione. Questa considerazione dovrebbe essere sufficiente a evitare equivoci.

Indichiamo con Y e Ȳ rispettivamente il totale e la media aritmetica del carattere nella popolazione:

formula (5)

formula (6)

useremo gli stessi simboli, ma con lettere minuscole, per i corrispondenti valori caratteristici del campione:

formula (7)

formula (8)

Le seguenti relazioni costituiscono alcuni fra i più semplici ma più importanti risultati della teoria dei campioni.

1. Sia nel campionamento senza ripetizione che in quello con ripetizione, ȳ è uno stimatore corretto di Ȳ. In simboli: E(ȳ) = Ȳ. Di conseguenza

è uno stimatore corretto del totale Y.

2. Nel campionamento senza ripetizione la varianza di ȳ può essere scritta

formula (9)

dove

e f è la 'frazione sondata':

Nel campionamento con ripetizione si ha

formula  (10)

3. Si ottengono stimatori corretti delle varianze di ȳ, nei due schemi considerati, sostituendo il valore caratteristico campionario

a S²y nel secondo membro della (9) e a

nel secondo membro della (10).

4. Moltiplicando per N² le espressioni delle varianze di ȳ e dei loro stimatori, si ottengono le corrispondenti espressioni relative allo stimatore di Y.

La (9) permette di constatare che, se f è piccola, il valore di N esercita solo un'influenza trascurabile sulla precisione dello stimatore, contrariamente a quanto si potrebbe ritenere. Per esempio, se n = 1.000 e N = 100.000, si ha Var(ȳ) = 0,00099 S²y ; se N = 1.000.000, Var(ȳ) = 0,000999 S²y : in pratica le due varianze coincidono. La (9) e anche la (10) mostrano, inoltre, che la varianza di ȳ decresce abbastanza rapidamente al crescere di n. Dette formule permettono altresì di constatare che per ottenere uno stesso grado di efficienza le dimensioni del campione devono essere maggiori nelle popolazioni in cui è maggiore la variabilità del carattere oggetto della rilevazione, variabilità che è misurata da S²y.

Partendo dai risultati riportati sopra si ricavano anche le espressioni relative agli stimatori delle proporzioni, o frequenze relative, la cui importanza nelle rilevazioni statistiche è ben nota. Sia A il numero delle unità che nella popolazione cadono in una categoria determinata (per esempio i disoccupati). Sia

la loro frequenza relativa. Indichiamo le corrispondenti frequenze nel campione coi simboli

Si hanno allora le seguenti relazioni.

1. Sia nel campionamento senza ripetizione che in quello con ripetizione E(p)=P.

2. Nel campionamento senza ripetizione

formula (11)

Nel campionamento con ripetizione

formula (12)

3. Si ottengono stimatori corretti delle varianze di p sostituendo l'espressione

P(1 - P) nel secondo membro della (11) e a P(1-P) nel secondo membro della (12).

Non è raro che, accanto al carattere D, oggetto principale della rilevazione, venga osservato anche un carattere ausiliario X̵̵, di cui si conosce la distribuzione nella popolazione. Per esempio, se le unità sono i comuni di una regione, D può rappresentare il numero dei disoccupati e X̵̵ il numero degli abitanti; se le unità sono aziende agricole, D può essere la produzione granaria e X̵̵ la superficie coltivata a grano, ecc. È intuitivamente evidente che le informazioni supplementari fornite dal carattere ausiliario possono portare a stime più efficienti di quelle considerate sopra, purché fra i due caratteri sussista una correlazione abbastanza forte. Queste informazioni possono essere utilizzate per la costruzione di piani di campionamento più complessi, ma anche nell'ambito del campionamento casuale semplice, mediante l'impiego di appositi stimatori di cui si farà ora un breve cenno.

Occorre a questo punto introdurre alcuni altri simboli. Indichiamo con x₁,x₂,..., x_N i valori di X̵̵ nelle unità della popolazione. In altri termini, l'unità i-esima della popolazione è portatrice delle due modalità quantitative yi e xi. Poniamo inoltre:

il simbolo ϱ indica quindi il coefficiente di correlazione lineare di X̵̵ e D nella popolazione.

Per il campione verranno usati i seguenti simboli:

b è quindi il coefficiente di regressione lineare di D su X̵̵ nel campione.

Lo stimatore-quoziente, ȳ_q, è definito come segue:

formula (13)

A causa della presenza della variabile campionaria x̄ al denominatore, non è possibile determinare esattamente il valore medio e la varianza di ȳ_q; tuttavia, se n non è molto piccolo, le seguenti approssimazioni possono essere considerate accettabili.

Campionamento senza ripetizione:

formula (14)

formula (15)

Campionamento con ripetizione:

formula (16)

formula (17)

Dalle formule (14) e (16) risulta che ȳ_q non è uno stimatore corretto, a meno che non sussista l'uguaglianza

ma nella maggior parte dei casi, se n non è troppo piccolo, la distorsione sarà trascurabile. Dal confronto della (15) e della (17) rispettivamente con la (9) e la (10) si ricava che MSE(ȳ_q) ≤ Var(ȳ), e quindi è consigliabile usare ȳ_q anziché ȳ come stima di Ȳ ogniqualvolta sia soddisfatta la condizione

supposto che, come avverrà quasi sempre in pratica, R sia positivo.

Un altro stimatore di Ȳ nel quale vengono utilizzate le informazioni fornite dalle x_i è lo 'stimatore-regressione' ȳ_r così definito:

formula (18)

Al pari di ȳ_q anche ȳ_r è uno stimatore distorto, ma anche in questo caso la distorsione può spesso considerarsi trascurabile. Inoltre si ha sempre MSE(ȳ_r) < MSE(ȳ_q) e MSE(ȳ_r) > Var(ȳ). Infatti si trova che, approssimativamente,

formula (19)

nel campionamento senza ripetizione e

formula (20)

nel campionamento con ripetizione.

Le espressioni a secondo membro della (15) e della (19) possono essere stimate, nei grandi campioni, rispettivamente con le funzioni campionarie

e

Anche questi stimatori, peraltro, non sono corretti.

Va segnalato ancora che in pratica il campionamento casuale semplice viene abbastanza spesso rimpiazzato dal cosiddetto 'campione sistematico'. Tale procedimento può essere descritto come segue. Supposto che

sia un numero intero, si sceglie a caso un solo numero, compreso fra

Se questo numero è j, il campione è costituito dalle unità che nella lista della popolazione corrispondono ai numeri

Se l'ordinamento delle unità nella lista è casuale, il procedimento equivale al campionamento casuale semplice. Talvolta è però possibile ordinare preliminarmente le unità in modo tale da ottenere stimatori più efficienti. In questo caso, però, è impossibile stimare la varianza dello stimatore, a meno di estrarre un secondo campione o di introdurre delle ipotesi sulla distribuzione del carattere nella popolazione ordinata.

Il campionamento stratificato

Nel campionamento stratificato la popolazione viene suddivisa in L 'strati', ossia gruppi di N₁, N₂,..., NL unità, dai quali vengono estratti, secondo il procedimento casuale semplice, campioni di n₁, n₂,..., nL unità. Questo tipo di campionamento viene adottato universalmente, sia per esigenze organizzative o amministrative (per esempio, in Italia, per la necessità di ottenere informazioni, oltre che a livello nazionale, anche a livello regionale o, eventualmente, provinciale) sia, soprattutto, al fine di ridurre la varianza degli stimatori.

Indichiamo con Y̅₁, Y̅₂, ..., Y̅L le medie aritmetiche del carattere nei singoli strati e con S²₁, S²₂, ..., S²L i valori caratteristici S²y calcolati all'interno dei singoli strati. Siano ȳ₁, ȳ₂,..., ȳL e s²₁, ²₂, ..., s²L i corrispondenti valori campionari. La media aritmetica della popolazione Y̅ può essere espressa come segue in funzione delle medie degli strati:

dove si è posto

Di conseguenza lo stimatore di Y̅ nel campionamento stratificato sarà dato da

formula (21)

Utilizzando i risultati relativi al campionamento casuale semplice, si trova

E(ȳst) = Y̅  (22)

e, se i campioni sono estratti senza ripetizione,

formula (23)

dove fh è la frazione sondata nello strato h-esimo:

Dalla (23) si desume che la stratificazione è tanto più efficace quanto più omogenei sono gli strati rispetto al carattere oggetto della rilevazione. Al limite, se Sh2 fosse nullo per tutti i valori di h, ȳst sarebbe sempre uguale a Y̅. Questa eventualità è, ovviamente, del tutto teorica. In pratica una stratificazione accurata, basata su caratteri fortemente correlati col primo carattere, apporta tangibili ma limitati vantaggi rispetto al campionamento casuale semplice. Per quanto riguarda la scelta delle numerosità, n₁, n₂,..., nL, indicato ancora con n il numero totale delle unità campionate, n=n₁+n₂+...+nL, vi sono essenzialmente tre possibilità.

1. nh=Whn (h=1, 2,..., L). Ciò implica che fh è costante e uguale a

f = n N. Il campione stratificato così formato è chiamato 'campione proporzionale' e presenta il vantaggio di essere 'autoponderante': lo stimatore ȳst viene cioè a coincidere con ȳ, la media aritmetica semplice delle n osservazioni campionarie, il che comporta un'importante semplificazione dei calcoli.

2. formula.

Sono questi i valori delle numerosità nh che rendono minima la varianza di ȳst. Campioni siffatti vengono talvolta denominati 'campioni di Neyman'. Dall'espressione scritta si desume, più in generale, che nel campionamento stratificato il numero delle osservazioni deve essere maggiore negli strati di maggiore dimensione e caratterizzati da una maggiore variabilità.

3. Se il costo complessivo della rilevazione, C, può essere espresso come segue:

allora la scelta

minimizza la varianza per un costo dato o, viceversa, minimizza il costo complessivo, essendo data la varianza dello stimatore. Si parla in questo caso di 'campione ottimo'.In pratica il campione di Neyman e il campione ottimo non vengono usati spesso, sia perché richiedono la conoscenza delle Sh, di cui in realtà si hanno, al più, valutazioni approssimate, sia perché le rilevazioni campionarie nella maggior parte dei casi vertono non su un carattere solo ma su una molteplicità di caratteri, e un campione che è ottimale per un certo carattere può essere inadatto per un altro carattere. Per questi motivi si preferisce spesso ricorrere al campione proporzionale. Quale che sia la scelta delle nh, comunque, si ottiene uno stimatore corretto della varianza di yst sostituendo nel secondo membro della (23) alle S²h i corrispondenti valori campionari s²h.

Anche nel campionamento stratificato, come in quello casuale semplice, possono trovare applicazione vantaggiosamente gli stimatori-quoziente e gli stimatori-regressione. Ciò può essere fatto in due modi diversi: a) si possono calcolare in ogni strato separatamente le stime-quoziente o le stime-regressione alle medie ·yh nel secondo membro della (21); tali stimatori sono detti 'separati'; b) si possono invece costruire stimatori 'combinati' che hanno la stessa struttura degli stimatori nel campionamento casuale semplice, ma utilizzano le osservazioni dei campioni estratti negli strati, opportunamente ponderate. In generale risultano preferibili i primi, a meno che le nh non siano molto piccole, nel qual caso convengono maggiormente i secondi. Ovviamente, come nel campionamento casuale semplice, gli stimatori di questo tipo sono distorti.

Vi sono dei caratteri di cui si conosce la distribuzione nella popolazione e che sono fortemente correlati col carattere oggetto della rilevazione, ma che non possono essere utilizzati nella costruzione degli strati perché le liste disponibili non consentono di assegnare le singole unità della popolazione negli strati che ne risulterebbero (per esempio, grado di istruzione, posizione professionale, ecc.). Un modo per superare, almeno in parte, questa difficoltà consiste nella 'post-stratificazione': si estrae un campione casuale semplice e si classificano le unità rilevate secondo le modalità di detti caratteri, per trattare poi il campione come se fosse stato stratificato secondo le modalità suddette. Si ottengono in tal modo stimatori corretti che hanno varianza solo leggermente superiore a quella degli stimatori corrispondenti ai campioni stratificati proporzionali secondo i medesimi caratteri. Per esempio, l'ISTAT attualmente applica questa tecnica in qualche rilevazione per i caratteri 'sesso' ed 'età', abbinandola peraltro a una stratificazione vera e propria rispetto ad altri caratteri.

Il campionamento a grappoli

Come nella stratificazione, anche nel campionamento a grappoli le unità della popolazione, dette in questo contesto anche 'unità elementari', sono raggruppate in insiemi più ampi, detti appunto 'grappoli'. Tuttavia, sotto quasi tutti gli aspetti, le differenze fra i due metodi di rilevazione sono profonde.

La prima, importante differenza sta nell'origine dei raggruppamenti: mentre gli strati, in prevalenza, vengono costruiti dagli statistici e sono funzionali alle esigenze del campionamento, i grappoli sono quasi sempre agglomerati fisici, economici o giuridici preesistenti alla rilevazione, di cui ci si serve soprattutto per motivi economici e organizzativi. Per esempio, per formare un campione di individui è più facile ed economico (anche tenuto conto delle liste esistenti) rilevare le famiglie, anziché le persone isolate; è più comodo prendere gli appartamenti in un gruppo compatto di case, anziché sceglierli a caso in tutto il territorio comunale; se le unità sono costituite da giovani in età scolastica, converrà far capo alle scuole, indipendentemente dal carattere oggetto dell'indagine. Operando in questo modo si riduce quasi sempre la precisione degli stimatori a parità di dimensione del campione; ma, d'altra parte, poiché i costi sono notevolmente minori, è spesso possibile aumentare il numero delle osservazioni, recuperando così, in tutto o in parte, la perdita di 'precisione', ossia di 'efficienza'.

Dal punto di vista tecnico la differenza consiste nel fatto che, mentre si prelevano unità da tutti gli strati, solo una parte dei grappoli è compresa nel campione.

La situazione più semplice, che in realtà ben difficilmente può verificarsi, è quella in cui tutti i grappoli comprendono uno stesso numero di unità elementari. Indichiamo con N il numero dei grappoli nella popolazione, e sia M il numero delle unità elementari comprese in ogni grappolo. Il numero totale delle unità elementari nella popolazione è quindi pari a NM. Indichiamo con i simboli Y̅(₁), Y̅(₂),..., Y̅(N) le medie aritmetiche del carattere D nella popolazione. La media aritmetica della popolazione, Y̅, può essere allora espressa come segue:

Se si estraggono con campionamento casuale senza ripetizione n grappoli e se si indicano con Y̅(₁), Y̅(₂),..., Y̅(n) le corrispondenti medie, è ovvio utilizzare lo stimatore ȳg, che non è altro che la media aritmetica semplice delle medie Y̅(h) osservate:

formula (24)

La situazione è del tutto analoga a quella di un campionamento casuale semplice da una popolazione le cui unità sono Y̅(₁), Y̅(₂),..., Y̅(N). Si trova pertanto

E(ȳg) = Y̅

e

formula (25)

che viene stimata correttamente con

formula (26)

Se i grappoli fossero formati a caso, in media il secondo membro della (25) risulterebbe uguale alla varianza di ȳ nei campioni di nM unità (quante sono quelle che compongono il campione) estratti mediante campionamento casuale semplice dalla stessa popolazione. Di fatto, però, i grappoli sono caratterizzati, salvo rare eccezioni, da una omogeneità maggiore di quella che si osserverebbe per effetto del caso. Di conseguenza le medie dei grappoli Y̅(h) sono fortemente differenziate e pertanto la (25) fornisce quasi sempre valori maggiori di quelli che si avrebbero in un campionamento casuale semplice.

Da queste considerazioni si può anche desumere che, mentre nel campionamento stratificato bisogna rendere gli strati il più possibile omogenei al loro interno, nella formazione dei grappoli, nei casi in cui lo statistico vi possa intervenire (ciò avviene talvolta, per es. nelle rilevazioni agrarie), vale l'esigenza opposta.

Di norma, però, le dimensioni dei grappoli non sono tutte uguali, ma diverse, e talvolta anche fortemente diverse. In tal caso si possono adottare per la stima della media Y̅ tre procedimenti differenti: a) estrarre i grappoli con probabilità uguale, senza ripetizione e usare come stimatore una media aritmetica ponderata delle medie osservate nei grappoli, con pesi dati dal rapporto fra la dimensione di ogni grappolo estratto e la dimensione media dei grappoli della popolazione. Tale stimatore è corretto, ma la sua efficienza in generale è bassa, salvo il caso, piuttosto eccezionale, che l'ammontare complessivo del carattere D nei grappoli sia approssimativamente costante; b) estrarre i grappoli come sopra e usare come stimatore la media aritmetica semplice delle osservazioni. Questo stimatore non è corretto, ma se le medie del carattere D nei grappoli sono approssimativamente uguali, la distorsione è trascurabile e l'efficienza elevata; c) estrarre i grappoli con o senza ripetizione con probabilità proporzionali alle loro dimensioni e usare come stimatore la media aritmetica semplice delle medie dei grappoli estratti. Tale stimatore è corretto ed è molto efficiente, al pari di quello precedente, se le medie del carattere D nei grappoli sono approssimativamente uguali.

In pratica si usano di frequente piani di campionamento a due o più stadi. Per esempio, se le unità di primo stadio sono i comuni, si può procedere, nel secondo stadio, a un campionamento di rioni o di blocchi di isolati, quindi, nel terzo, di famiglie e infine di individui. In ogni stadio si possono impiegare varie tecniche di campionamento o di stima, come, per esempio, la stratificazione, il campionamento sistematico, gli stimatori-quoziente, ecc. Si viene a configurare così una vasta gamma di piani di campionamento, tale da permettere allo statistico di affrontare le situazioni più diverse.

Bibliografia

Castellano, V., Herzel, A., Elementi di teoria dei campioni, Roma 1971.

Cochran, W. G., Sampling techniques, New York 1977.

De Cristofaro, R., Rilevazioni campionarie, Bologna 1979.

Hansen, M. H., Hurwitz, W. N., Madow, W. G., Sample survey methods and theory, New York 1953.

Kish, L., Survey sampling, New York 1965.

Raj, D., Sampling theory, New York 1968.

Zanella, A., Elementi di teoria del campionamento da popolazioni finite, Padova 1974.